Un esercizio perfetto per chi ama la geometria e detesta l'algebra. Ciò che si deve fare è solo tagliare, ruotare, traslare e incollare ... peccato che nessuno abbia avuto voglia di provarci. Riassumiamolo come dimostrazione di un teorema.
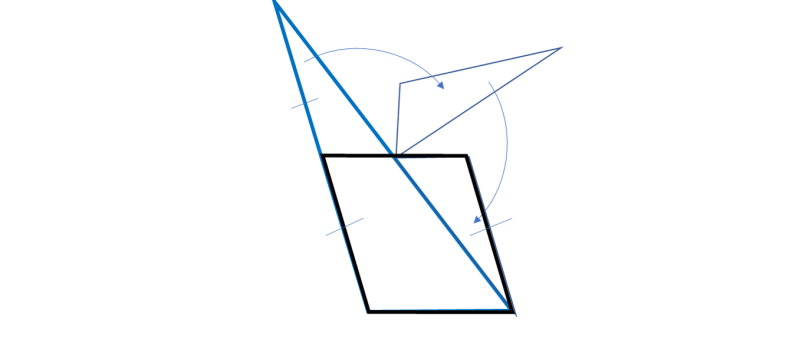

Un esercizio perfetto per chi ama la geometria e detesta l'algebra. Ciò che si deve fare è solo tagliare, ruotare, traslare e incollare ... peccato che nessuno abbia avuto voglia di provarci. Riassumiamolo come dimostrazione di un teorema.

La legge della riflessione luminosa è quanto di più semplice si possa immaginare, eppure è capace di trarre in inganno altrettanto facilmente.
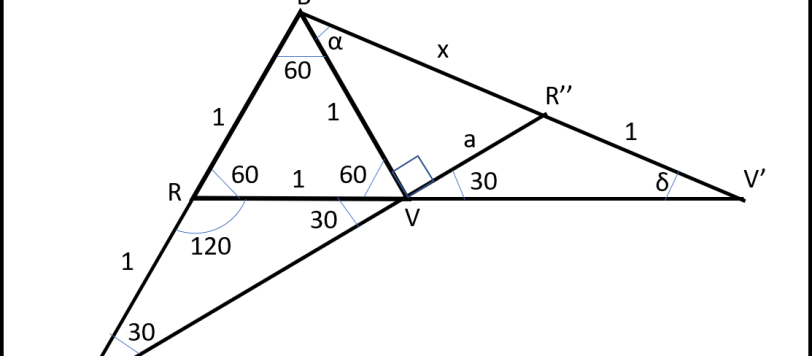
L'esercizio va risolto solo con la trigonometria. Ciò non toglie che alla fine si ottenga un'equazione di quarto grado, la quale, però riesce a essere risolta con estrema facilità. Un bravo a Fabrizio...
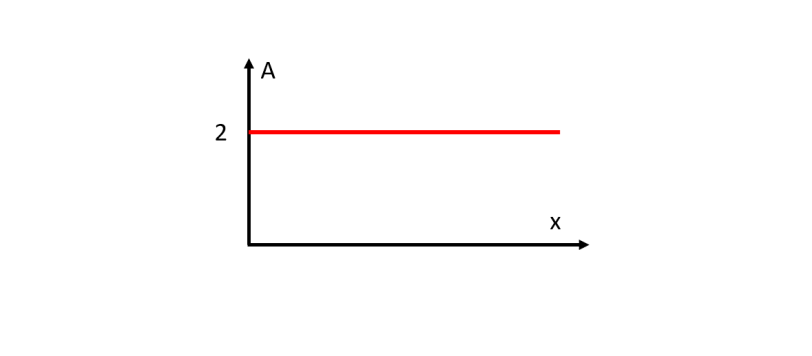
La domanda era poco più che uno scherzo, che Leandro ha subito individuato. Aggiungo la risposta alla domanda di base in modo da ridurre gli spazi...
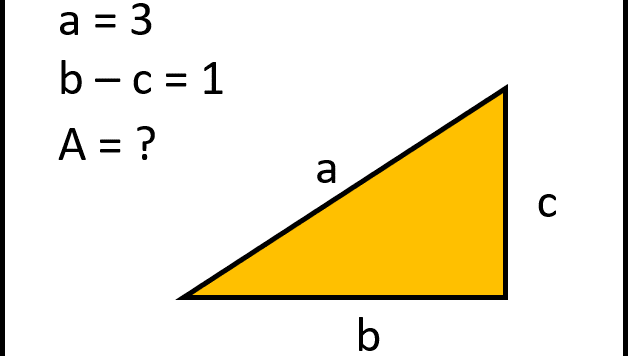
Facciamo divertire anche i meno esperti... Un povero triangolo rettangolo è sicuramente molto intelligente, ma ha appena iniziato lo studio della geometria e della matematica. Gli si fa una domanda che sembra irrisolvibile per la sua limitata preparazione. Riuscite ad aiutarlo?
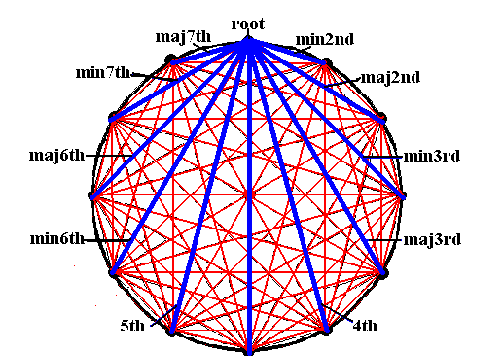
Abbiamo da poco parlato di corde (del cerchio) e di quanto possono essere utili per determinare le aree di figure curvilinee anche molto strane. Nel nostro piccolo, possiamo trovare una relazione tra due corde qualsiasi e la loro corda "media". Una formula semplicissima, all'interno di quella meravigliosa figura geometrica che è il cerchio... Ma voi potreste fare anche di più! Questa volta io mi prendo la parte più semplice e a voi "regalo" la parte più difficile.
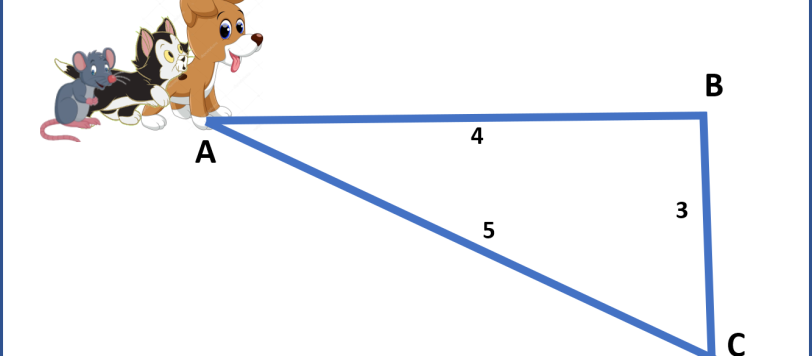
Il problemino sembra subito più difficile di quanto non sia in realtà. Basta ricordarsi che per determinare gli angoli di un triangolo è sufficiente conoscere le dimensioni relative dei lati (come dice Guido).

Qui trovate il quiz e i commenti. Presento la mia soluzione in modo un po' più formale. Questo per dare una spiegazione in più; già leggendo i commenti di Vincenzo (e anche di altri) si riesce a giustificare la soluzione in modo intuitivo-geometrico.Mi baso su una figura, che è un caso semplificato del nostro problema. […]
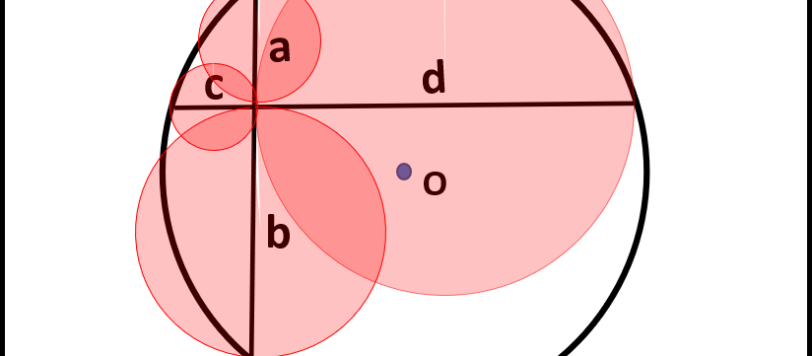
Ecco la soluzione puramente geometrica, anche se, come sempre, il risultato si poteva ottenere in modo analitico.
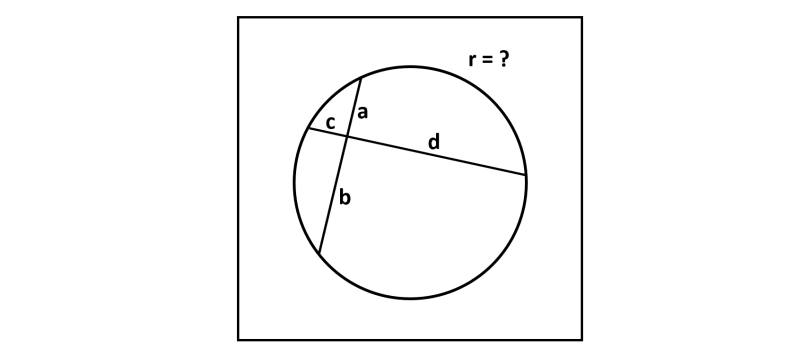
Mentre i più bravi stanno lottando con la molla di Arturo, lasciatemi proporre un semplice (ma non banalissimo) quiz geometrico. Da domani mi prenderò una settimana di ferie rilassanti (soprattutto alla ricerca di funghi) e penso di connettermi poche volte (tutto dipende dai ... funghi). Insomma, ce n'è per tutti i gusti. Prendiamo una bella circonferenza […]

Questo quiz è decisamente semplice, ma, come sempre, deve essere impostato correttamente. Il suo interesse sta nel richiamare un concetto fondamentale della geometria e della fisica.

Un problemino, senza derivate o integrali, che può sicuramente essere risolto in vari modi. Io ho scelto la soluzione che mi appariva più elegante e rapida (da cui i tre asterischi), ma ... qualcuno potrebbe sicuramente superarmi, trovando anche un procedimento più semplice. L'esercizio è stato proposto all'Università di Dublino (ma non tratta di birra...) e lo inserisco per far divertire, almeno, il nostro caro amico Arturo.

Divertiamoci un po' con della geometria semplice semplice. Due quiz relativi a un qualsiasi triangolo, che trovo molto divertenti e stimolanti... Come al solito, un pacco di “niente” a chi propone la migliore soluzione, ossia quella più rapida, con meno formule matematiche (e più ragionamento) e più elegante.
Cerchiamo di risolvere un problemino facile facile solo graficamente. Un certo razzo puntiforme viaggia rispetto a noi che siamo nel sistema in quiete a una velocità di 0.6 c. Vi è anche un altro razzo che viaggia rispetto al primo a una velocità di 0.8 c. Quale sarà la velocità del secondo razzo rispetto a noi? Il problema è facilmente risolvibile con una ben nota formula, ma noi vogliamo provare a risolverlo solo con la geometria...

Avevate pensato di non incontrarli più? Sbagliato! Ecco di nuovo Pippo, Pappo e Peppa alle prese con Nobody, sempre più perverso (malgrado le promesse). Un semplice (ma forse non troppo) problemino di geometria euclidea (finalmente!).