Sono diventati i personaggi del momento... Chi? Loro, proprio quei corpi piccoli, brutti e cattivi che chiamiamo asteroidi. Bene, non c'è momento migliore per costruirne uno in casa nostra!
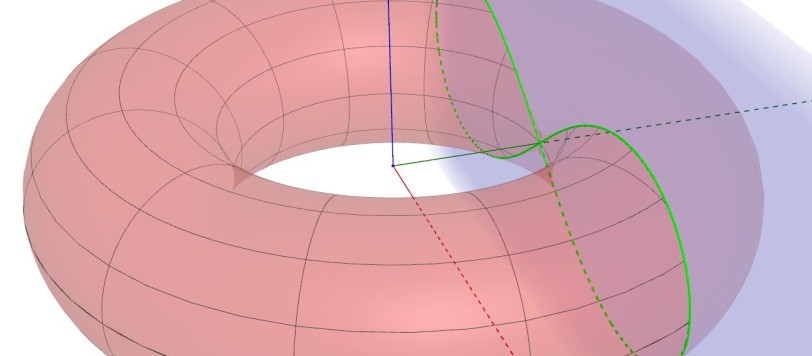
Rieccoci qui con l'ultima parte dell'appendice all'articolo 8° sulla geometria solida, dedicato al toro. Nella prima appendice abbiamo fatto la conoscenza delle circonferenze di Villarceau. In questa seconda appendice illustrerò altre interessanti curve ottenibili andando a sezionare il toro con un particolare piano. Ci serviremo, come sempre in geometria analitica dello spazio, del linguaggio della matematica. Ma niente paura, useremo strumenti semplici. E, in ogni caso, se avete dubbi, non avete che da chiedere nei commenti.
L'ultima volta avevo concluso l'articolo accennando alle sezioni spiriche, che sono proprio quelle di cui ci occupiamo questa volta. Intanto, perché si chiamano spiriche ?
Cominceremo come per un solito quiz, ma poi seguirà un aiutino e infine la risposta. Ognuno si fermi dove preferisce e provi a dare una risposta nei commenti... Aggiungiamo che questo esercizio è alla portata delle scuole medie inferiori, come dimostra l'unico asterisco assegnatogli.
Cosa c'entra il problema che tanto ha assillato, senza successo, gli antichi e puri "geometri" amanti della riga e del compasso con gli elastomeri odierni? Leggete e lo capirete!
Nell'ultima nostra chiacchierata sulle superfici di rotazione ci eravamo lasciati con l'intesa che nella successiva avremmo fatto la conoscenza di una superficie di rotazione che ricorda tanto una ciambella. Eccoci , dunque, qui a parlare del "toro" o "toroide"
Eccoci davanti a due tipici non-quiz. Questo non significa che i solutori abituali dei quiz (sono sempre i soliti noti) debbano sentirsi espropriati del divertimento di provare a risolvere il problema. Possono benissimo riportare le loro soluzioni nei commenti. Proprio per il piacere che trovano a risolvere i quiz (ed è un grande merito) sicuramente non andranno a sbirciare le soluzioni ufficiali. Ormai li conosciamo troppo bene!
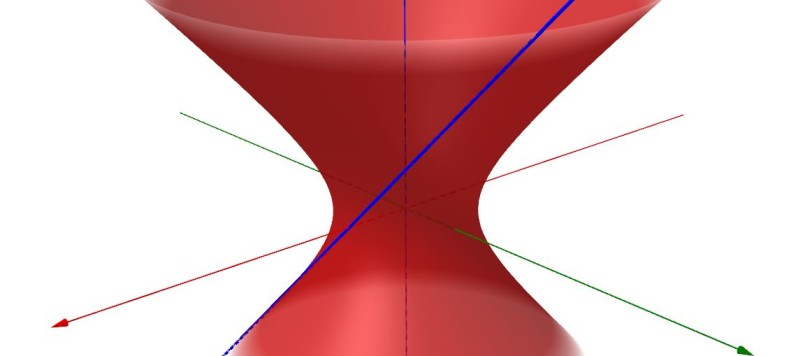
In questo articolo della serie dedicata alle superfici di rotazione ricaviamo la rappresentazione analitica di iperboloidi di rotazione a una falda e a due falde. Possibilità di visualizzare i relativi modelli geometrici, anche in 3D.
Nei commenti potete trovare la soluzione espressa in modi anche diversi tra loro. Noi ci limitiamo a quella -forse- più semplice che necessita delle minime conoscenze dello studio di una funzione.
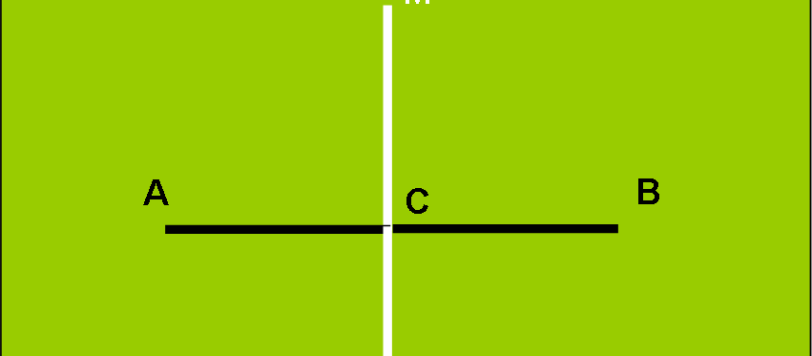
Un quiz matematico-geometrico che potrebbe servire come esercizio in vista dei prossimi esami di maturità. Non un vero problema, ma solo un quesito o poco più…
Pippo, Pappo e Peppa si sono comprati degli appezzamenti di terreno per costruirsi tre casette separate. Purtroppo, la forma totale ABECD non è certo l’ideale per essere diviso equamente.
Ormai sembra proprio che il Prof. Nobody si sia arreso alla intelligenza e prontezza di Peppa, Pappo e Pippo. Tuttavia, ecco che inaspettatamente compare il fratello gemello di Nobody, il Prof. Somebody. Accidenti… lui sembra essere veramente di un altro livello. Questa volta sarà dura per i nostri amici… Cercate di aiutarli!
Questa soluzione si basa sui contributi congiunti di. Arturo, Fabrizio e Maurizio.
Eccoci finalmente a discutere della insidiosa domanda 1C, contenuta nella seconda parte del quasi-quiz sul Monte Cono.
La domanda era questa: 1c) E’ possibile determinare facilmente i semiassi dell’ellisse percorsa per una strada di minimo percorso tra B e B?
Sembrava che il quiz consistesse nel determinare dei semiassi, invece...
Il titolo è sicuramente astruso, ma la spiegazione è semplice. Ho tralasciato a lungo le impressionanti immagini che Juno ha inviato a terra, in attesa di potermi “inventare” qualcosa di speciale (ormai mi conoscete). Ora è giunta l’ora di unire scienza e fantasia, soprattutto dopo tutta la geometria che abbiamo ingoiato attraverso strade su monti conici e le stupefacenti ricerche sulla quadratura del cerchio (e non solo) degli antichi greci.
Torniamo al nostro pi greco che avevamo lasciato al tempo degli egizi. Esso non è ancora giudicato una vera costante, ma il valore di un certo rapporto tra lunghezze o aree. Ma se il pi greco è legato strettamente alla quadratura del cerchio, altri problemi appaiono insolubili per via puramente geometrica.
Nella prima parte del quasi-quiz sul Monte Cono di Papalla, volevamo solo mettere l’accento su quali siano le geodetiche di una superficie conica. Pur essendo estremamente semplici da identificare, possono creare una qualche confusione passando all’atto pratico. Chiariamo bene la loro struttura (rispondendo al quiz) e passiamo a qualche calcolo di minima difficoltà, ma di indubbio interesse.
Si può sciare su Papalla? In un posto solo, dove si erge, nella sua maestosità, un monte conico coperto di ghiaccio e neve, di forma perfetta. I papalliani hanno deciso di costruire, finalmente, una strada per venire incontro ai tanti papalsciatori.