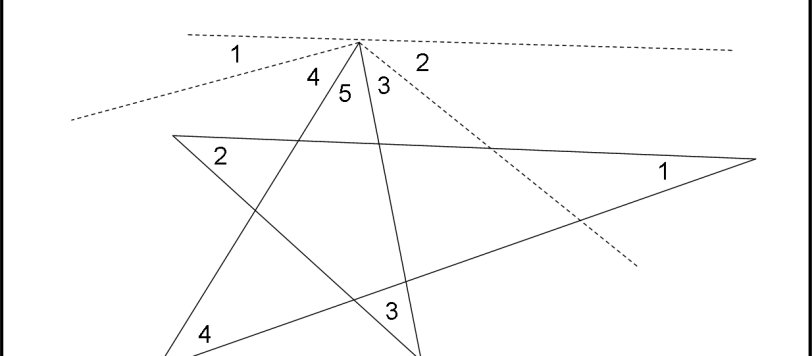
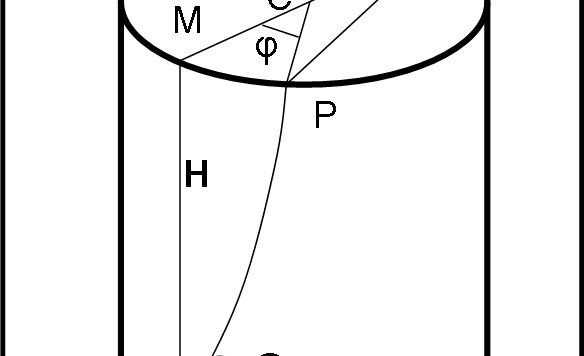
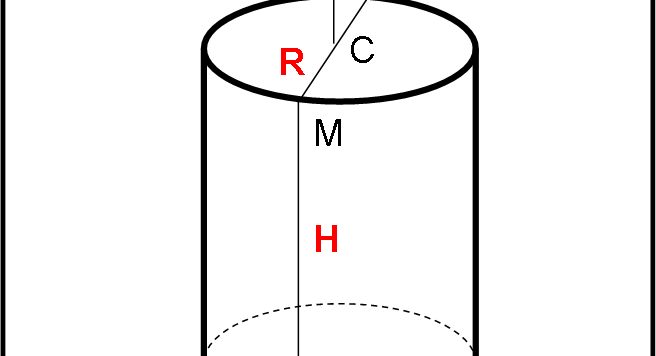
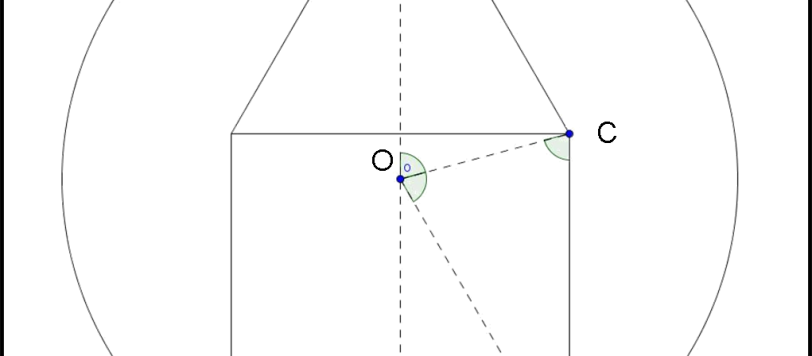
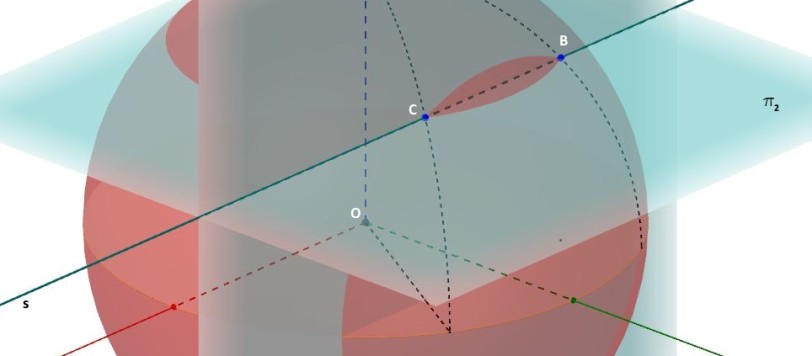
Innanzitutto, come dice giustamente Scherzy (una volta tanto siamo d’accordo… il mondo sta forse invertendo il senso di rotazione?), la risposta alla domanda: “Cosa dovete fare, mentre disegnate la stella, per far sì che la somma degli angoli di tutte e cinque le punte (A + B + C + D + E) sia esattamente uguale a 180°?”. Bene facilissimo… : “Niente!”. A parte, ovviamente, tracciare la linea continua, senza mai fermarsi, e concludere la stella cinque punte. Qualsiasi stella otteniate in questo modo ha SEMPRE la somma degli angoli delle punte uguale a 180°. Vedremo, poi, come Maurizio sia riuscito a generalizzare il problema… Un articolo da leggere, perché è un esempio brillantissimo di come la collaborazione, impostata sul divertimento (e sulle capacità, ovviamente), riesca a dare informazioni sempre nuove e inaspettate.