Un quiz geometrico estremamente semplice che necessita di un minimo di ragionamento. Sia dato un triangolo rettangolo ABC, retto in C. Sul cateto AC fissiamo una lunghezza unitaria AP. Da P tracciamo la parallela a CB che incontra l'ipotenusa AB nel punto R. Consideriamo un punto Q qualsiasi sul cateto CB e sia QB = […]
Cerco di completare questo quiz, anche se sono ancora abbastanza lontano dal riuscire a riprendere adeguatamente la mia attività nel Circolo. Speriamo nelle prossime analisi... Intanto ringrazio Andy per la sua soluzione che mette in evidenza lo stretto rapporto del problema con la sezione aurea e Fabrizio per lo splendido lavoro sulle nuvole che andrà presto a cominciare. A tutti voi un Buon Anno e spero di ritornare presto..
Senza fare troppa fatica, eccovi un quiz... natalizio. Il risultato è molto simpatico.
Non potevo lasciare aperto questo quiz... Grazie a chi ha risposto.
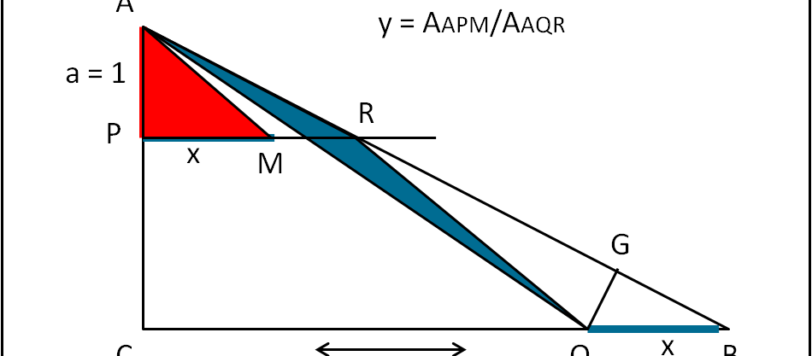
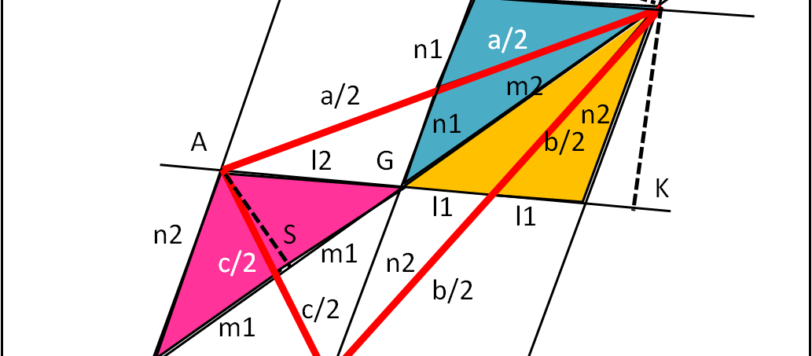
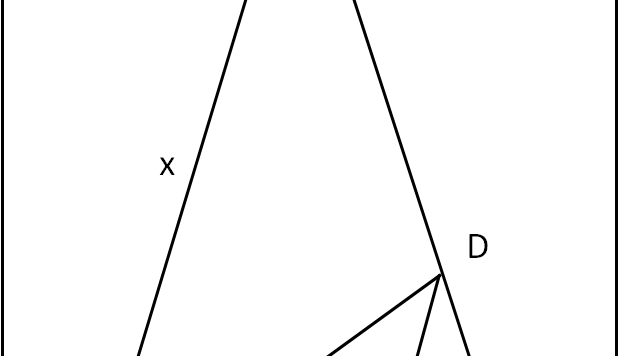
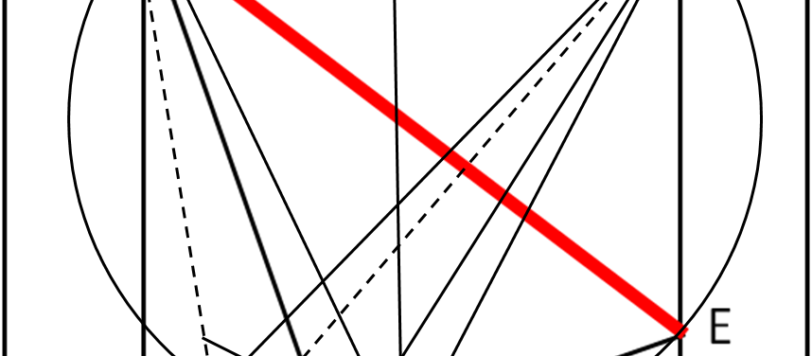
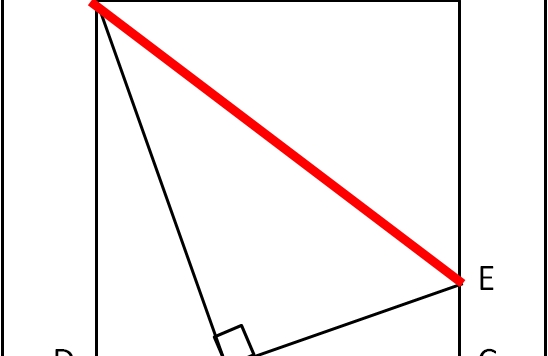
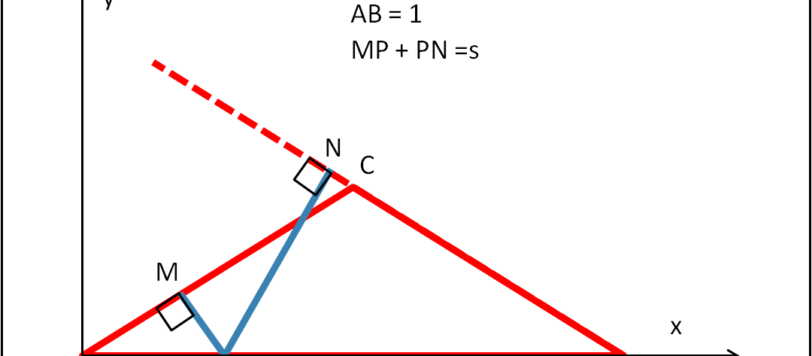
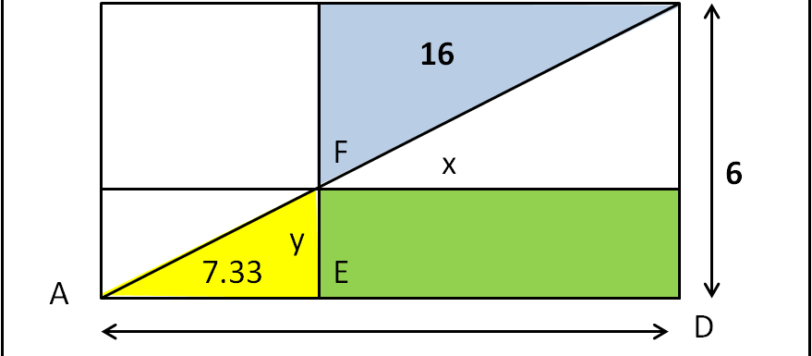
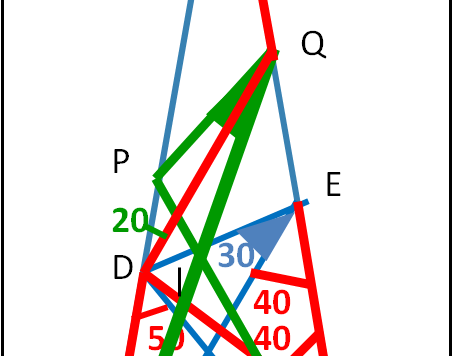
Cari amici, volevo continuare a parlare di nucleo atomico, ma la salute, purtroppo, non è delle migliori e devo fare un sacco di analisi con una certa urgenza. Ne segue che mi manca la giusta concentrazione, oltre che il tempo, per trattare un argomento così delicato e difficilmente semplificabile come la fisica nucleare e la cromodinamica in particolare. Nei prossimi giorni mi dedicherò solo a qualche quiz di geometria, quelli che mi impegnano meno.. I risultati li avrò solo il 27, per cui Buon Natale!
Dopo nuclei che si divertono a rompersi e a unirsi, treni che fischiamo, evoluzione cosmologica, torniamo alla cara geometria (Euclide si è un poco alterato della vostra poca passione a riguardo...).
Un problema presentato alle Olimpiadi di Matematica potrebbe ingannare data la sua semplicità. Attenzione, quindi, a non svolgere calcoli inutili. Bisogna avere il coraggio di dire che è impossibile e dimostrare perché.
Le soluzioni di Maurizio e Andy sono ovviamente giuste (magari completatele...), ma fanno uso dei criteri di similitudine, concetto che non avevo previsto nel testo del quiz. In questo articolo trovate, invece, la soluzione di un quiz estremamente simile, sempre relativo al triangolo 80-80-20, ottenuta senza usare similitudini. Questa soluzione facilmente aiuta ad ottenere anche la soluzione al quiz originario. Volete provare ad aiutarmi?
Ed ecco la seconda parte della soluzione del quiz diabolico olimpico. So che ben pochi la leggeranno... ed è un vero peccato, perché si fa riferimento a diverse importanti caratteristiche dell'unione di triangoli e cerchi. Lo considero un piccolo tributo al grande Euclide.
Come previsto, l'ultimo quiz "diabolico" è veramente complesso e nessuno è riuscito a risolverlo in modo chiaro e geometricamente corretto. Non per niente è stato giudicato tra i più "duri" presentati nelle Olimpiadi Internazionali di matematica. Poco male... Seguiremo insieme una sua soluzione in modo estremamente didattico e scopriremo un teorema poco conosciuto, ma di grande importanza per la geometria superiore. I due asterischi vogliono ribadire che la trattazione che è veramente alla portata di tutti.
Mi allontano per una settimana e propongo questo "regalino" ai più esperti (Andy, Maurizio, Fabrizio, ....) , sperando di non farli annoiare...
Svolgiamo insieme un problema geometrico di cui diamo cinque soluzioni. Magari inizieremo ad amare di più la geometria...
Una soluzione semplicissima a cui ha risposto solo Andy, un super esperto in geometria e non solo.
Torno alla mia cara geometria con un quiz estremamente semplice, che abbisogna solo di colpo c'occhio e un briciolo di intuito. Chissà che non si muovano i meno esperti? I calcoli da svolgere sono proprio alla portata di tutti!
La dimostrazione non è certo semplice. Quasi sicuramente esistono metodi più rapidi ed eleganti. Io non sono riuscito a fare di meglio, ma spero che i passaggi utilizzati siano comprensibili dalla maggior parte dei lettori e stimolino la voglia di partecipare in modo attivo. Magari fornendo una soluzione alternativa che sarà sempre ben accetta!
Nessuna strana relazione e nessun teorema sconosciuto... però la soluzione non è sicuramente banale (almeno quella che riporterò io). Tuttavia, come spesso capita, vi può essere qualche metodo alternativo, più rapido e più elegante...