Un problema che appare piuttosto difficile, ma che, alla fine, si dimostra molto più facile del previsto. Dopo qualche quiz decisamente elementare, presentiamone uno un po' più complicato.
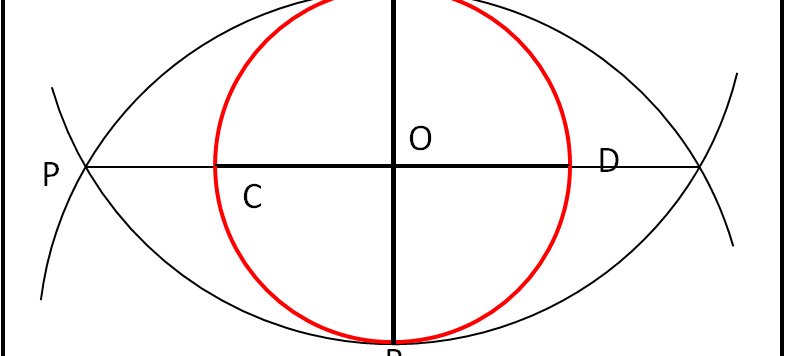
Concludiamo la nostra analisi dei metodi "approssimati" che ci permettono di disegnare qualsiasi poligono regolare di n lati.
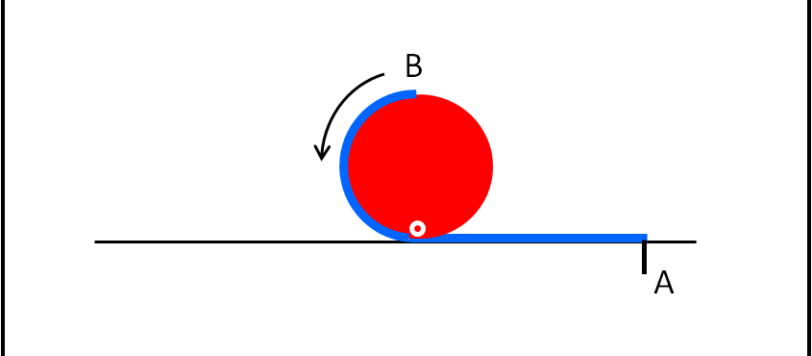
Due monete rotanti riescono a creare più di un paradosso che, però, possono essere risolti e/o prevenuti in qualsiasi caso, senza bisogno di formule.
Questo quiz è veramente facile (lo giuro!). Via libera ai meno esperti...
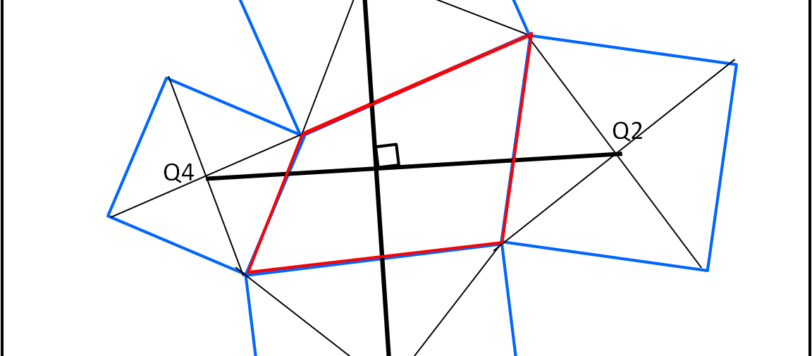
Rinfrescata la memoria sulle proprietà della somma e differenza di vettori, affrontiamo un interessantissimo problema che, nuovamente, potrebbe essere stato enunciato dagli antichi greci. Invito caldamente i più esperti, in attesa del cenone di Capodanno, a tentare di dare la soluzione in modo autonomo, magari indicandomela nei commenti. Vi assicuro che è un bellissimo gico geometrico!
Come spesso accade, le cose più facili possono diventare le più difficili...
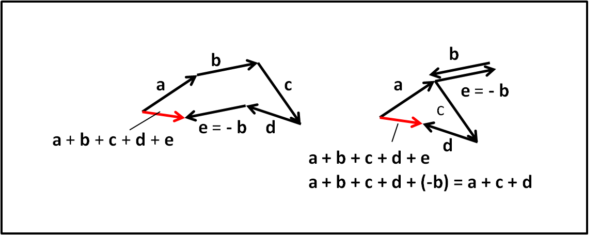
Questo articolo è decisamente elementare e descrive qualche "ovvia" proprietà della somma di vettori. Lo scopo finale, però, va oltre una semplice descrizione, dato che permette di avere le basi per affrontare un teorema poco noto, ma decisamente interessante. Un modo per evidenziare come la matematica e la geometria siano materie tutt'altro che aride e prive di emozioni.
Una nuova avventura di una formica molto affamata...
Ah, questi ingegneri... credono proprio a tutto! Ma è poi vero?
Ancora sulla sezione aurea, ma mettendo in luce un'altra piccola dimenticanza di Euclide & Co.
Guardando una partita di tennis si può ragionare geometricamente, anche se in modo molto "rozzo".
Riprendiamo il nostro cammino nelle rappresentazioni bidimensionali della realtà tridimensionale. Questa volta tocca alla prospettiva accidentale.
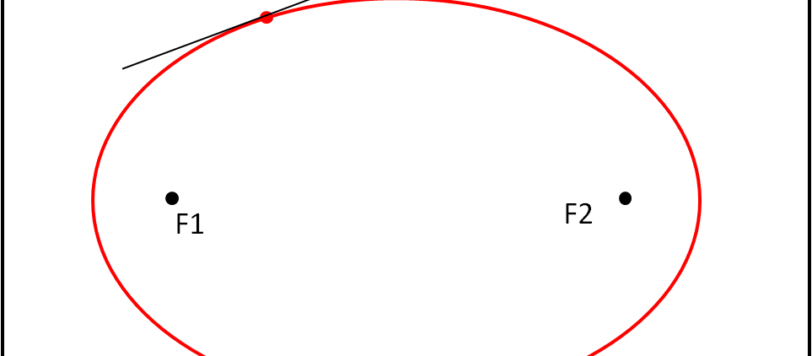
Prima di giocare con un biliardo un po' speciale, fatemi fare una domanda-quiz sicuramente non difficile.
Vogliamo cercare di rendere più semplice possibile il tentativo di gettare un sasso in modo che riesca ad arrivare il più lontano possibile. Per riuscirci, utilizziamo un semplice metodo basato sulla geometria e su un pizzico di fisica classica.
Riprendiamo un argomento che forse è stato trattato in un periodo in cui, giustamente, i nostri lettori potevano finalmente godersi un po' di vacanze.
Il facile quiz sulle taniche da 5 e 3 litri è stato risolto brillantemente da Papalscherzone, ma mi ha fatto venire in mente un modo diverso per arrivare alla conclusione. Tra non molto ci divertiremo con i vettori e allora perché non usarli anche in questo caso?