Quando si tira in ballo il concetto di infinito, si fa in fretta ad avere risultati non banali o intuitivi. Scegliere N punti a distanze reciproche intere e non posti su una stessa retta porta proprio a un problema di questo tipo.

Quando si tira in ballo il concetto di infinito, si fa in fretta ad avere risultati non banali o intuitivi. Scegliere N punti a distanze reciproche intere e non posti su una stessa retta porta proprio a un problema di questo tipo.

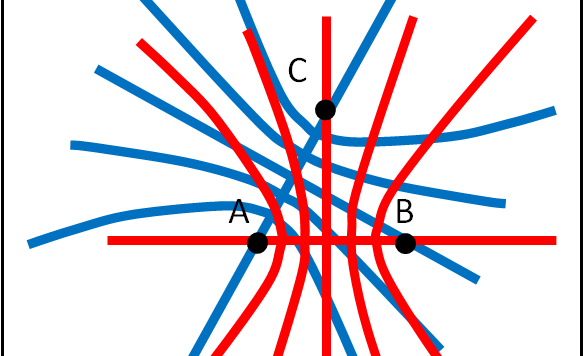
L'infinito sembra irraggiungibile, ma spesso si comporta in modo ambiguo e "scherzoso", dando luogo ad apparenti paradossi. Ne descriviamo uno, facendoci aiutare da un'iperbole equilatera.

Questa è un'altra ciliegina che costruisce uno spaziotempo un po' particolare. Spero che serva ad aiutare e non a confondere... nel caso, ditemelo e la faccio sparire...
Riproponiamo, suddividendola in alcune puntate, la nostra analisi del pensiero e delle opere di Giordano Bruno, ovvero colui che possiamo considerare il vero iniziatore dell'astrofisica e della cosmologia moderna.
Fu, infatti, questo piccolo monaco (ma solo di statura), quando Galileo ancora era poco più che un bambino, a frantumare le "granitiche" sfere di cristallo aristoteliche con la sola forza del pensiero, riuscendo a volare là dove nessun altro arriverà per oltre tre secoli dopo di lui.
L'infinito... amore e odio degli antichi greci. Poteva essere l'insieme di un certa quantità di numeri che non finivano mai o doveva essere trattato come qualcosa di concettualmente non misurabile? Vediamo come Galileo tenta di risolvere uno dei grandi paradossi dell'antichità. Per assurdo che sembri, apre la porta al vuoto, alla caduta dei gravi nel vuoto e al calcolo infinitesimale di Newton e Leibniz.

La libertà di pensiero è il sangue vivo della Scienza!
Questo articolo riunisce in modo organico i quattro già pubblicati su Giordano Bruno, nonché i commenti più interessanti dei lettori, e viene inserito negli approfondimenti.

Continuiamo e portiamo (almeno per ora) a termine il percorso attraverso alcune delle opere più celebri di Giordano Bruno: i tre dialoghi filosofici scritti nel prolifico periodo londinese che racchiudono il cuore pulsante della sua visione cosmologica. In questo articolo, oltre all'opera citata nel titolo, parliamo anche del "De la Causa, Principio et Uno". Buona lettura!

Continuiamo nell'analisi delle idee rivoluzionarie di Giordano Bruno, puntando sui concetti più "azzardati". Lasceremo per ultimi quelli puramente cosmologici che ne fanno il vero precursore dell'odierna Cosmologia. Ci tengo a precisare che nella ricerca di fonti e di richiami è stato fondamentale l'aiuto di Daniela... un articolo decisamente a quattro mani e due menti!
E' arrivato il momento di introdurre il diagramma di Penrose, che ci accompagnerà, con relativa semplicità, a scoprire i segreti racchiusi dentro l'orizzonte degli eventi e, perché no, anche il modo di uscirne. Per adesso, però, impariamo a costruirlo.

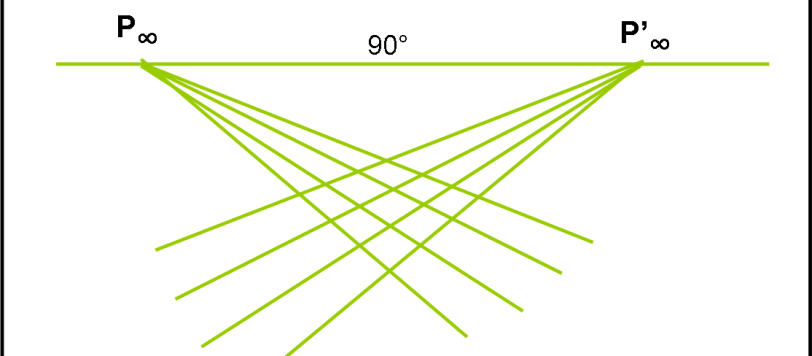
Volevo soltanto chiarire un poco la scelta di argomenti recenti che sembrano piuttosto staccati tra loro, ma che convergono verso un unico punto, in modo simile ai binari paralleli che si incontrano sicuramente nel punto all’infinito. Anche la parola “infinito” non è certo casuale.
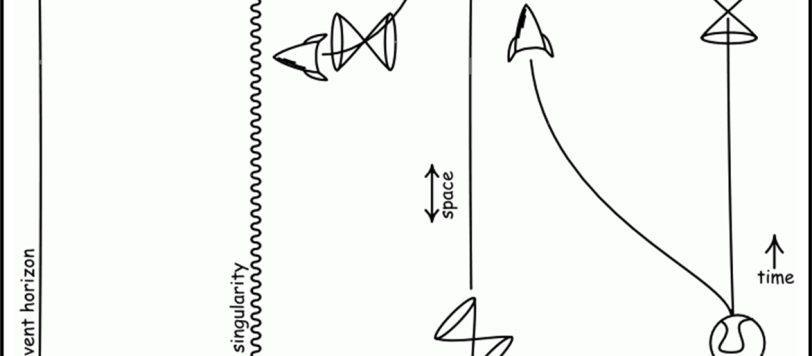
Non è molto che abbiamo descritto un viaggio verso un buco nero. Eravamo arrivati al bordo dell’orizzonte degli eventi, ma non eravamo entrati veramente nelle “fauci del mostro”. E' venuta l'ora di bussare a quella porta che lascia entrare, ma non uscire...

Cosa mai potrebbero avere in comune uno dei più grandi poeti e pensatori di tutti i tempi ed un uomo di Scienza che ha dedicato la propria vita allo studio dell'Universo? Forse poco, forse niente, forse... tutto. Scopriamolo insieme ai nostri teneri ed arguti piccoli amici!
Beh… è bastata l’intrusione di Alvy (era ora!), l’accenno di Umberto e il solito problema di chi parla tanto senza volere prima studiare (non mi riferisco certo a voi!), ed ecco che la frittata è fatta. No, non parlerò di Relatività Generale, ma dell’angoscioso problema del destino dell’Universo e, quindi, della sua “forma”… Attraverso qualche formula che è alla portata di tutti coloro che abbiano digerito la matematica illustrata finora (ma anche meno), ricaviamo nientemeno che la densità critica, data solitamente come risultato di equazioni ben più complicate (ne parleremo quando faremo la relatività generale).
Tempo fa qualcuno di voi, non ricordo se Andrea o Alexander o qualche altro amico, si era posto la questione delle dimensioni di un oggetto. Bene, vorrei azzardare una risposta quantistica.
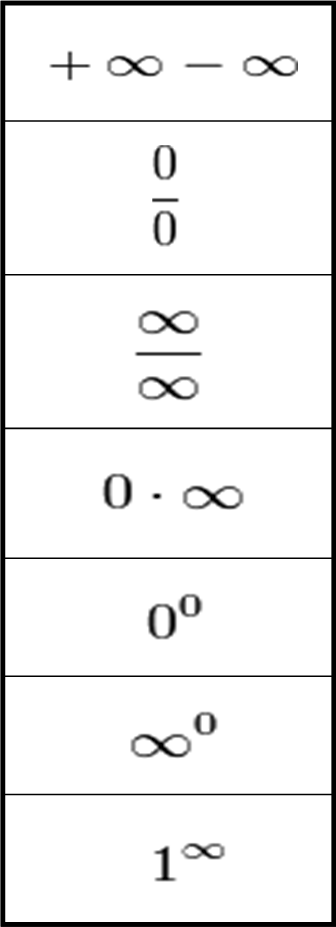
Proviamo ad affrontare operazioni un po’ più difficili, addirittura la moltiplicazione, la divisione e l’elevamento a potenza! No, non ridete. Quando si maneggiano numeri “strani” come infinito e zero le cose non sono mai semplici e regalano molte sorprese. Anzi ci porteranno davanti a un muro che ci obbligherà ad accettare un nuovo approccio.