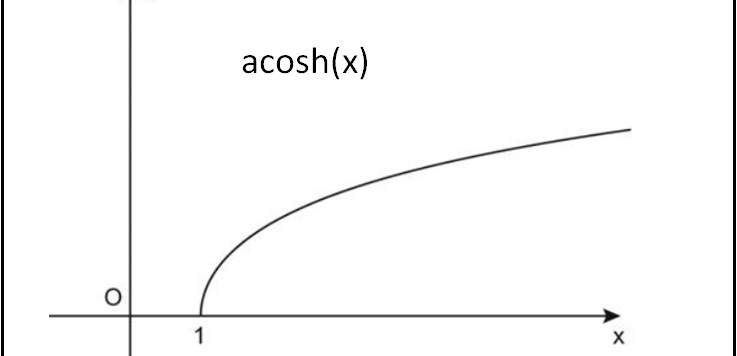
Una breve aggiunta relativa alle funzioni iperboliche e alle loro funzioni inverse.

Fabrizio ha centrato il bersaglio al primo colpo. Durante la prossima nevicata chiederemo consiglio a lui per organizzare la pulizia delle strade!

Un altro metodo piuttosto semplice per integrare qualcosa che sembrerebbe a prima vista piuttosto difficile è quello che comporta una sostituzione di variabile. A titolo di esempio, se abbiamo una certa funzione g(x), potremmo porre t=g(x) e sperare di migliorare la situazione. Ciò che prima appariva come un integrale difficile, si trasforma, magicamente, in un […]

Non ne abbiamo mai parlato, ma questo metodo di integrazione permette di risolvere molti problemi collegati alla soluzioni di integrali che sembrano apparentemente molto difficili, se non impossibili. Ci permette, soprattutto, di proporre quiz piuttosto interessanti e utili.
Come detto, questa serie di articoli vuole essere veramente divulgativa e adatta a qualsiasi livello, sempre che si abbia già un'infarinatura dei concetti di limite, derivata e integrale. Per ottenere ciò, penso che non mi picchierete se a volte sarò ripetitivo e quasi banale. Nella versione definitiva, si potrà sempre cercare di compattare meglio la materia e renderla più uniforme. Per adesso pensiamo ad affrontare nel modo più chiaro possibile i concetti fondamentali.
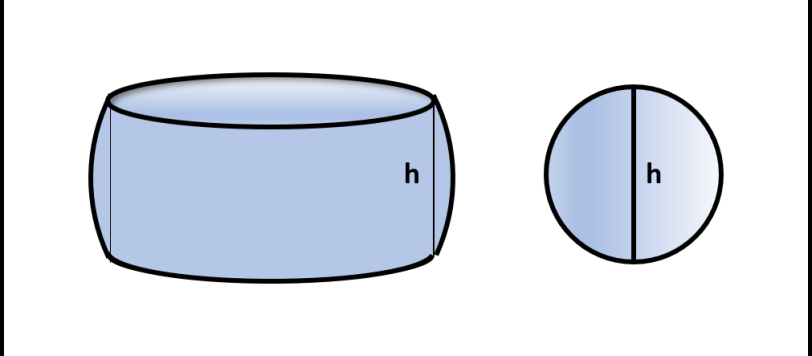
In questo ultimo articolo riguardo a Mamikon risolviamo, con il solo "calcolo visuale" , il problema relativo alla talpa spaziale. Possiamo dire di avere introdotto il teorema di Mamikon ... tridimensionale!

Continuiamo a scoprire le magie di Mamikon e del suo metodo di calcolo visuale. Poi saremo pronti ad affrontare il problema della talpa aliena senza bisogno di nessuna formula che non sia quella del volume di una sfera...
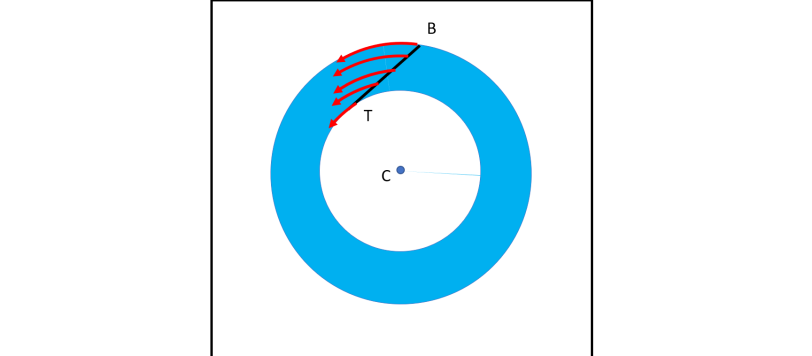
Questo articolo non riporta solo la soluzione al primo di due recenti quiz, ma vuole descrivere molto di più e, quindi, non perdetevelo! La geometria può diventare una specie di romanzo d'avventura... Potremmo chiamarla "geometria dinamica"!

Stupefacente scoperta: i babilonesi utilizzavano le aree per calcolare lo spazio percorso da Giove, proprio quello che abbiamo imparato a fare nelle prime lezioni sugli integrali.
Le derivate comportano sicuramente dei problemi quando le funzioni sono piuttosto complesse. Tuttavia, con un po’ di attenzione e di pazienza, si riesce a portare a compimento l’esercizio. Insomma, le derivate spaventano, ma non poi tanto. Dovrebbe succedere lo stesso con gli integrali che sono l’operazione inversa. E, invece, come tutte le operazioni inverse, le difficoltà crescono di molto. Non è, quindi, assurdo giudicare gli integrali ben più ostici delle derivate. Capita a tutti, anche ai migliori matematici…
Anche se abbiamo concluso (almeno momentaneamente) lo studio delle funzioni, queste ultime rimangono un punto fondamentale della matematica e continuano a essere nel nostro mirino. Vogliamo arrivare al calcolo dei loro integrali e quindi cominciamo con il loro sviluppo in serie, un argomento poco divulgato che è però di importanza fondamentale.
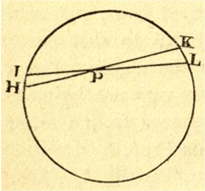
Questo articolo risponde al quiz sul buco della Terra. Ma, in realtà, va ben oltre e ci insegna a valutare sempre meglio la semplice genialità di Newton oltre che darci uno spunto per capire, ancora una volta, cosa s’intende per curvatura spaziotemporale. Questo è il bello della fisica: ogni argomento riesce a collegarsi strettamente a un altro e poco importa se siamo vicini alla Terra o in prossimità di un buco nero. Devo complimentarmi con alcuni di voi (non faccio nomi) che hanno quasi completamente risolto il problema e che, quando ci si sono avvicinati soltanto, hanno mostrato di aver compreso appieno il concetto di fondo su cui lavorare. Le leggi della fisica e la loro eleganza e generalità si imparano un po’ alla volta. Siamo tutti studenti che cerchiamo di aggiungere continuamente un mattoncino alla nostra costruzione, che, se ha le basi solide, non rischierà più di cadere.
In questo file ho inserito tutti gli articoli riguardanti la matematica, dalla conoscenza delle zero e dell'infinito fino alle derivate e allo studio di funzioni. Il linguaggio è quello più semplice e adatto a tutti... Come dice il nostro Paolo: Non serve descriverne i tratti somatici, fissandoli nella propria memoria, la matematica ha bisogno di essere compresa per mostrare la sua semplicità, solo così il brutto carattere lascia il posto al sorriso.