La Lagrangiana sta diventando sempre più necessaria in tutti i problemi di fisica. In fondo, basta compiere la minima... azione!
La massa cresce andando sempre più veloci! Oh, mamma mia, come farò a volare tra le stelle e mantenere la linea?
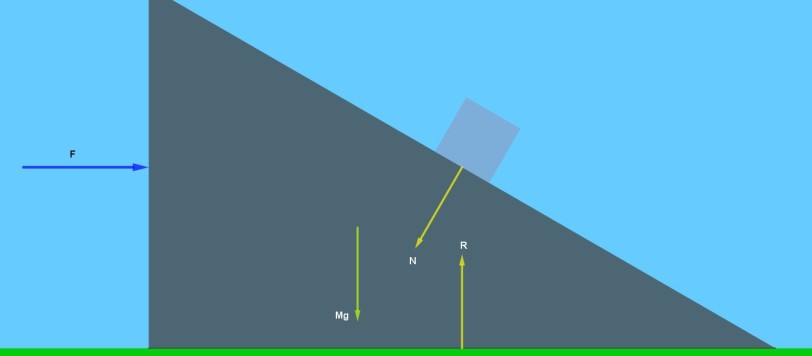
Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica. Questo articolo è partito da un quiz abbastanza semplice e si è poi evoluto attraverso i contributi dati da Arturo e Fabrizio. E' diventato così un piccolo classico, dove abbiamo un cuneo che forma un piano inclinato libero di muoversi senza […]
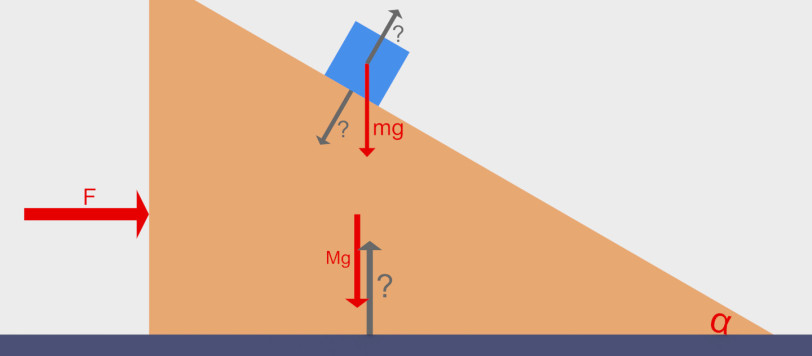
Questo articolo fa parte di una piccola serie dedicata ad un approfondimento sui metodi di soluzione del quiz sul cubo ed il cuneo proposto da Enzo. Questo articolo è dedicato all’applicazione del metodo di Lagrange. L’articolo dovrebbe essere accessibile anche a chi non conosce questo metodo. Per questo accompagno l’applicazione del metodo con una sua breve descrizione.Chi ha avuto la pazienza di leggere la serie di articoli sulla Lagrangiana, potrà trovare qui una applicazione del metodo ad un caso interessante con un riepilogo ed una integrazione degli argomenti trattati negli articoli.
In particolare, questa parte è dedicata all’applicazione del metodo di Lagrange. L’articolo dovrebbe essere accessibile anche a chi non conosce questo metodo. Per questo accompagno l’applicazione del metodo con una sua breve descrizione.
Chi ha avuto la pazienza di leggere la mia serie di articoli sulla Lagrangiana, potrà trovare qui una applicazione del metodo ad un caso interessante con un riepilogo ed una integrazione degli argomenti trattati negli articoli.
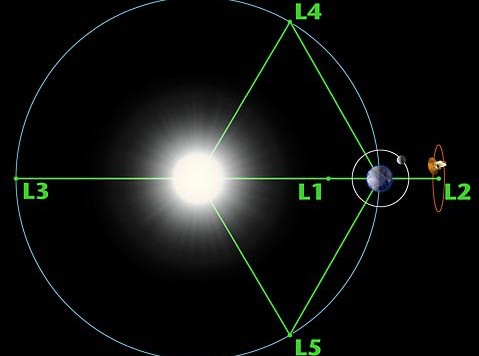
Seguendo gli articoli di Enzo ho notato che citava l'utilizzo della "lagrangiana", per la soluzione di un problema relativo ai punti lagrangiani. Avevo già visto citato questo misterioso oggetto anche da altri che ne parlavano come di una cosa fondamentale nella fisica classica e, ancora di più, nella fisica moderna. A grandi linee sapevo di cosa si trattasse, ma non avevo mai approfondito l'argomento. La citazione di Enzo mi ha incuriosito ulteriormente e ho cercato di capire meglio cosa fosse questa lagrangiana. Questo articolo raccoglie tutti i capitoli usciti a puntate ed è stato inserito negli approfondimenti.
Nelle precedenti puntate abbiamo fatto conoscenza con alcuni esempi di lagrangiana e visto all'opera l'equazione di Eulero-Lagrange su uno di questi esempi. Ora abbiamo tutti gli elementi per tornare al punto di partenza. La frase di Enzo nell'articolo sui punti lagrangiani che mi aveva inizialmente incuriosito: "Per calcolarne l'energia potenziale sarebbe più "fine" usare la Lagrangiana". Ma prima dovremo passare per un esempio di applicazione del metodo di Lagrange ad un sistema non inerziale che finora non abbiamo visto. Ci farà incontrare una vecchia amica che ci inizierà a svelare la frase di Enzo.
Fabricius usa la pietra Lagrangiana per risolvere i problemi. Con la parola magica KappaU li chiude nella pietra che colpita dalla luce Eulgrange emette la soluzione. Noi ci dobbiamo accontentare del metodo di Lagrange che attraverso l'energia cinetica (K) e l'energia potenziale (U) ci fa costruire la lagrangiana. La lagrangiana elaborata con l'equazione di Eulero-Lagrange ci fornisce la soluzione.
Nelle puntate precedenti abbiamo costruito alcuni esempi di lagrangiane di corpi liberi e vincolati ed abbiamo preso confidenza con le derivate che sono utilizzate nella equazione di Eulero-Lagrange.
In questa quinta parte dell'articolo finalmente arriviamo alla equazione di Eulero-Lagrange.
Il viaggio verso l'equazione di Eulero-Lagrange continua.
Occorre fare ancora una tappa per completare la conoscenza delle derivate utilizzate nella equazione.
Come nei gruppi ben affiatati che affrontano i sentieri di montagna, procediamo ad un passo che spero possa permettere a tutti di godere del percorso.
L'equazione di Eulero-Lagrange richiede che siano fatte alcune derivate della lagrangiana.
A prima vista queste derivate hanno un aspetto che potrebbe intimorire, ma dietro l'apparenza non c'è niente di particolarmente difficile rispetto a quelle viste negli articoli di Enzo. Occorre solo farci l'abitudine.
Per iniziare a familiarizzare con queste derivate ho pensato di proporvi questo percorso di avvicinamento alla equazione di Eulero-Lagrange. Strada facendo faremo l'abitudine ad uno degli aspetti che a me ha inizialmente confuso.
In questa terza parte proseguo a proporvi alcuni esempi di lagrangiane. Vedremo alcune lagrangiane di corpi vincolati a seguire delle traiettorie predefinite che mettono in evidenza alcune caratteristiche importanti della lagrangiana e del metodo di Lagrange. Proprio lo studio di questo tipo di problemi ha dato origine al metodo di Lagrange.
In questa seconda parte inizio a proporvi alcuni esempi con i quali ho cercato di esplorare alcune delle forme che può prendere la lagrangiana a secondo del tipo di coordinate e di riferimento che scegliamo. Questi esempi vorrebbero introdurre gradualmente quello che serve per applicare il metodo di Lagrange alla ricerca dei punti lagrangiani.
Gli articoli di Enzo spesso accendono la curiosità verso aspetti della fisica che si incontrano raramente nella comune divulgazione. È successo a me con la Lagrangiana.
In questi articoli metto in comune con il circolo quello che ho capito di questo, per me, misterioso oggetto che è stato concepito da Lagrange più di due secoli fa e che non cessa di avere un ruolo importante nella fisica moderna.
Per impedimenti tecnici non ho potuto caricare l'articolo dal mio account. Ci ha pensato Umberto che ringrazio per essersi gentilmente sobbarcato questa attività.
Cari amici,
In un momento in cui il nostro grande administrator “SMA” è ultra occupato con le feste natalizie e con mille ragazzini alla ricerca del regalo più tecnologico che ci sia, mi permetto di inserire una rapida presentazione di un nuovo brillante acquisto del Circolo, Fabrizio, che già conoscete per i commenti più che puntuali e per aver partecipato alla soluzione della Papalterra.