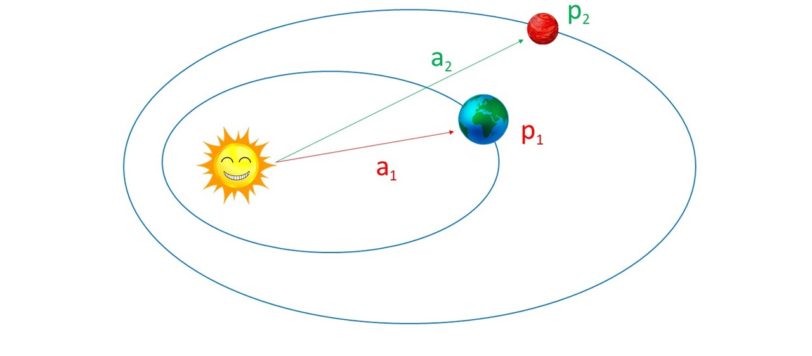
Per parlare del calcolo della distanza Terra-Sole (la cosiddetta Unità Astronomica) non possiamo assolutamente non richiamare il contributo dei grandi scienziati greci.
Questo articolo riunisce le varie puntate relative alla lezione "persa" di Feynman, in cui riesce a ricavare le leggi di Keplero basandosi soltanto sulle leggi di Newton (è stato anche inserito nell'archivio sotto Meccanica Celeste). Il tutto senza nemmeno un'equazione differenziale, ma solo giocando su triangoli uguali e su un diagramma geniale. Una trattazione talmente elegante e semplice che deve essere patrimonio della conoscenza di chiunque abbia vera passione per la fisica.
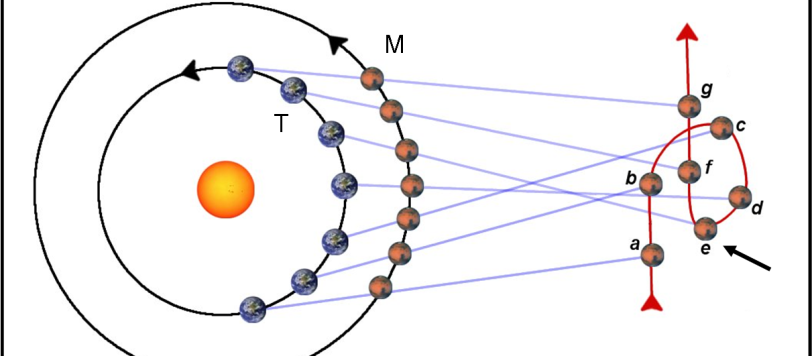
Continuiamo con la storia della determinazione della distanza del Sole, dopo la pausa introdotta con il quiz su Marte, che si rifaceva alla tecnica usata da Cassini. Il solo Paolo l’ha affrontato con grande accuratezza, facendomi pensare che questo argomento sia considerato, per molti, poco importante o interessante. Niente di più sbagliato. Non solo l’esatta determinazione della distanza Terra-Sole ha permesso di definire un’unità di misura fondamentale per qualsiasi approccio quantitativo al nostro Sistema Solare (l’Unità Astronomica), ma la lunga storia che l’accompagna permette di ripassare e di capire meglio tanti concetti relativi alla parallasse, ai transiti, alla trigonometria sferica e alle leggi di Keplero. Un consiglio? Rileggetevi le puntate precedenti e seguite quelle che usciranno. In alcuni casi ci sarà anche l’avventura portata a limiti estremi…
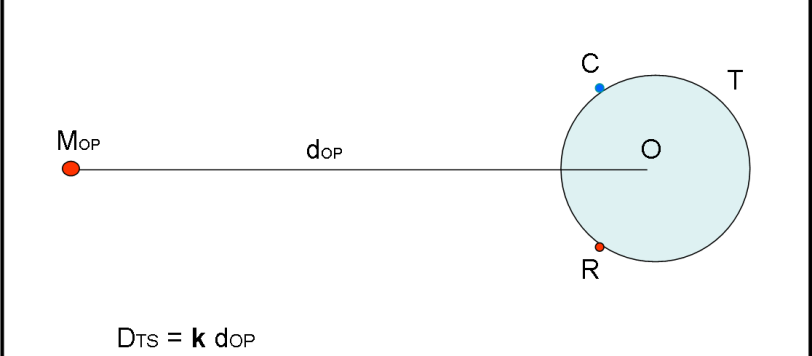
Prima di continuare con la nostra storia della distanza della Terra dal Sole, mettiamoci alla prova con un problemino risolto nel 1672 e quindi di estrema facilità per noi. Tuttavia, vogliamo usare solo ciò che avevano a disposizione a quei tempi. Non andate a cercare nel web dato che troverete sicuramente una parte della risposta, ma, forse, non tutta… Pensateci, quindi, da soli.
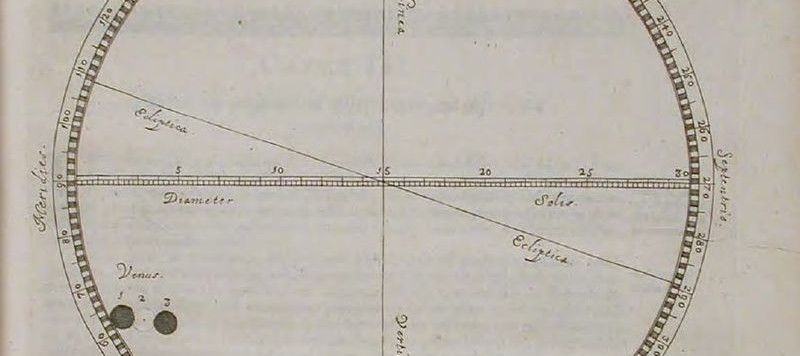
Gli anni passano e insieme a loro anche i secoli, ma la distanza del Sole non è più una problematica interessante. In fondo il Sole gira intorno alla Terra e la sua luce e il suo calore sono opera sicuramente divina. E’, probabilmente, un sacrilegio cercare di misurare qualcosa che è superiore alla limitatezza umana. Con l’avvento della teoria copernicana, però, tutto cambia e la scienza astronomica si scatena verso quello che viene, adesso, considerato un dato fondamentale.
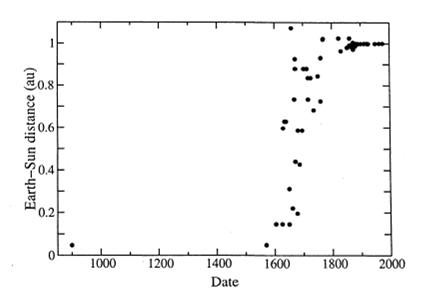
Come si è arrivati alla determinazione della distanza Terra-Sole è una vera e propria avventura che abbraccia molti secoli e che si è risolta solo recentemente. Vale la pena ripercorrerla e analizzare i vari metodi che sono stati usati per ottenerla. Un’avventura astronomica e storica che dovrebbe interessare molti lettori. Iniziamo con una semplice introduzione.
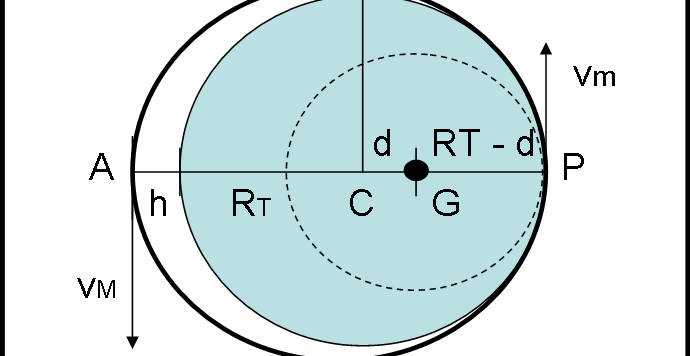
La soluzione che riportiamo è quella dedotta da un’analisi fisica del problema, soggetta a certi vincoli geometrici. La riportiamo, tenendo presente che nei commenti è stata sollevata una soluzione apparentemente migliore, ancora tutta da investigare riguardo alla sua validità fisica. Ricordiamoci che vogliamo inserire un satellite in orbita e quindi impartirgli una certa velocità in un punto ben determinato.
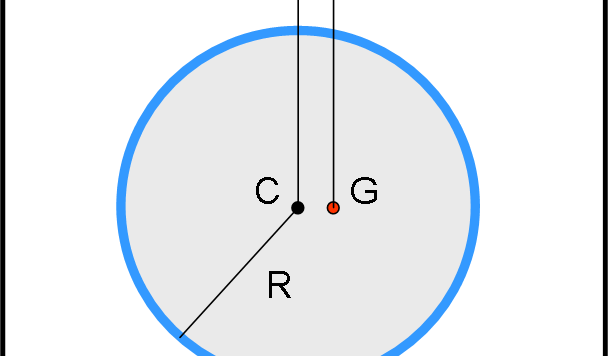
Non si può parlare solo di matematica, di geometria e di giochi numerici ed ecco, allora, un quiz di fisica (meccanica classica), con un piccolo punto chiave. E’ ambientato su Papalla, dove sanno fare cose ancora impensabili per noi.
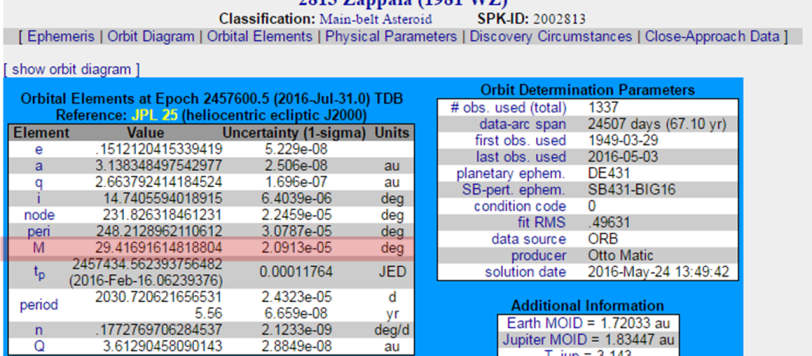
Con qualche difficoltà siamo riusciti a passare dalla legge di Newton alle leggi di Keplero. Ma abbiamo veramente analizzato a fondo le leggi di quest’ultimo? Da loro si ricavano velocità orbitale, si definiscono i parametri orbitali e si introducono nuove grandezze poco conosciute, ma di indubbia importanza culturale. Proprio una di queste ha sollevato la mia voglia di entrare nei dettagli.
Affrontiamo in modo analitico la prima legge di Keplero. Ci accorgeremo che per arrivarci dobbiamo passare attraverso la seconda che acquista non solo un significato fisico ben preciso, ma che ci dimostra che il fatto che l’orbita giace su un piano poteva ricavarsi in modo immediato. C'è tanta matematica, quindi forza e coraggio... ma ne vale la pena!
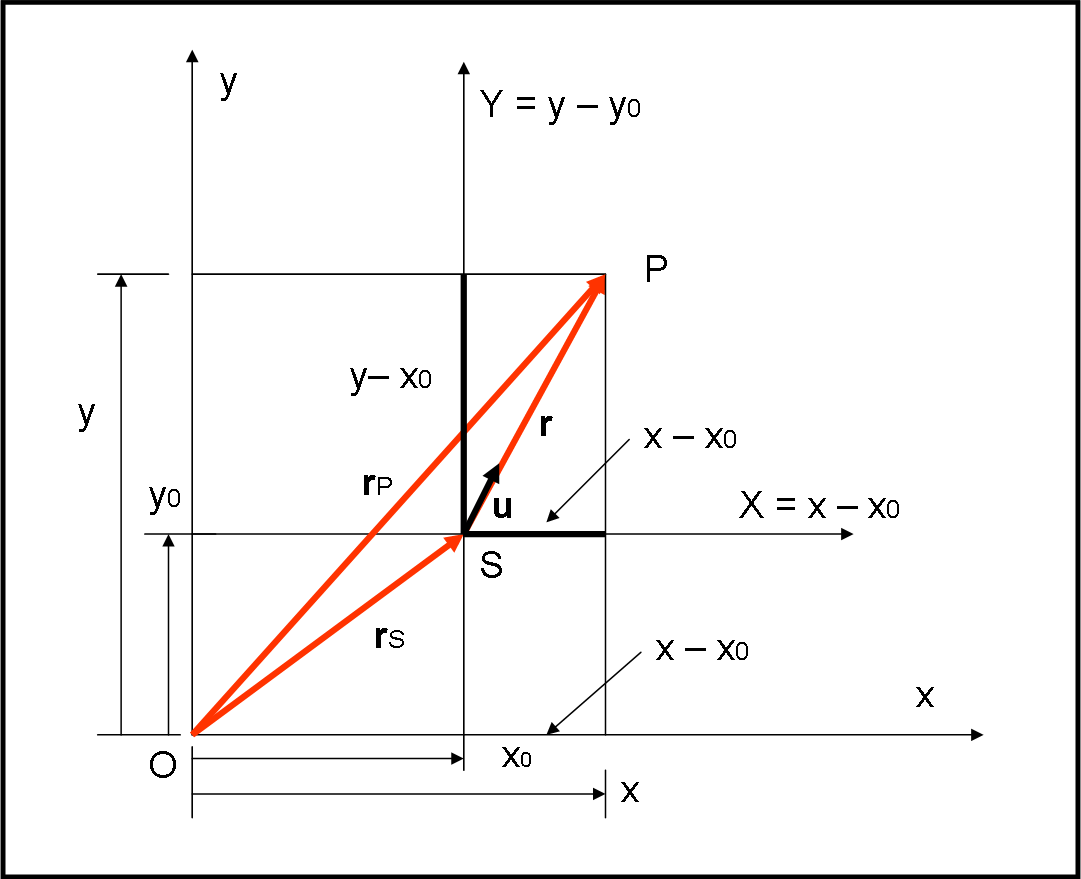
Dedichiamoci al problema più “difficile”, ossia a quello di ricavare il moto ellittico partendo dalla leggi di Newton. Ci accorgeremo che prima di arrivare alla fine, incontreremo già la seconda legge di Keplero, oltre che fare amicizia con un piano. In questa prima parte ci fermeremo proprio su questo piano. Procediamo con molta lentezza e chiarezza. Alla fine il moto orbitale avrà ben pochi segreti...
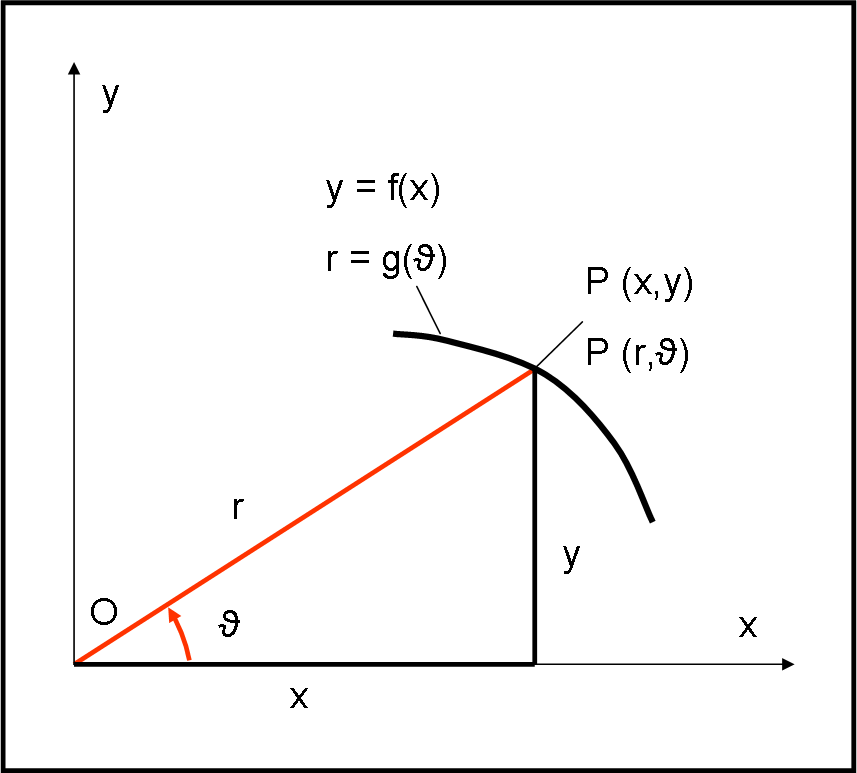
Iniziamo un discorso estremamente importante: partendo dalla legge di Newton vogliamo arrivare alle leggi di Keplero. Può sembrare strano, ma è un argomento trattato raramente, anche se è veramente fondamentale, riferendosi al moto di due corpi. In questo primo articolo ricordiamo le coordinate polari, descriviamo un’ellisse e introduciamo un nuovo tipo di equazione, in modo estremamente semplificato.
Un Natale con la Luna Piena: un’occasione abbastanza rara, anche se non rarissima. Tuttavia, quel tanto che basta per farmi pensare al “faccione” del nostro satellite e proporvi un quiz estremamente facile, ma che spesso viene risolto in modo errato o confuso. Sto parlando delle librazioni lunari…
Questo articoletto riprende il quiz sulle comete di Kreutz proposto qualche giorno fa e a cui è già stata data una risposta molto semplificata. Vediamo di studiare un po’ meglio il moto del Sole all’interno del suo sistema (senza considerare quello ben più ampio e complesso all’interno della Via Lattea e di questa all’interno del suo ammasso locale). La precisazione appare importante, quando si legge spesso e volentieri che il baricentro del sistema Solare è sempre all’interno del Sole. No, non è affatto vero e le comete di Kreutz, che hanno un perielio piccolissimo, ne danno una prova tangibile (se mai ce ne fosse bisogno).
Finora abbiamo ragionato in termini di periodi sinodici (un’utilissima scelta data la loro osservabilità), ma possiamo descrivere gli stessi risultati lavorando con i periodi siderali e con le velocità angolari. Questo approccio ci viene utile per gli allineamenti che escludono il Sole.
La sfera di Hill è particolarmente utile nello studio delle orbite dei satelliti artificiali, dato che pone limiti abbastanza severi per essere sicuri che le perturbazione esterne non causino derive della traiettoria. Anche se si avvicina molto alla definizione di punto lagrangiano, la base concettuale è decisamente diversa. Essa serve per inserire qualcosa in orbita attorno a un corpo che ruota attorno a un altro più massiccio; il punto L1 stabilisce invece un punto di equilibrio tale che un corpo inserito in quella posizione rimanga fermo rispetto al sistema rotante delle due masse principali. Una determinazione accurata è tutto meno che semplice, e ci si accontenta, normalmente, di una approssimazione che risulta del tutto sufficiente se si rimane abbondantemente all’interno della sfera.