Come preannunciato, il quiz sulla quadratura del cerchio era solo una provocazione per introdurre una nuova metrica che si deve nientemeno che a Minkowski.
In questo articolo vedremo la metrica dello spazio-tempo di Minkowski, lo spazio-tempo della Relatività Speciale, ed alcune sue applicazioni.
Questo breve articolo è stato sollecitato da un commento di un nostro lettore che ha escogitato (in modo fin troppo complicato) un esperimento mentale capace di dimostrare che si può superare la velocità della luce. In realtà, vorrebbe dimostrare che la stessa luce riesce ad andare più veloce della luce. Purtroppo, c'è un profondo errore nel ragionamento ed Einstein si salva ancora!
Un esercizio veramente banale per chi ha capito la relatività ristretta e il diagramma di Minkowski, in particolare. Io, come spesso amo fare, lo risolvo in modo puramente geometrico.
L'orologio a luce messo in orizzontale ci dona subito una risposta positiva... ma anche il grande amico Minkowski.
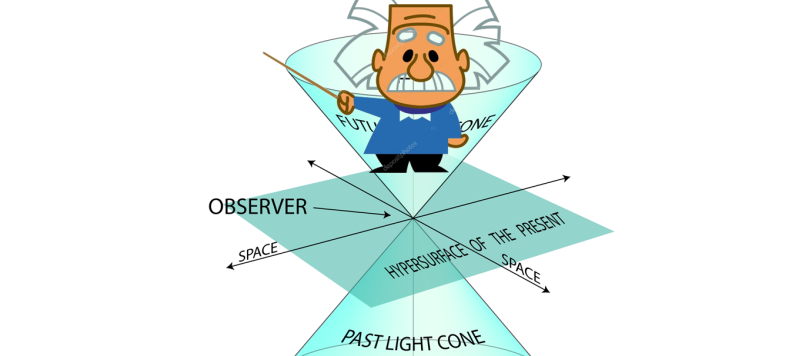
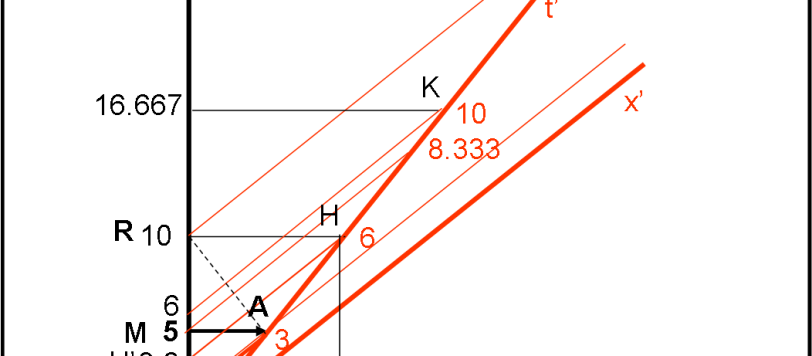
Cerchiamo di risolvere un problemino facile facile solo graficamente. Un certo razzo puntiforme viaggia rispetto a noi che siamo nel sistema in quiete a una velocità di 0.6 c. Vi è anche un altro razzo che viaggia rispetto al primo a una velocità di 0.8 c. Quale sarà la velocità del secondo razzo rispetto a noi? Il problema è facilmente risolvibile con una ben nota formula, ma noi vogliamo provare a risolverlo solo con la geometria...
Un facile esercizio grafico che ci permette di determinare le velocità relative tra particelle (o quello che sono) tra le più agitate dell'Universo: fotoni ed elettroni. Nel riferimento in quiete sta il solito neutrone, pigro come pochi.
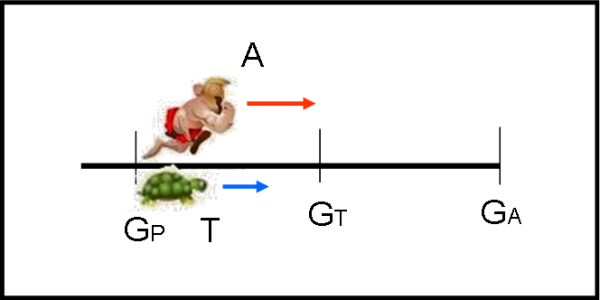
Questo articolo era già apparso, ma il compito dei tre giudici non era stato definito molto bene e ne conseguivano soluzioni ambigue. Ringrazio Guido per avere sollevato il problema. In questa versione credo che i vari compiti siano decisamente ben stabiliti... comunque, se vi sono problemi... parliamone! Con Achille e la tartaruga non si sa mai dove si va a finire...
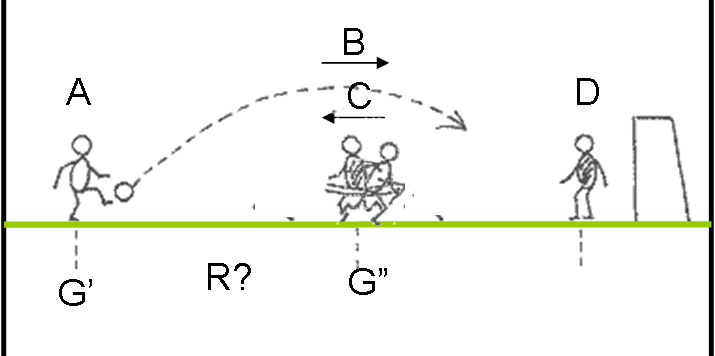
Cosa c'è di meglio di una bella partita di pallone giocata da giocatori "relativistici", ossia capaci di andare a velocità comparabili con quella della luce? Non c'è da stupirsi, però, che ognuno, anche se in completa buona fede, consideri la faccenda in modo diverso... Mi raccomando, non spaventatevi dalle tante domande: basta fare la giusta figura e ogni risposta è di estrema facilità. Comunque, vista la grande sportività che esiste nel mondo del calcio è molto meglio che non si arrivi mai a queste condizioni di gioco: si rischierebbe una vera e propria rivoluzione armata!
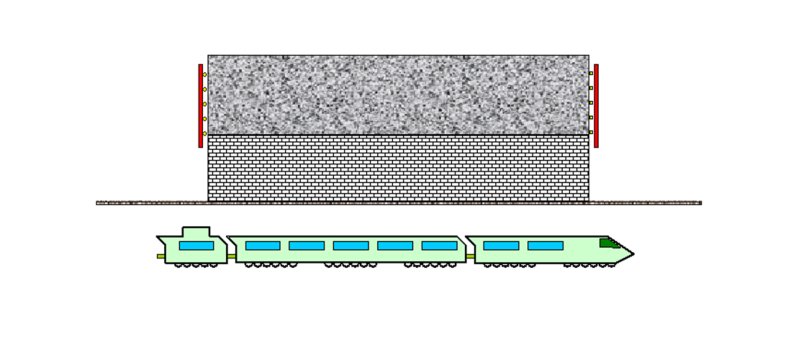
Questo esercizio è veramente un classico per la RR e potrebbe sembrare un paradosso solo a chi non l’ha compresa appieno. Ricordiamo che i fenomeni fisici devono essere uguali in ogni sistema di riferimento, ma non possiamo pretendere che si mantenga la simultaneità dei vari eventi. Un esercizio veramente facile alla portata di molti...
Ho dovuto costruire una storia piuttosto rocambolesca per dare un risvolto pratico a un altro paradosso dei gemelli. Poverini... tutto ciò che succede a loro è sempre paradossale!
Siamo nel 2570 d.C. e un gruppo di turisti si è recato sul pianeta “Paradise” per ammirare la fantastica flora e fauna di quel mondo alieno. L’astronave che li ha portati tornerà a riprenderli molti mesi dopo e si trova a distanza enorme da loro. Ma ecco un fenomeno imprevisto e non certo piacevole per chi sta sul pianeta... non c'è tempo da perdere!
Non voglio sicuramente ricominciare a trattare la relatività ristretta che trova ampio spazio nell'archivio. Tuttavia, avendo visto che lo spaziotempo di Minkowski è l'articolo più letto del nostro Circolo, mi è sembrato giusto tastare un po' il polso dei lettori che l'hanno affrontato. Per far ciò, vorrei presentare qualche esercizio di grande semplicità, ma sufficiente a mettere alla prova le conoscenze raggiunte, soprattutto nelle questioni fondamentali: chiamerò questa serie "Minkowski per tutti". Conoscendo la reticenza dei più nell'uscire allo scoperto, non mi aspetto molte risposte "pubbliche", ma sono sicuro che privatamente molti cercheranno di risolverli. Le risposte si possono ottenere schiacciando su "mostra risposta", ma... chi è relativamente speciale non lo farà di certo!
Un bel problemino relativistico (RR) che sembra portare a un paradosso. Un’attenta analisi dei fatti, però, fa rientrare tutto nelle regole… Einstein , per questa volta, si salva.
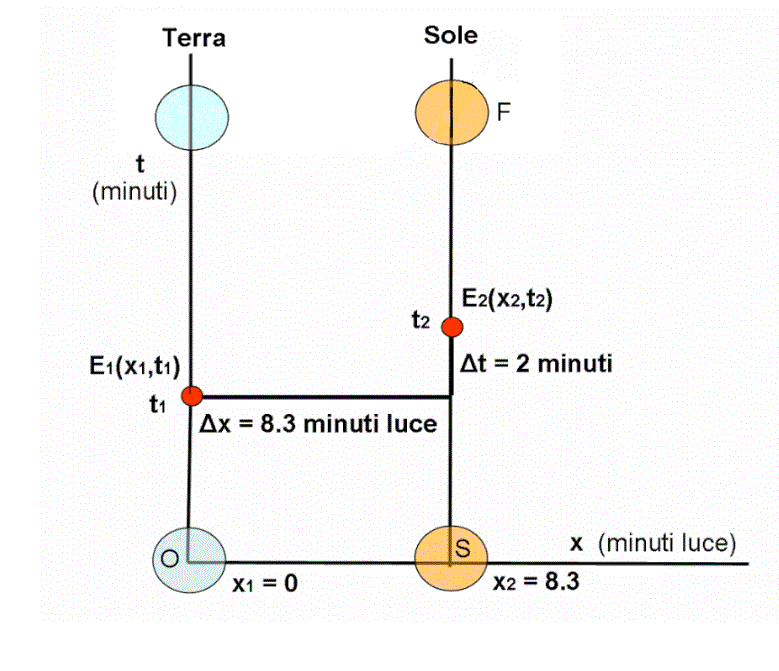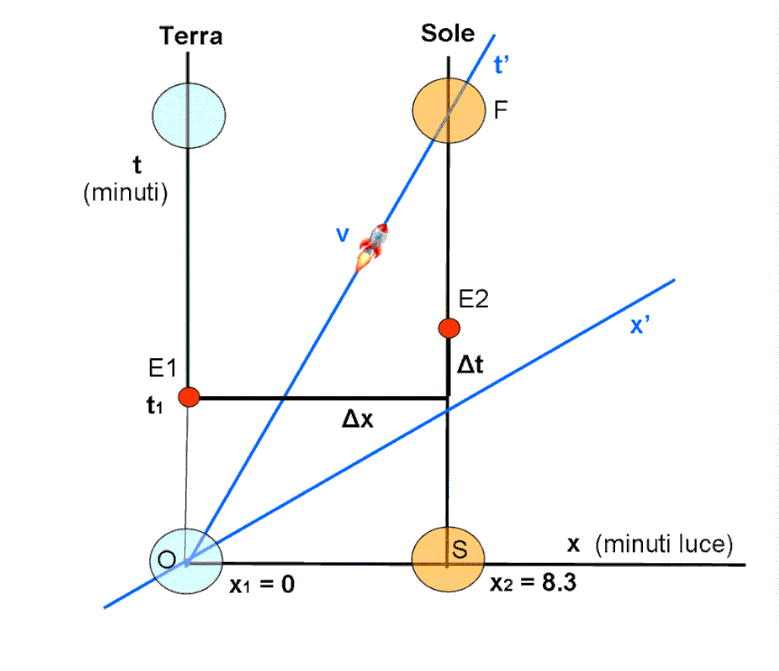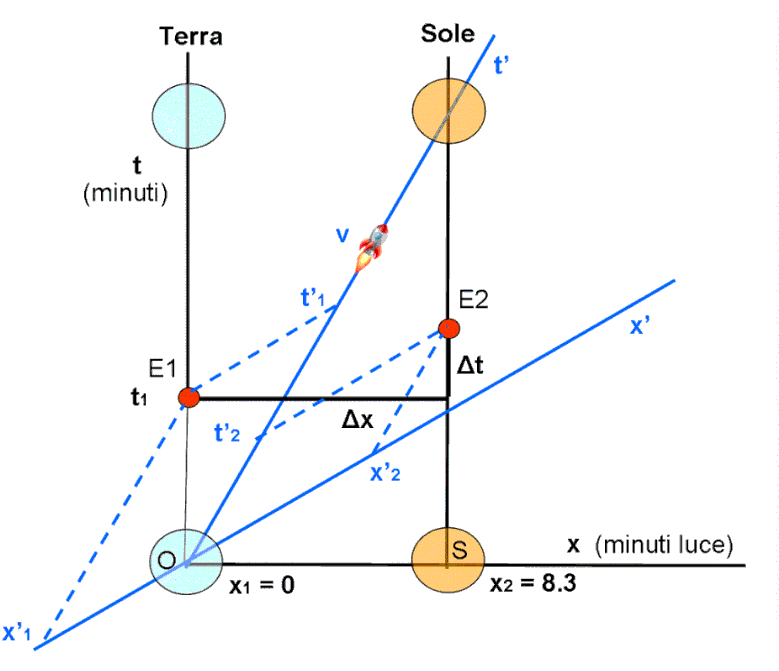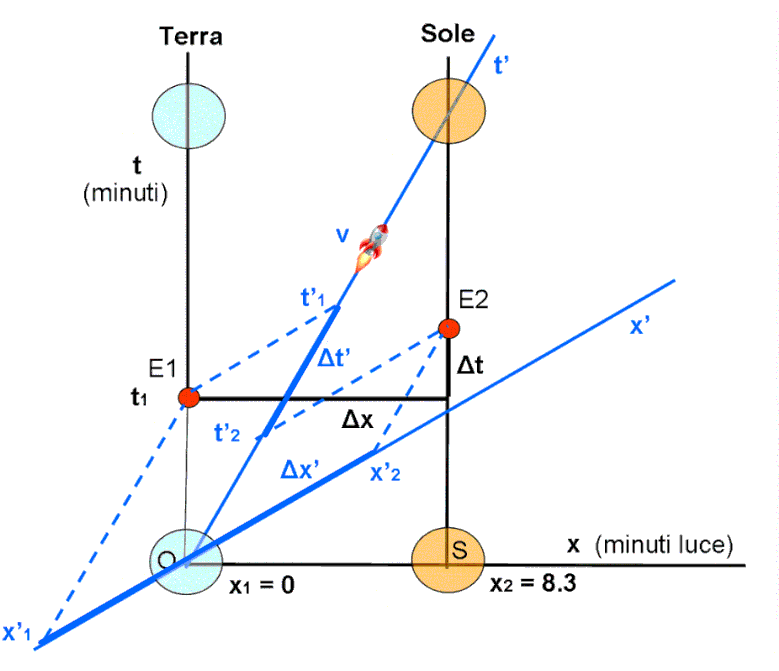
Questo articolo rappresenta la soluzione del quiz sulle esplosioni terrestri e solari, ma è soprattutto una trattazione estremamente didattica (addirittura elementare) che ci permette di calcolare quanto richiesto sia matematicamente che graficamente. La Relatività Ristretta è il filo portante, ma l’articolo segue una linea atta a ricordare. Sarà, perciò, utilissimo per chi ha già studiato la RR, a fare riaffiorare concetti depositati nel cassetto della memoria. Per gli altri, speriamo costituisca uno stimolo ad approfondire la conoscenza di ciò che, in modo sorprendentemente semplice, ha posto le basi per la grande rivoluzione scientifica che sarà la Relatività Generale.
In questo articolo cerchiamo di descrivere, in modo estremamente accurato, le condizioni che accompagnano il paradosso dei gemelli, basandoci essenzialmente sulla relatività della simultaneità e parlando soltanto di eventi. Assumiamo, ovviamente, come già dedotte le trasformazioni di Lorentz per passare da un sistema di riferimento a un altro e la rappresentazione nel diagramma di Minkowski. Abbiamo così in mano tutti i dati per poter risolvere, nel modo preferito, un paradosso che tale, in realtà, non è, ma deriva solo da una violazione della relatività ristretta. In particolare, si dimostra che una soluzione banale e ovvia si ottiene solo con almeno tre sistemi di riferimento (a meno di non passare alla relatività generale, dove il paradosso cessa di esistere).Vediamo, inoltre, come anche altri approcci trattati precedentemente abbiano pari valore e non si discostino molto uno dall’altro.