Dopo aver divagato un poco con il paradosso dei gemelli, torniamo al nostro diagramma di Minkowski e iniziamo a vedere come sia facile ottenere graficamente la dilatazione dei tempi e la contrazione delle lunghezze. Ricordate che è fondamentale aver compreso bene il concetto di relatività della simultaneità e poco altro. Iniziamo con la parte più semplice, quella che riguarda la dilatazione dei tempi.
Con quanto descritto finora, molti di voi sono già sicuramente in grado di determinare graficamente le due più famose ripercussioni della RR: la dilatazione dei tempi e la contrazione delle lunghezze. Senza alcuna formula, però… solo con una matita!
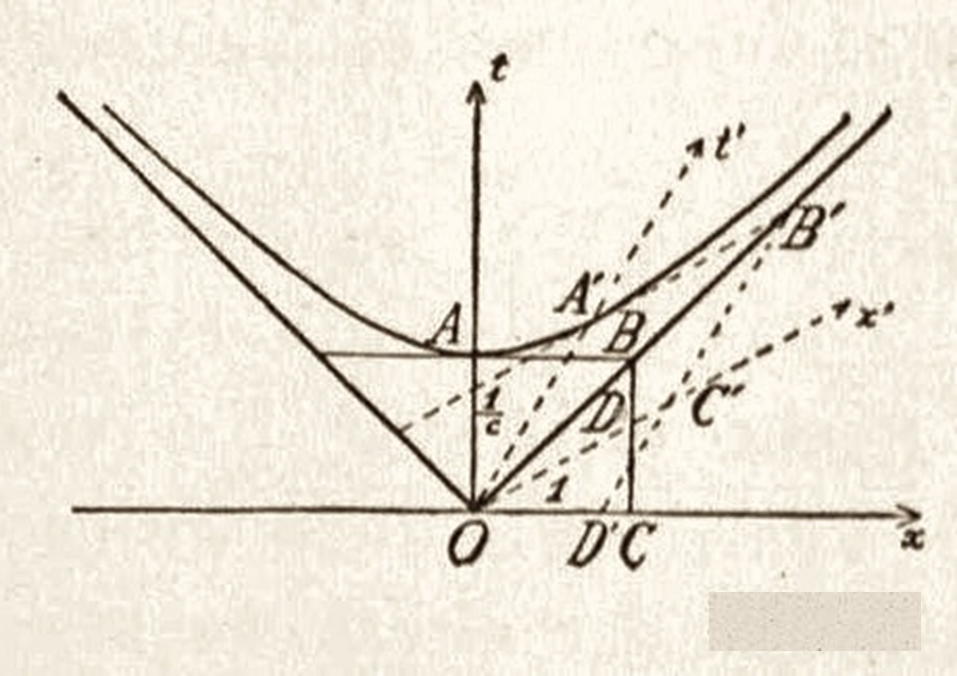
Questo quarto articolo conclude in qualche modo la presentazione del diagramma di Minkowski da un punto di vista puramente geometrico. Viene introdotto l’invariante spaziotemporale e si capisce molto meglio cosa rappresentano le iperboli trovate precedentemente. La dilatazione dei tempi segue quasi automaticamente. Tuttavia, ci fermiamo un attimo prima. L’articolo può risultare un po’ difficile se non si legge con grande attenzione e non si collega continuamente con quelli precedenti. Lo lasciamo un bel po’ in visione in attesa di domande e dubbi riguardanti “solo” lui. Mi raccomando, non cerchiamo di estrapolare in avanti se no si rischia veramente di confondere i meno preparati. Lo scopo ultimo deve essere quello di regalare a TUTTI la RR e non provare la capacità di pochi…
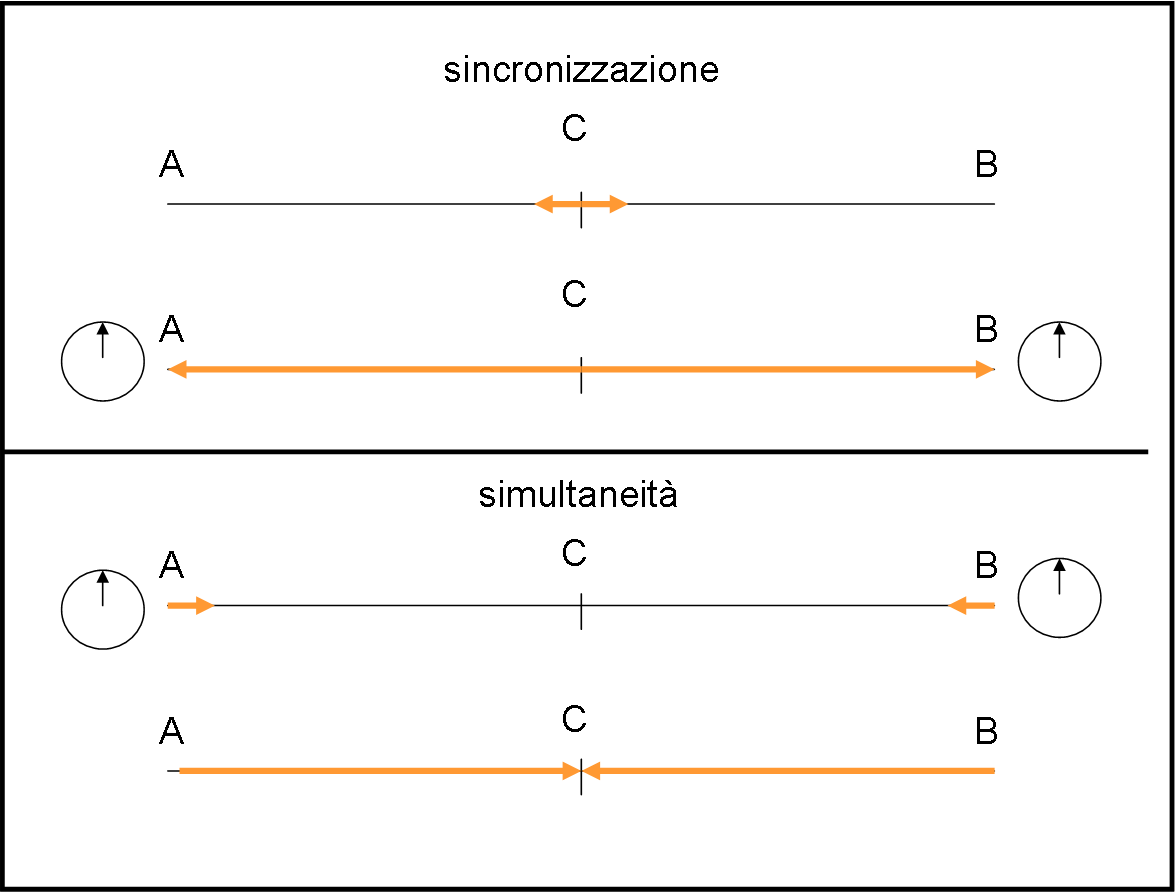
Affrontiamo nuovamente la simultaneità di due eventi e la sua relatività rispetto a due sistemi inerziali in moto relativo. Lo facciamo in modo ultra semplice e qualitativo, ma, passo dopo passo, arriviamo quasi automaticamente a rappresentare il concetto di base, quantitativamente, sul diagramma di Minkowski. Concludiamo con un piccolo “test” di verifica.
Questo articolo vuole solo essere una esercizio per mettere alla prova la comprensione dei concetti che abbiamo descritto finora. E’, quindi, un invito a passare all’azione e controllare se avete digerito la logica descritta finora. Completato l’esercizio, ci fermeremo a osservare i risultati ottenuti e cercheremo di capire la loro “stravaganza”. Questa riflessione servirà come punto di partenza per una trattazione molto più tecnica e generale.
Continuiamo a prendere conoscenza con il diagramma di Minkowski. Abbiamo visto che la trasformazione di Lorentz trasforma un sistema di assi ortogonali in un sistema di assi non ortogonali. Per definire il nuovo sistema è, però, necessario ricavare l’unità di misura sui nuovi assi ottenuti con la trasformazione.
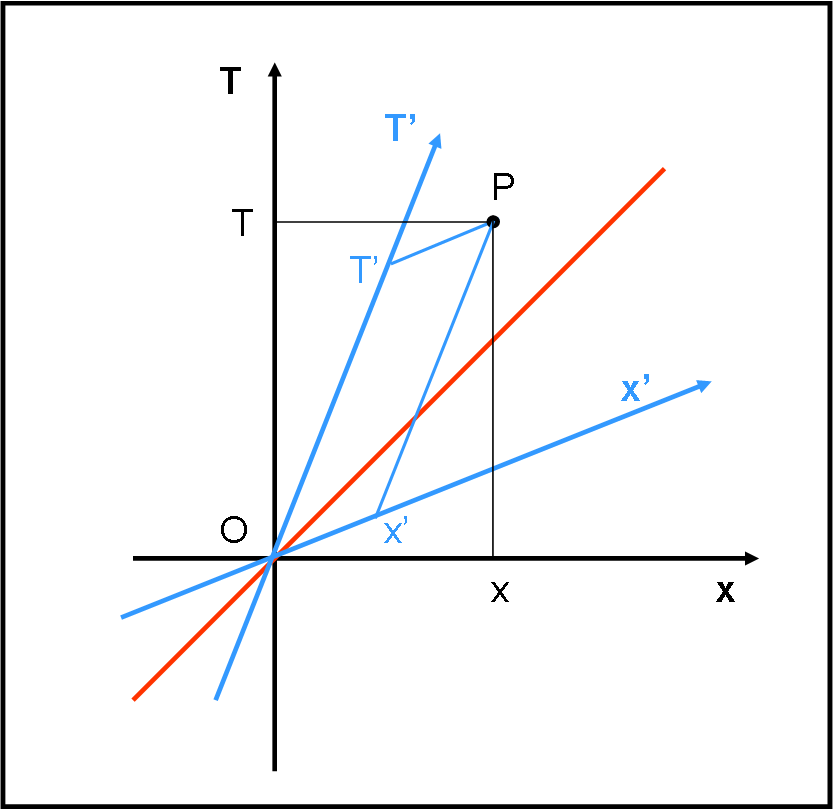
Rispondendo all’ultimo quiz sulla simultaneità, introduciamo ufficialmente il diagramma di Minkowski. Questa parte è estremamente semplice, ma il concetto deve essere compreso molto bene per non andare in crisi non appena introdurremo una nuova distanza invariante.
Innanzitutto, devo chiedere scusa a SuperMagoAlex, mio insostituibile amico-collega-assistente. Tra pochi giorni terrà una conferenza a un pubblico di astrofili e appassionati sul concetto di “tempo” o giù di lì. Un’impresa non facile che lo sta occupando a "tempo" (quasi) pieno. Mi ha chiesto personalmente di non inserire nuovi quiz che lo distrarrebbero… Però, però, Lorentz mi ha contattato, mi ha “bacchettato” e devo intervenire. Inserisco, quindi, un nuovo quiz analogo a quello precedente. Tuttavia, non darò la risposta fino a quando SMA non avrà avuto il tempo di dedicargli un po’ di tempo (più o meno una settimana). L’attesa avrà come premio la pubblicazione, sul sito del nostro “circolo”, dell’intera conferenza. Forza SMA siamo tutti con te! Gli altri, intanto, facciano un po’ di ripasso e qualche piccola operazione matematica. Come vedete, il quiz ha solo due asterischi e quindi è veramente facile…
La determinazione della linea di simultaneità è fondamentale per entrare nel mondo del diagramma di Minkowski. La determineremo anche matematicamente, ma prima è molto meglio ricavarla in modo grafico e immediato (o quasi…). Essa ci descrive l’asse x’ da accoppiare a t’, per un sistema in movimento, ed è la base per descrivere la dilatazione dei tempi e la contrazione delle lunghezze.
Il quiz che vi pongo DEVE essere risolto graficamente e solo attraverso la logica. Non è necessario (anzi NON voglio proprio) che siano utilizzate le formule che abbiamo imparato finora (capito Alvy...?). La motivazione del quiz è solo quella di capire se abbiamo digerito bene i concetti descritti finora e che ci hanno permesso di creare le basi fondamentali della relatività ristretta. Qualsiasi formula, che non sia una semplice proporzione, è del tutto inutile, dato che l’argomento sarà affrontato con ben altra attenzione nel seguito della nostra avventura nello spaziotempo di Minkowski.
In questo articolo di “passaggio” facciamo qualche riflessione sul vero significato di relatività e, in seguito, mostriamo come sia facile crearsi un sistema di riferimento a quattro dimensioni che abbiano la stessa unità di misura: il vero e proprio spaziotempo. Minkowski si avvicina sempre di più.
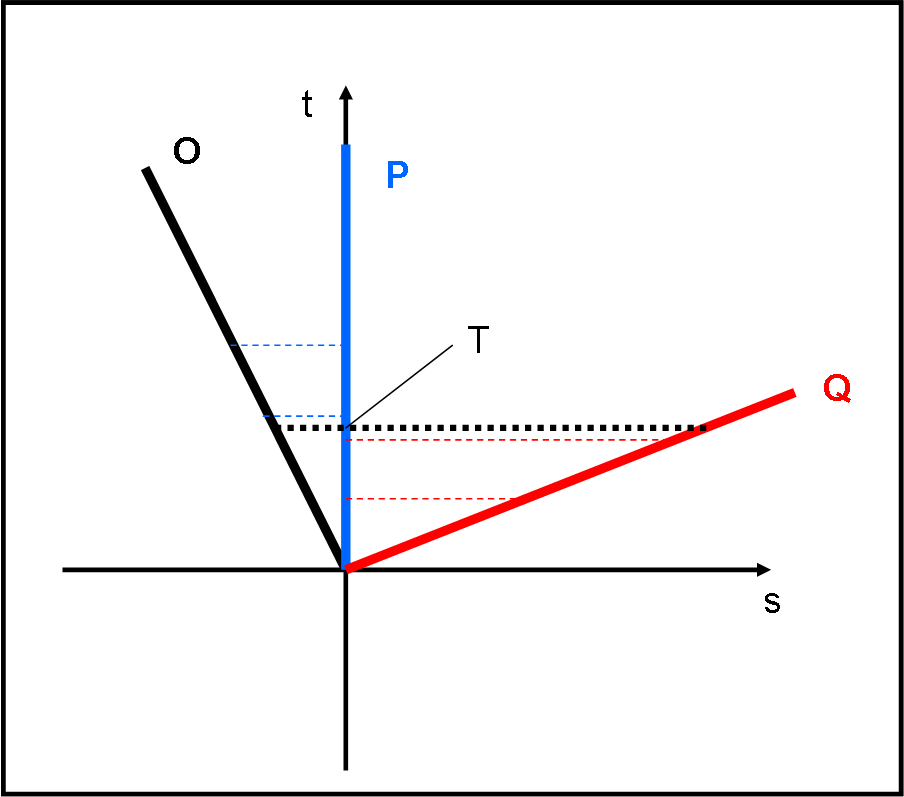
Lo, lo so, non picchiatemi. Avevo promesso di scrivere articoli brevi e invece ve ne propino uno piuttosto lungo. Tuttavia, ci sono almeno tre ragioni per non avere mantenuto la promessa. Innanzitutto, la prima parte riprende tale e quale quanto già scritto non molto tempo fa e quindi è né più né meno che un ripasso. La seconda è estremamente intuitiva e banale, soprattutto dopo aver seguito l’avventura di CE & Co. La terza, un po’ più “complicata”, non è divisibile: lo spazio-tempo galileiano deve essere mandato giù tutto assieme come una medicina… Non fatevi ingannare dall’apparente semplicità del diagramma. Deve diventare un amico fraterno e senza segreti se vogliamo proseguire verso quello di Minkowsky.
No, non illudetevi… non introduciamo ancora nessun argomento legato alla velocità della luce e alle trasformazioni di Lorentz. Bisogna prima preparare per bene il terreno. Innanzitutto, capire cos’è lo spazio-tempo, inteso come sistema di riferimento quadrimensionale in cui è possibile identificare perfettamente un evento. In altre parole, ciò che normalmente chiamiamo posizione di un punto nello spazio a tre dimensioni deve trasformarsi in evento nello spazio-tempo a quattro dimensioni. La matematica lo permetterebbe facilmente, ma noi preferiamo arrivarci con il ragionamento. Vedrete che non è “tempo” perso!
Non ce la caveremo con poche puntate… potete esserne certi. Sia perché voglio andare avanti con i piedi di piombo (un po’ come se il mio orologio rallentasse…), sia perché di materiale da esporre ce n’è veramente tanto. Alla fine metterò tutto assieme, ma sarebbe molto meglio seguire le singole puntate, in modo da evidenziare subito eventuali problemi interpretativi. Ricordatevi, però, che tutto ciò che dirò, cercando di esprimerlo con una semplice geometria, è basato solo e soltanto su un approccio squisitamente matematico. Insomma, non amare la matematica vuol dire non amare la Scienza…

