Il giro della morte: l'emozione più grande al Luna Park. Cerchiamo di capirlo bene attraverso un semplice problema.
Tre paradossi della fisica che sembrano "ridicolizzare" la forza di gravità e la forza centrifuga.
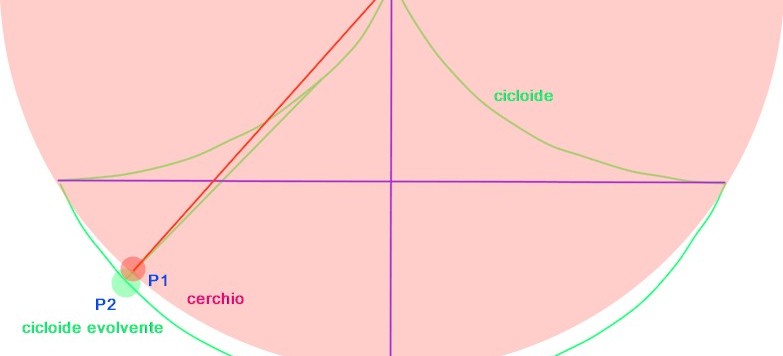
Tre secoli e mezzo fa, Christian Huygens pubblicava quello che può essere considerato il suo capolavoro: Horologium Oscillatorium, un'opera che assieme al Discorso sulle due nuove scienze di Galileo e ai Principa Mathematica di Newton, rientra fra i tre lavori scientifici più rilevanti del 17°secolo.
Nell'Horologium Oscillatorium si parla,tra molte altre cose, di orologi a pendolo e di cicloidi. Perché, Huygens, aveva capito che solo affidandosi al particolare profilo della cicloide si sarebbe riusciti ad ottenere una traiettoria migliore di quella circolare per il movimento del pendolo.
Vorrei sfidare chiunque, che sia giunto esattamente al Polo Nord, a dimostrare che la Terra non sia piatta. Soprattutto se può muoversi di solo pochi metri attorno all’asse polare (ultimamente lo hanno dipinto di rosso per ricordare che il clima terrestre è ormai veramente “bollente”). Toccando l’asse polare (non muovetelo troppo, mi raccomando…) si avverte, però che, anche se piatta, la Terra gira attorno a quell’asta che punta quasi perfettamente verso la stella polare (le farà mica il solletico?).
Fabricius usa la pietra Lagrangiana per risolvere i problemi. Con la parola magica KappaU li chiude nella pietra che colpita dalla luce Eulgrange emette la soluzione. Noi ci dobbiamo accontentare del metodo di Lagrange che attraverso l'energia cinetica (K) e l'energia potenziale (U) ci fa costruire la lagrangiana. La lagrangiana elaborata con l'equazione di Eulero-Lagrange ci fornisce la soluzione.
Nelle puntate precedenti abbiamo costruito alcuni esempi di lagrangiane di corpi liberi e vincolati ed abbiamo preso confidenza con le derivate che sono utilizzate nella equazione di Eulero-Lagrange.
In questa quinta parte dell'articolo finalmente arriviamo alla equazione di Eulero-Lagrange.
In questa terza parte proseguo a proporvi alcuni esempi di lagrangiane. Vedremo alcune lagrangiane di corpi vincolati a seguire delle traiettorie predefinite che mettono in evidenza alcune caratteristiche importanti della lagrangiana e del metodo di Lagrange. Proprio lo studio di questo tipo di problemi ha dato origine al metodo di Lagrange.