Per calcolare pi greco basta un dado un po' speciale. Ma un computer saprebbe sveltire e migliorare il risultato. Grazie alla sua "intelligenza"? No, solo alla sua stupidità che lo rende uno schiavo utilissimo e rapidissimo.
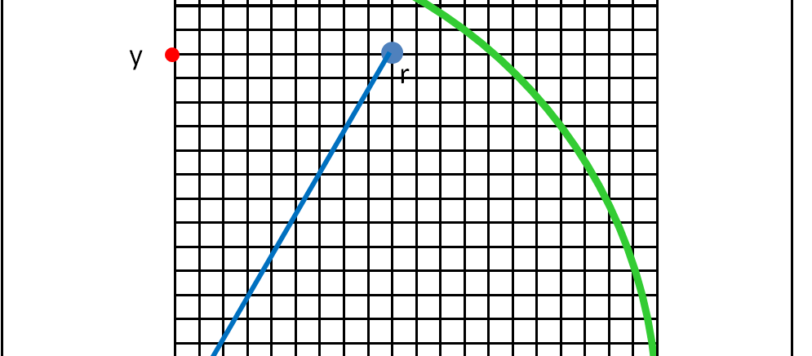

Per calcolare pi greco basta un dado un po' speciale. Ma un computer saprebbe sveltire e migliorare il risultato. Grazie alla sua "intelligenza"? No, solo alla sua stupidità che lo rende uno schiavo utilissimo e rapidissimo.
Abbandoniamo il quiz sulla quadratura del cerchio, ma colleghiamo il problema a un genio assoluto di arte e di scienza.

Nella soluzione che propongo a questo quiz ci si rifà pari pari alla formula trovata da Dirac, sia sostituendo pi greco al numero 2 sia scrivendo 2 in altro modo... Ringrazio ufficialmente Karl, Andy e Fabrizio per la volontà, l'interesse e le capacità dimostrate!
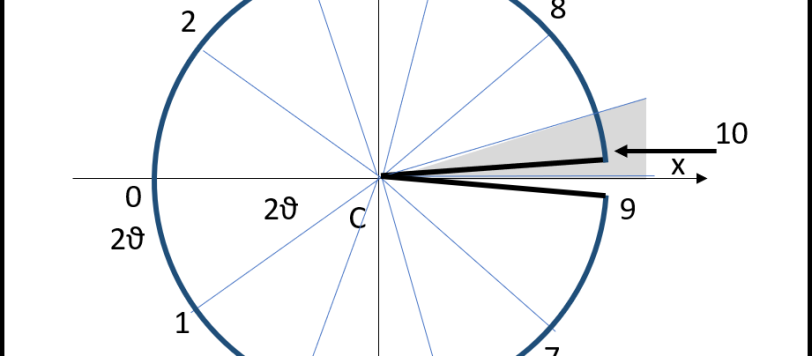
Abbiamo visto che gli urti tra due masse e di una di loro contro una parete riesce a regalarci le cifre significative del pi greco. Analizziamo a fondo il perché, anche se Francesco ha già dato una risposta esauriente. Ci troviamo di fronte a un problema puramente matematico espresso attraverso la meccanica e dimostrabile con la semplice geometria. Un gran bell'esempio di interdisciplinarità.
La prima parte, ossia quella relativa a cosa "saltava fuori" era decisamente facile, anche se molto noiosa...

In questo articolo descriviamo più accuratamente il metodo di esaustione e ci dedichiamo a seguire passo passo l’approssimazione del pi greco trovata da Archimede. Una trattazione a livello di scuola media, ma utilissima anche per chi voglia capire veramente come si può arrivare a conclusioni geniali senza algebra e senza trigonometria. Un’immersione completa nella mente del grande siracusano. Riportiamo anche la soluzione della quadratura del cerchio per mezzo della cicloide e un piccolo quiz.

Sicuramente, un apporto fondamentale alla determinazione del pi greco o, se vogliamo, alla quadratura del cerchio si deve ad Archimede. Particolare importanza e suggestione ha il suo metodo meccanico a cui avevamo già accennato nell’articolo sul calcolo della superficie e del volume della sfera. Iniziamo a eseguire la quadratura di una parabola…
Un’altra piccola sosta nella storia del pi greco per cercare di risolvere (inutilemente) il terzo grande problema della geometria antica: la duplicazione del cubo con riga e compasso. Le soluzioni non classiche hanno però una storia affascinante che vede protagonista, come “meccanico” addirittura Ertostene, l’uomo che misurò la circonferenza della Terra con una precisione fantastica.
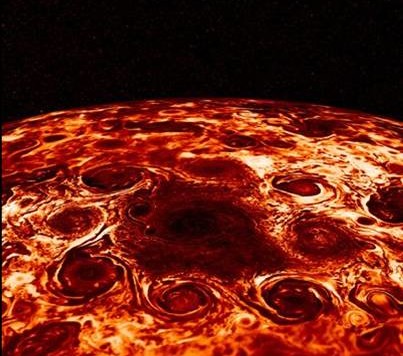
Il titolo è sicuramente astruso, ma la spiegazione è semplice. Ho tralasciato a lungo le impressionanti immagini che Juno ha inviato a terra, in attesa di potermi “inventare” qualcosa di speciale (ormai mi conoscete). Ora è giunta l’ora di unire scienza e fantasia, soprattutto dopo tutta la geometria che abbiamo ingoiato attraverso strade su monti conici e le stupefacenti ricerche sulla quadratura del cerchio (e non solo) degli antichi greci.

Torniamo al nostro pi greco che avevamo lasciato al tempo degli egizi. Esso non è ancora giudicato una vera costante, ma il valore di un certo rapporto tra lunghezze o aree. Ma se il pi greco è legato strettamente alla quadratura del cerchio, altri problemi appaiono insolubili per via puramente geometrica.

Non considerate noioso questo articolo. Da un lato abbiamo a che fare con problemi di geometria apparentemente più che banali, ma, dall'altra, entriamo prepotentemente nella Scuola di Atene, dove dire "geometria" è un modo di vivere e di pensare. Seguendo poche regole prefissate, siamo in grado di ottenere ciò che l'algebra e la geometria analitica ritroveranno dopo secoli. Un viaggio entusiasmante e -soprattutto- molto divertente.

Irrazionale (non è quoziente di due numeri interi), trascendente (non può essere radice di polinomi con coefficienti razionali), non è una costante fisica, ma puramente matematica; tuttavia, sembra che non si riesca descrivere l’Universo senza di essa: entra dappertutto, dal micro al macrocosmo. E’ solo una necessità dell’uomo, che è costretto a inserirla per tentare di spiegare le leggi della Natura, o è invece un qualcosa di profondamente radicato nell’essenza stessa del Cosmo? Forse non lo sapremo mai, ma il pi greco e la sua storia sono un punto chiave di tutta la Scienza e non potevamo fare a meno di dedicargli un articolo approfondito.

Vi sono state risposte molto accurate e non mi resta che riportare la soluzione nel modo più semplice e dettagliato possibile. In modo quasi imprevisto, è saltato fuori il solito, immancabile, π. Un dovuto omaggio proprio in concomitanza con il giorno dell’anno dedicato a lui. Forse, tra non molto, sarebbe il caso di dargli una visibilità ancora più ampia, a partire dalla storia antica.
Potevamo iniziare subito con il calcolo dell’area definita da una funzione qualsiasi (e non solo da una retta come fatto finora utilizzando spazio, velocità e accelerazione). Tuttavia, prima di far ciò, è più che doveroso richiamare i metodi che hanno portato Archimede a ricavare il valore di pi greco e dell’area del cerchio. Due problemi che hanno accompagnato l’uomo per tutta la sua storia e che hanno visto le “sommatorie” come attori fondamentali. Il lavoro di Archimede ha, in pratica, iniziato la storia degli integrali.