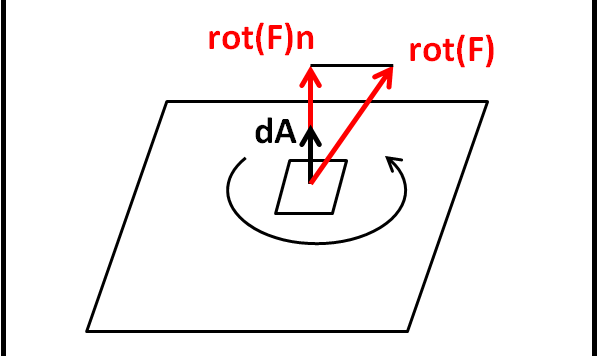
Descriviamo i due teoremi fondamentali (della divergenza e del rotore) che ci permetteranno di passare dalle equazioni di Maxwell in forma integrale a quelle in forma differenziale.
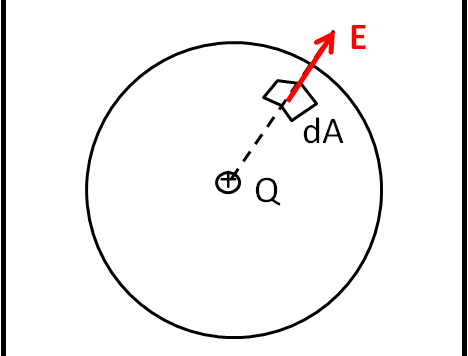
Cominciamo da capo, cercando di scrivere con un linguaggio matematico (semplice) le varie equazioni. Scusate le ripetizioni, ma è meglio battere il chiodo due volte e anche più. Come già detto non spaventatevi dei segni di integrazione o di derivata e pensateli come somme e differenze lungo una certa direzione.
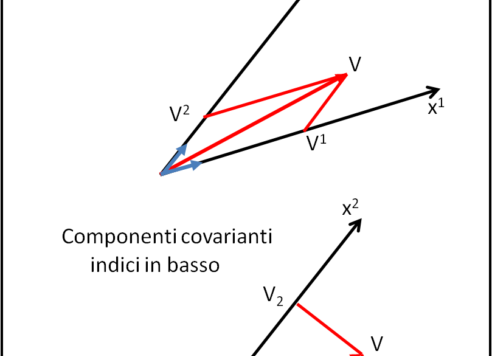
E' ora di trasformare i tensori e di introdurre, in modo estremamente didattico, le coordinate controvarianti e covarianti. Le cose si complicano un poco e devo limitarmi a dare alcune definizioni ...
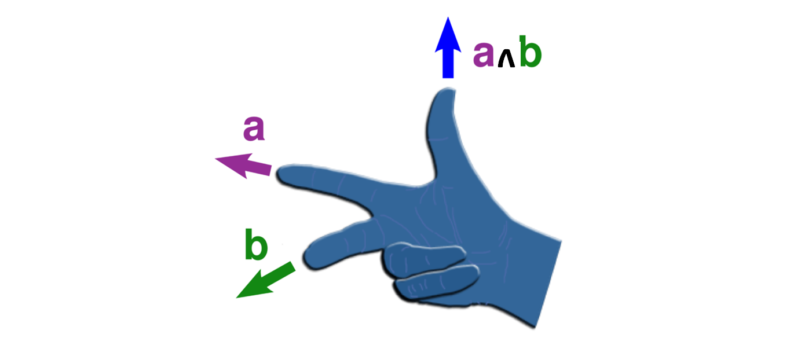
Introduciamo nuovamente i tensori, tenendo ben presente che abbiamo lavorato tanto per riuscire a manipolare correttamente le loro coordinate, cambiando sistema di riferimento. Ci aspetta un bel ... "lavoro"!
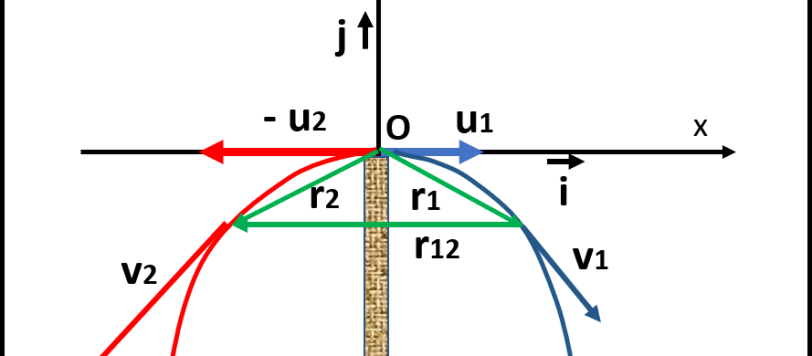
Un problema che si risolve molto elegantemente lavorando solo con i vettori (e i versori), ricordando una classica operazione tra di loro.
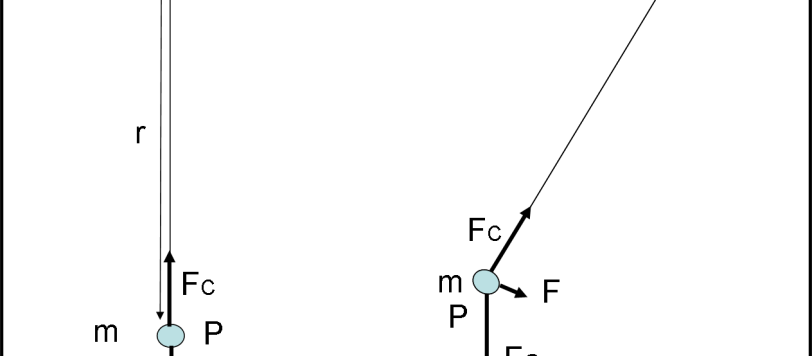
Il titolo sembra solo una constatazione e nulla più. Spesso viene presa come tale e da essa si innesca il discorso del Pendolo di Foucault e della rotazione della Terra. Tuttavia, esiste una dimostrazione molto pignola che fa uso dei prodotti scalari e vettoriali. Farà un gran piacere agli amanti dei vettori e delle operazioni collegate.
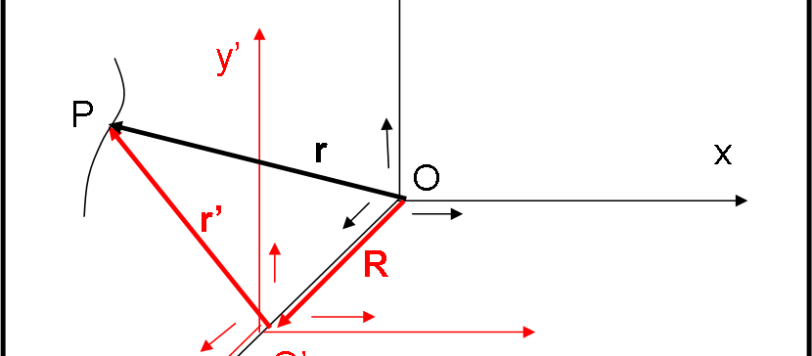
Beh... Coriolis non ha aspettato tanto (oggi ho deciso di lavorare solo di testa e non di braccia...). Per cui, ecco la nuova versione della prima parte della trattazione della forza di Coriolis, estesa e sicuramente più completa. Fa sicuramente uso di un po' di matematica semplice e recupera nozioni sui versori, vettori, prodotti scalari e vettoriali. Una bella rinfrescata non farà male... Il risultato, però, è estremamente utile per capire al meglio la "nascita" delle forze fittizie in generale. Lo scopo va, quindi, ben oltre la forza di Coriolis.
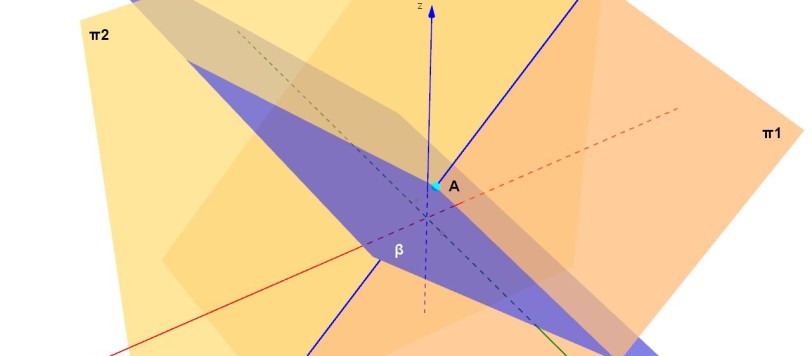
Nel precedente articolo, che potete rileggere QUI, ho introdotto il concetto di parametri direttori di una retta nel piano. In questo estendiamo il concetto alla retta nello spazio e al piano. Passiamo, quindi, nel riferimento cartesiano dello spazio.
Sappiamo già che la parallasse stellare era stata prevista da quel genio assoluto che era Aristarco, che aveva anche cercato inutilmente di misurarla. Sarebbe stata la prova diretta della teoria eliocentrica. Purtroppo per avere questa “prova” si dovette aspettare il 1727 d.C. per merito dell’inglese James Bradley, ma attraverso un fenomeno del tutto inatteso. Lasciatemi colorire un po’ la “storia”.
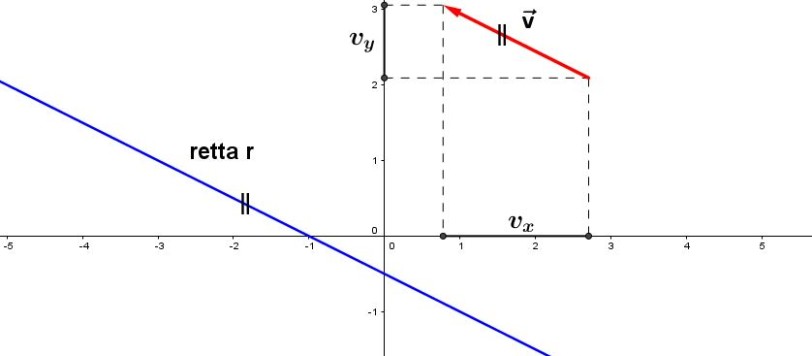
In questo articolo e in quello successivo intendo illustrare un elemento sinora da me mai citato ma che , come vedremo, si rivela molto utile nella trattazione di problemi di geometria, in particolare quella dello spazio. Tale elemento caratterizza una retta, indicandone la direzione, oppure un piano, consentendoci di individuarne subito tutte le infinite rette ad esso perpendicolari. Scopriremo che sia la retta sia il piano si "portano dietro" questo elemento come una targa identificativa, che a noi basta quasi leggere per conoscere subito, in termini analitici, la direzione della retta o la giacitura del piano.
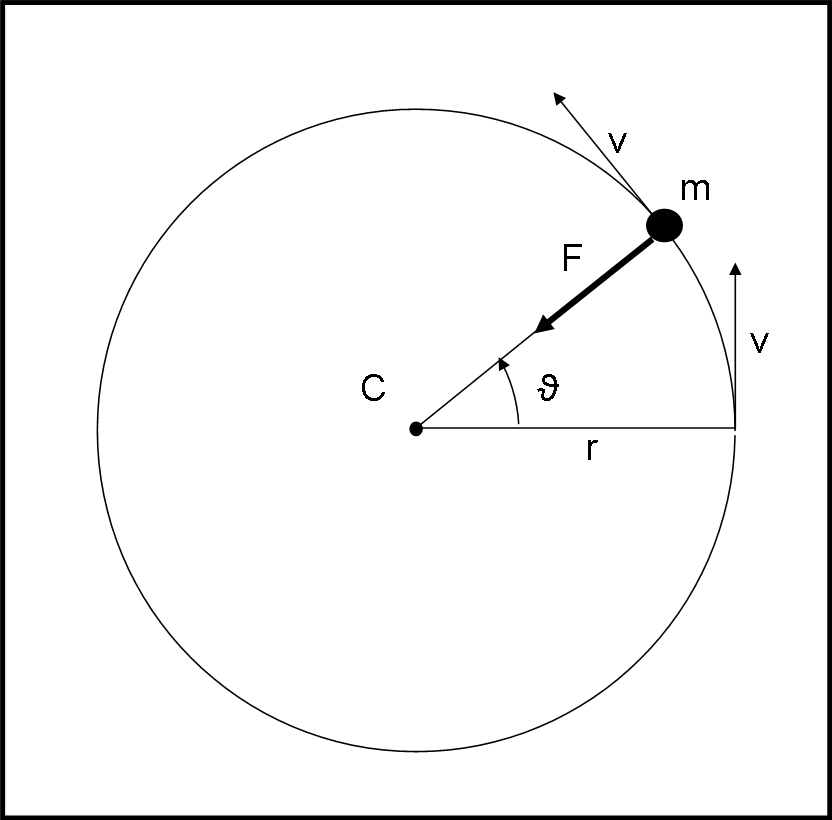
Per definire e descrivere il momento angolare e le sue proprietà è bene partire fin dall'inizio. Ed ecco che prima di arrivare a lui facciamo la conoscenza dei vettori, delle loro operazioni, della quantità di moto e dei principi della dinamica: una specie di riassunto di gran parte della dinamica classica. Senza dimenticare, ovviamente, la conservazione della quantità di moto e del suo figliolo momento angolare. Per far ciò useremo qualche colpo di scherma, un po' di Divina Commedia, qualche vite e/o qualche mano destra. Infine, mediante l'applicazione del momento angolare a un sistema particolare, introdurremo la dinamica dei moti circolari che imitano quasi perfettamente quelli traslatori o lineari.
Questo quiz non merita spiegazioni supplementari, dato che si risolve attraverso le regole descritte nei primi due capitoli dedicati al momento angolare, in cui si introducono i vettori, le loro operazioni e l’uso dei versori.
Rimaniamo sempre tra i vettori, ma iniziamo a studiare il loro prodotto. Dato che i vettori sono grandezze veramente speciali non si accontentano di un solo prodotto, ma ne pretendono due. Cominciamo con quello “scalare”. Ci faremo aiutare dal grande Cyrano de Bergerac: “ed al fin della licenza io tocco!”