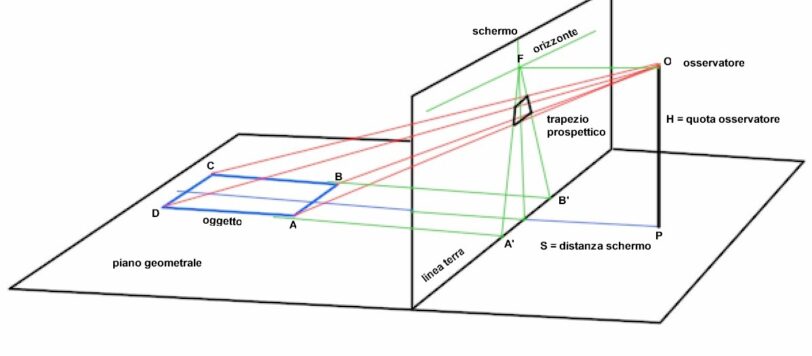
Nel precedente articolo intitolato “il pavone planò e cosa vide?” avevo promesso che avrei ripreso l'argomento utilizzando un quadro prospettico in posizione mobile (a distanza costante dall'osservatore). Questo accorgimento permette di risolvere il problema di rappresentare in prospettiva centrale la visione durante la planata in base a semplici relazioni che legano le variabili.
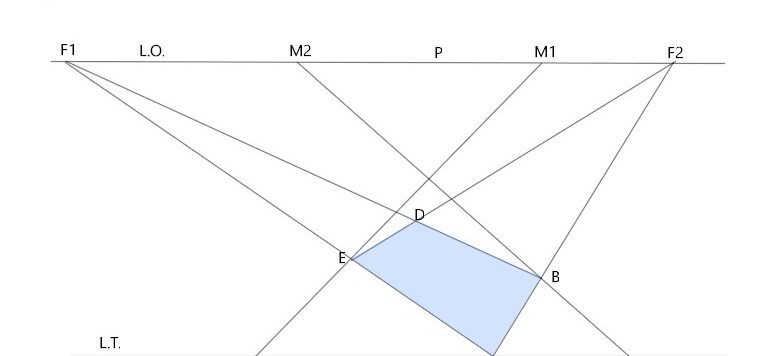
Il metodo cosiddetto “dei Punti Misuratori” è un modo molto efficace di disegnare le prospettive accidentali utilizzando direttamente le misure reali degli oggetti da rappresentare.
Il pavone vola, non come un'aquila ma abbastanza da vedere le cose dall'alto e quando plana, come tutti quelli che planano, vede il terreno avvicinarsi e le linee di fuga prospettiche mutare la loro inclinazione. Che mai vedrà in quei pochi istanti prima dell'atterraggio?
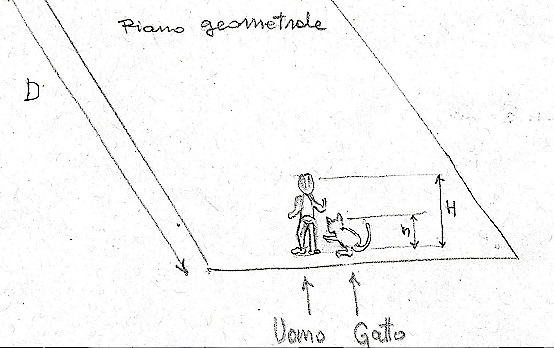
Prendendo spunto dal racconto "I miei umani" pubblicato recentemente da Gatto Nelson e da una serie di articoli di Enzo sulle tecniche della prospettiva mi è venuta la balzana idea di produrre una animazione che mostrasse cosa vedono un gatto ed il suo socio umano mentre, insieme, si muovono alla medesima velocità, osservando sul pavimento il disegno di un quadrato.
Riprendiamo un argomento che forse è stato trattato in un periodo in cui, giustamente, i nostri lettori potevano finalmente godersi un po' di vacanze.
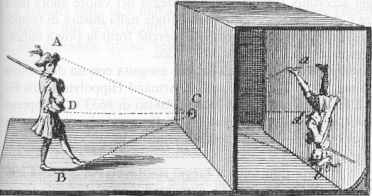
Abbiamo imparato in modo molto schematico, ma sufficiente allo scopo, a disegnare ciò che il nostro occhio vede. Esso vede tutto proiettato su un piano e in tale piano tutte le linee parallele devono convergere in un punto. In altre parole, abbiamo introdotto la prospettiva centrale, ossia quella forse più ovvia e comune. Attraverso di lei è possibile finalmente creato uno spazio reale in cui inserire, come volumi ben definiti, anche le figure siano esse oggetti, edifici o anche persone. Il Rinascimento insegna...
Continuiamo con la prospettiva centrale, muovendo un poco il nostro rettangolo.
E' tanto che avrei voluto parlare di prospettiva e di altre due tecniche di descrizione di ciò che realmente vede l'occhio e della sua rappresentazione su un piano. Questo è un nostro limite... dato che ciò che vediamo viene sempre proiettato su un piano. Il problema quindi si riduce a una rappresentazione bidimensionale della realtà tridimensionale in cui viviamo. Se aggiungiamo la mia passione per l'arte si comprende questa esigenza. Sarà, però, un approccio del tutto personale che, quindi, potrebbe anche essere perfezionato nel tempo, magari quando vi sarà un ritorno dalle ferie di moltissimi lettori. Insomma, partirò per "istinto" e poi, grazie anche ai vostri commenti, cercherò di essere più rigoroso.
Non possiamo dire più di tanto per non rovinarvi la sorpresa, ma è con grande piacere (e un pizzico di emozione) che riproponiamo questo racconto per offrirvelo come aperitivo in attesa di un gustoso banchetto che il prof. sta cucinando.
Chi ci segue da tempo si ricorderà di Astericcio & co. che affrontano temi intriganti e lo fanno nel modo più semplice possibile: il tema di questo racconto è quella ideale staffetta tra due Giganti che ha dato impulso ad una delle più vivaci stagioni dell'intelletto umano, nella quale l'arte raggiunse vette forse mai più eguagliate. Se all'inizio potrà sembrarvi una favola per bambini, andate avanti e capirete presto che i bambini a cui si rivolge sono quelli di tutte le età.
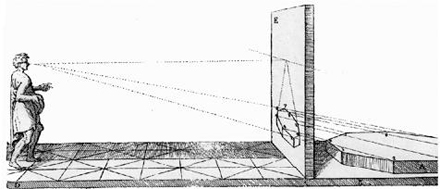
Riportiamo la soluzione, già largamente compresa da alcuni lettori, e spieghiamo perché solo uno dei tre amici è riuscito a risolverlo. Non poteva che essere Pappo, dato che tutto si collega al suo teorema… Il quiz è solo un inizio che ci porterà verso la geometria proiettiva e la sua fondamentale importanza nella storia dell’arte.
Anche se con un po’ d’indifferenza, andiamo, comunque, avanti con le deformazioni subite da un oggetto che si muove con velocità relativistiche. Il primitivo righello si sta trasformando in qualcosa di più concreto e si prepara a regalarci effetti del tutto imprevisti.
Non prendiamocela troppo con il nostro righello… lui, in fondo, ce la mette tutta per creare qualche gioco di prestigio divertente, in collaborazione con la lentezza atavica dei fotoni. Teniamo anche conto che ciò che troveremo alla fine era perfino “scappato” ad Einstein. Questa volta facciamo solo un passetto in avanti per poi lanciarci nella vera stregoneria.
Questo articolo è adatto a tutti, in particolar modo ai bambini che sprizzano fantasia da tutti i pori. Partiamo da una farfalla e ci accorgiamo che la geometria ci porta quasi automaticamente a spiegare alcuni tra gli oggetti più misteriosi e affascinanti del Cosmo. L'articolo era già apparso molto tempo fa, ma ho giudicato interessante riproporlo dato che con oltre 1800 articoli, i nuovi arrivati (e sono tanti) potrebbero trovare difficoltà a trovarlo nell'archivio... Se la cosa piacerà, ogni tanto faremo lo stesso con altri articoli particolarmente stimolanti e sempre attuali.