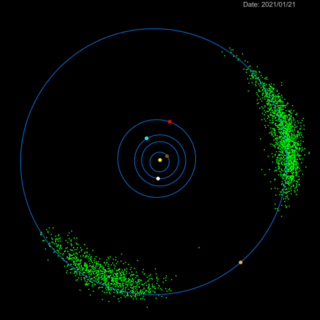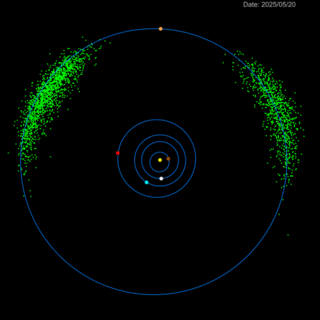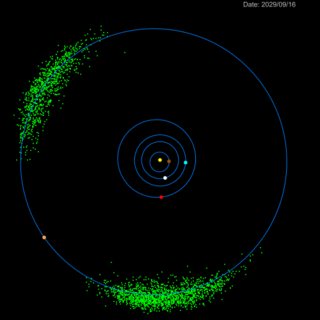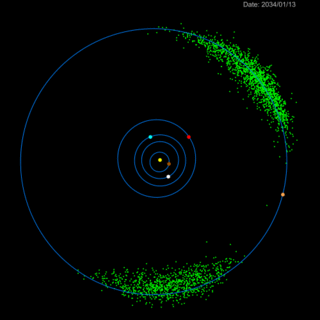
Anche se ben pochi l'hanno ricordata, la missione Lucy della NASA è partita pochi giorni fa per il suo viaggio che durerà 12 anni e che la porterà a visitare un certo numero di asteroidi troiani.
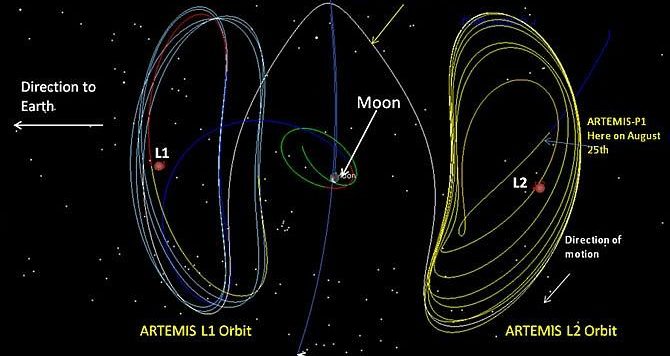
Concludiamo (per adesso, almeno) la nostra visita alle curve di Lissajous, analizzando in modo molto semplificato la loro applicazione naturale e artificiale, nel campo "terribile" della Meccanica Celeste.
Descriviamo a cosa va incontro il nostro Giacomino. Su consiglio dell'inesauribile Maurizio abbiamo anche valutato l'ipotesi di una scala costruita e fissata sulla Luna. Ovviamente, abbiamo avuto bisogno dell'aiuto dei Papallicoli... In questo modo, abbiamo perfettamente simulato le due piante di fagiolo del racconto originario...
Il problema dei tre corpi è ancora impossibile da risolvere per via analitica. Tuttavia, ammettendo che una massa sia trascurabile rispetto alle altre due, o imponendo condizioni particolari, esso può essere risolto come ci ha insegnato il grande Lagrange (De La Grangia, in realtà). Un argomento di interesse fondamentale sia per la Meccanica Celeste (sappiamo quanto siano importanti i punti lagrangiani per i i telescopi spaziali) che per l'evoluzione stellare dei sistemi doppi stretti (Lobi di Roche). In questo articolo cerchiamo di trattare la problematica nel modo più completo possibile. Esso si può trovare anche negli Approfondimenti.
Inseriamo, per ultimo, l’articolo relativo ai punti lagrangiani che, forse, da un punto di vista puramente fisico, doveva essere il primo. Poco male, dato che accorperemo i quattro articoli in uno solo negli Approfondimenti. Ciò che diremo è in parte già stato affrontato in varie occasioni e in particolare nell’articolo dove si era definito il campo gravitazionale di una singola massa, la famosa ragnatela. Aggiungiamo anche, per i meno preparati, qualche discorso sull’energia meccanica. Poi finalmente ci dedichiamo alla doppia ragnatela … energetica.
Questo articolo è un piccolo capolavoro di logica ed eleganza (non certo per merito mio…). Vi invito a leggerlo senza paura. Esso presenta la determinazione dei punti lagrangiani L4 e L5, nel modo più generale possibile, seguendo la strategia illustrata nel 1999 da I. Vorobyov dell’Università di Vienna. Un metodo di una semplicità disarmante, che io ho solo cercato di arrangiare in modo veramente elementare (matematica e geometria delle scuole medie).
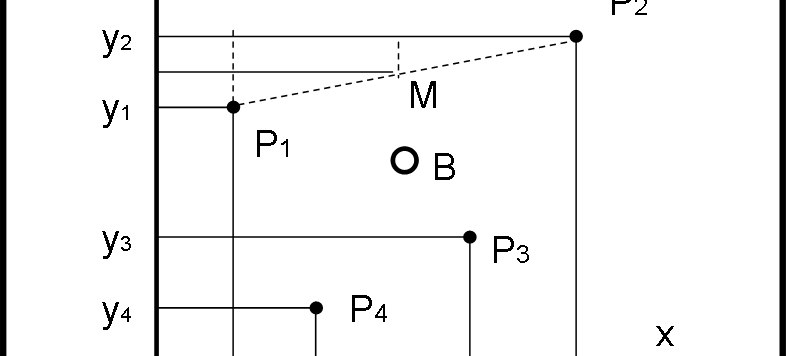
Abbiamo spesso pensato al campo gravitazionale, generato da una grande massa, come a una enorme ragnatela, capace di catturare e gestire il moto di un piccolo corpo che gli si avvicini troppo. In parole povere, siamo parlando del problema dei due corpi, discusso non molto tempo fa. E’ ora di passare a una doppia ragnatela e vedere cosa è capace di fare. Parleremo di baricentro, di punti lagrangiani, di lobi di Roche e tante altre belle cose che in parte già sappiamo, ma che è bene riassumere e trattare con maggiori dettagli.
Il vantaggio di potersi sistemare in punto lagrangiano… Proprio adesso che avevo intenzione di continuare la trattazione completa dei punti lagrangiani (come promesso), ecco che una sonda della NASA ci manda un video eccezionale di un’eclissi della Terra da parte della Luna… Immagini sempre emozionanti…
In questi giorni si parla (abbastanza) di un pianeta che appartiene a un sistema triplo. I titoli si lanciano su situazioni da film di fantascienza e si pensa soltanto alla visione di tre albe e di tre tramonti e/o di un pianeta riscaldato da tre soli (non riporto le fonti, ma sono facili da recuperate). In realtà la situazione non è poi così strana e rappresenta un bellissimo problema dei tre corpi (e magari, in futuro anche dei quattro). Affrontiamolo, brevemente, sotto questo aspetto, ben più intrigante.
Come ho già detto, avrei intenzione di cercare di introdurre al meglio queste “grandezze” fisiche, che sembrano essere più o meno la stessa cosa, ma che differiscono soprattutto per l’approccio con cui sono state introdotte e definite. Parliamoci chiaro: nessuna è ottenibile facilmente e nella maggior parte dei casi se ne dà solo una visione approssimata.