Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica. Sfruttando i salti di un canguro papalliano (i canguri di Papalla sono perfettamente rotondi, ovviamente, e rimbalzano facilmente) affrontiamo il problema dell'urto anelastico, dopo che l'effetto Compton ci ha permesso di studiare gli urti elastici. Un vecchio quiz, ci permette […]
Questo lungo articolo mette insieme tutti quelli apparsi sulla Dinamica Relativistica. In particolare, mostra come si arriva "facilmente" alla più celebre formula dalle Fisica e ci dà un'idea di quanto la Relatività Ristretta sia necessaria alla Meccanica Quantistica. Chiudiamo un altro pezzo fondamentale della fisica moderna, prima di affrontare la Relatività Generale. Dopo un po' di permanenza negli articoli in evidenza, si sposterà negli "approfondimenti".
Abbiamo parlato spesso di urti completamente elastici e anche un po’ di quelli completamente anelastici (nella dinamica relativistica). Vale la pena, però, descrivere gli urti in modo più generale, partendo dagli urti anelastici, proprio il caso che ci serve per il quiz sul papallo-canguro.
Permettiamoci ancora un piccolo “scherzo”, richiamando la particella più strana e più simpatica dell’Universo: il fotone. Questo articolo conclude la dinamica relativistica, che, al più presto, metteremo tutta assieme negli approfondimenti.
La fantascientifica idea (ma non poi tanto) che vede in qualche modo coinvolto Hawking (soprattutto per rendere l’operazione fortemente mediatica) ci potrà permettere di mandare moltissime sonde su Alpha Centauri in un tempo non superiore a circa 20 anni. E magari, anche meno… La missione sfrutta un’amica di cui abbiamo parlato spesso ultimamente: la quantità di moto (e la sua conservazione).
Potevamo fermarci con l’articolo precedente. Tuttavia, non è male introdurre un QUIZ molto istruttivo. Anche senza tentare di risolverlo, è utilissimo seguirlo passo dopo passo. La soluzione alla prossima puntata.
Fatemi arrivare al dunque in modo molto personale e “quasi” allegro e spontaneo. Abbiamo incontrato lungo il percorso nuove grandezze che dipendono dalla velocità. Grandezze che cambiano, cambiando sistema di riferimento. Ciò che viene conservato sono le loro leggi di … conservazione. D’altra parte siamo o non siamo nella relatività ristretta? Tuttavia, pensandoci bene, qualcosa che non cambia c’è e questo fatto implica un nuovo invariante che lega l’energia con la mia grandezza preferita.
Siamo partiti con un urto elastico e poi abbiamo anche visto cosa capita in un urto anelastico, dove le masse a riposo, con una certa sorpresa, non si sono conservate nell’urto. La faccenda, però, è ormai abbastanza chiara: se non si conserva la massa ci pensa l’energia a mettere tutto a posto, dato che sono praticamente la stessa cosa. Questo esercizio riveste un’importanza veramente fondamentale per comprendere al meglio la rivoluzione einsteniana.
Dimostrato che nella relatività ristretta è necessario modificare la definizione della quantità di moto, affinché essa si conservi, imponendo che la massa del corpo in oggetto aumenti con la sua velocità, risulta chiaro che le leggi di Newton devono subire anch’esse delle modifiche strutturali, quando le velocità diventano paragonabili a quelle della luce. Cominciamo ad avvicinarci all'energia...
Chi vuole divertirsi ancora un po’ (è del tutto facoltativo) può arrivare alla stessa conclusione, utilizzando il ragionamento fatto da Feynman. E’ sicuramente un metodo più rapido, senza formule noiose, ma comporta un ragionamento finale sul risultato che potrebbe causare una qualche confusione nei meno attenti e concentrati. Sicuramente, è geniale come tutto ciò che ha fatto lui…
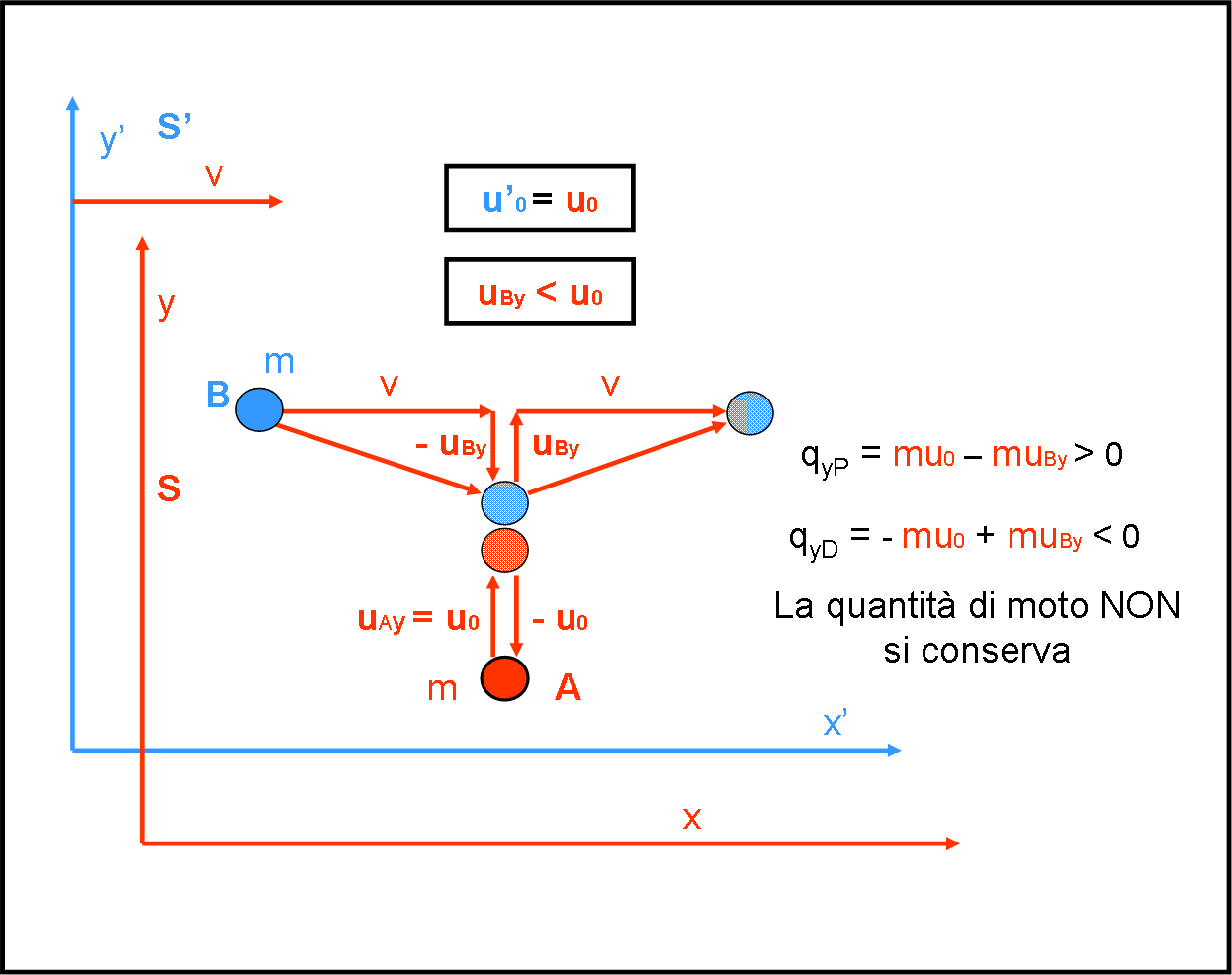
Questo articolo è molto corto. Preferiamo mangiare la “torta” a piccoli tranci per permetterci di gustarla fino in fondo. Dimostrare che la quantità di moto “classica” non si conserva nella Relatività Ristretta è un punto di arrivo fondamentale e va compreso perfettamente bene. Una conclusione, in realtà, banale, ma che ci obbliga a modificare tutta la dinamica conosciuta fino ad allora. Ricordiamo, comunque, che stiamo parlando di velocità comparabili a quella della luce. Se giocassimo a palline con un nostro amico che va in bicicletta niente cambierebbe rispetto alle descrizioni di Galileo.
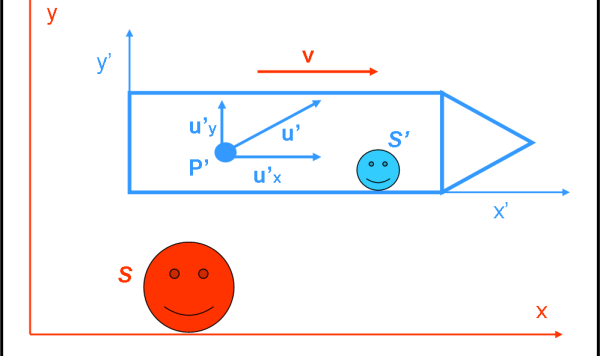
In questo secondo articolo costruiamo un esperimento relativo all'urto elastico di due palline, appartenenti a due sistemi diversi. Prima manteniamo fermi i due sistemi e dopo facciamo muovere il primo, rimanendo in ambito galileiano. Cosa succede alla quantità di moto delle due palline?
Avete pienamente ragione! Sono veramente inaffidabile: dico una cosa e ne faccio subito un’altra. Volevo aspettare a parlare di massa ed energia e seguire una trattazione accurata e tranquilla ed ecco che anticipo i tempi e derivo velocemente la più celebre formula della fisica. In realtà, questo articolo vive in modo del tutto indipendente dalla dinamica relativistica spiegata per gradi e con continuità. Possiamo digerirlo facilmente e poi proseguire per la strada maestra. Sapete, la mia inaffidabilità nasce dal bisogno interiore che ho di rendere tutti partecipi del maggior numero di concetti possibili. So che non avete tempo a seguire tutto, ma cominciamo a mettere nero su bianco, in modo che certi articoli non passino nel dimenticatoio e non vengano mai pubblicati. Spero che capiate la fretta di un vecchietto di 70 anni (passati)…
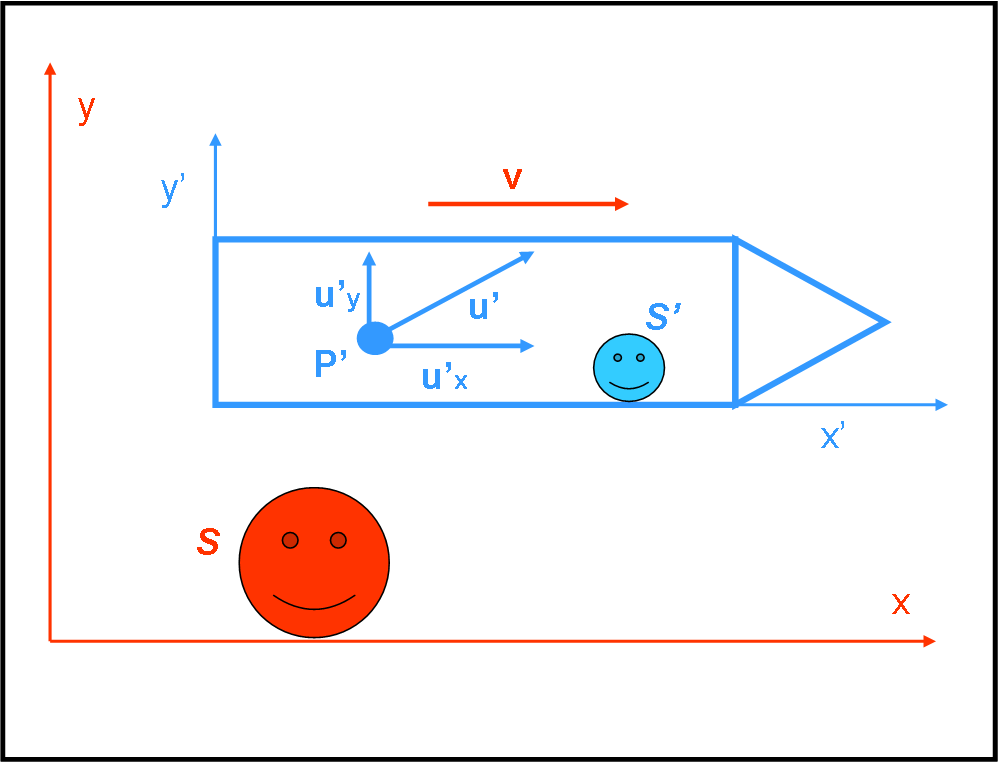
Siamo pronti per partire con la dinamica relativistica. Per far ciò è fondamentale descrivere, prima di tutto, come la quantità di moto sia costretta a cambiare per potersi conservare. Normalmente questa parte si dà per assodata o si spiega -spesso- in modo poco chiaro, incentrando tutto sulla massa relativistica, gioia e dolore dal punto di vista concettuale. Ho cercato di raggiungere lo scopo nel modo più semplice possibile, evitando, però, semplificazioni che avrebbero generato eventuali confusioni. Ho deciso di pubblicare questa parte iniziale della dinamica relativistica (DR) prima della fine degli integrali, in quanto non ne ha bisogno. Vi prego sinceramente di esporre tutti i dubbi senza paura. Ricordiamoci che senza questa base di partenza i nodi verrebbero, comunque, al pettine più tardi… Fatemi anche capire (in tanti) se … avete capito! Basta un OK...
A qualcuno potrebbe sembrare che io stia sollevando un sacco di problematiche concettuali e di ostacoli, nel tentativo di descrivere correttamente la quantità di moto relativistica. In giro per la rete si trovano determinazioni velocissime e che -a prima vista- sembrano del tutto logiche… sicuramente più rapide e semplici del procedimento che ho iniziato a descrivere con molta precauzione. Attenzione, però...
Per definire e descrivere il momento angolare e le sue proprietà è bene partire fin dall'inizio. Ed ecco che prima di arrivare a lui facciamo la conoscenza dei vettori, delle loro operazioni, della quantità di moto e dei principi della dinamica: una specie di riassunto di gran parte della dinamica classica. Senza dimenticare, ovviamente, la conservazione della quantità di moto e del suo figliolo momento angolare. Per far ciò useremo qualche colpo di scherma, un po' di Divina Commedia, qualche vite e/o qualche mano destra. Infine, mediante l'applicazione del momento angolare a un sistema particolare, introdurremo la dinamica dei moti circolari che imitano quasi perfettamente quelli traslatori o lineari.