Ancora un quiz molto semplice, che, però, fa riflettere.

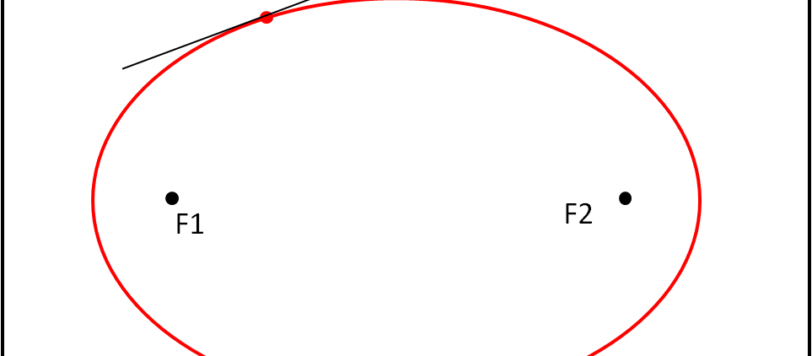
Prima di giocare con un biliardo un po' speciale, fatemi fare una domanda-quiz sicuramente non difficile.
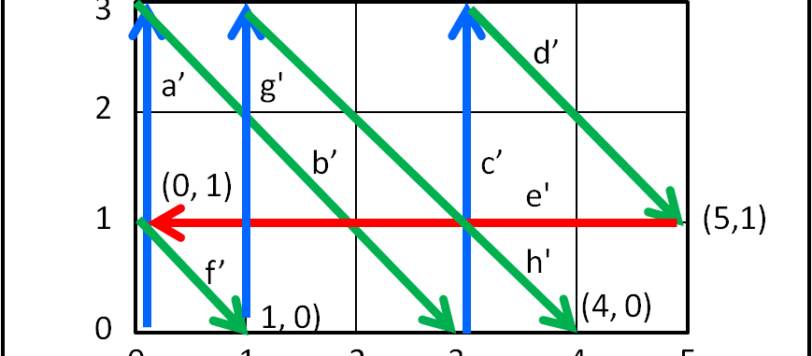
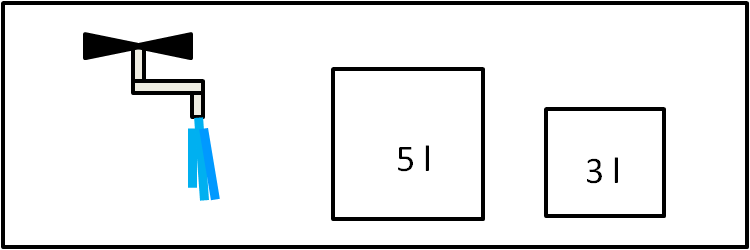
Il facile quiz sulle taniche da 5 e 3 litri è stato risolto brillantemente da Papalscherzone, ma mi ha fatto venire in mente un modo diverso per arrivare alla conclusione. Tra non molto ci divertiremo con i vettori e allora perché non usarli anche in questo caso?
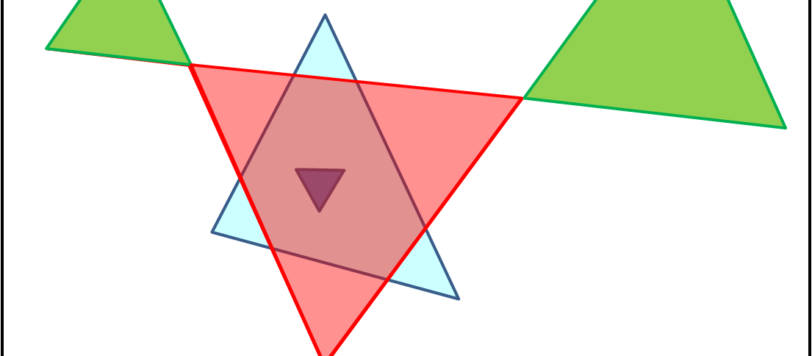
Avendo inserito una richiesta di dimostrazione che terrà terrà occupati a lungo i più "bravi", mi sembra giusto accontentare anche i meno esperti... In poche parole, non rispondano i soliti bravissimi solutori di quiz.
Non spaventatevi per i cinque asterischi! Il teorema che andiamo ad enunciare è di estrema semplicità (due soli asterischi) e può essere considerato veramente una magia "sfuggita" agli antichi greci. I cinque asterischi si riferiscono alla parte "nascosta", ossia alla dimostrazione, impresa tutt'altro che facile.
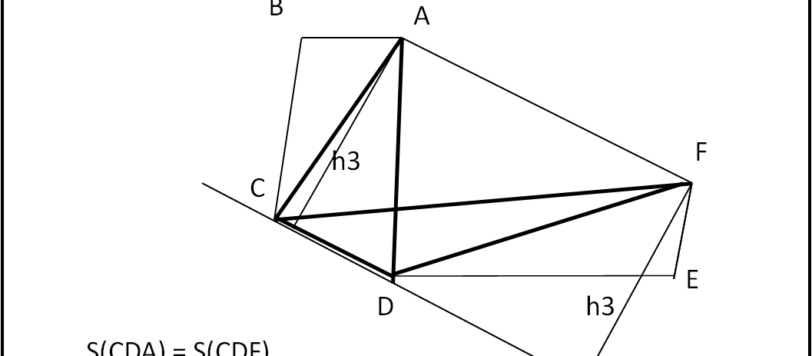
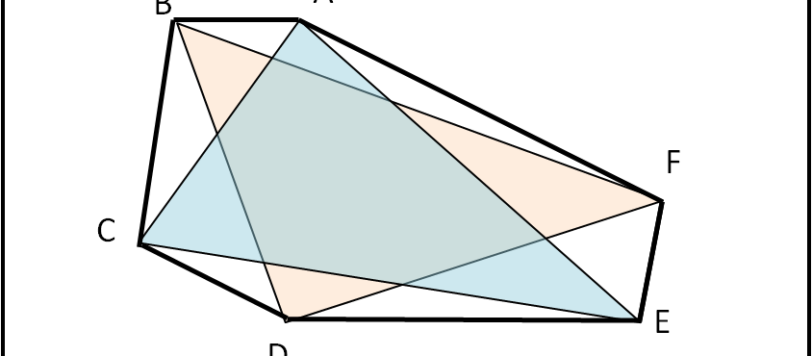
Com'era facile intuire, la soluzione al quiz sull'esagono diventa quasi immediata ricordando le aree dotate di segno. Comunque un grazie ad Artù e Fabry per le loro soluzioni alternative!
In realtà questo quiz meriterebbe meno di tre asterischi, ma bisogna avere l'intuizione giusta e ricordare qualcosa che abbiamo imparato da poco.

Un problema piuttosto semplice in attesa di qualcosa di veramente difficile, che rappresenta l'essenza stessa del ragionamento matematico e che ci farà scoprire un vero... miracolo, che interesserà tutti e non solo i più esperti. Un po' di relax prima di una prova ben più ardua .
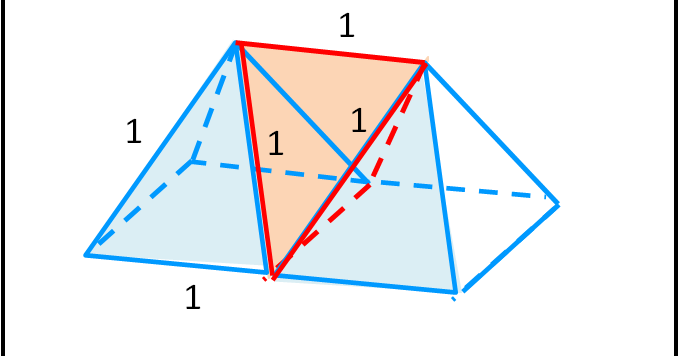
Quest'articolo tenta una dimostrazione geometrica unitaria della complanarità e non complanarità delle facce di solidi semplice come il tetraedro e la piramide. Lo fa attraverso le proiezioni e devo dire che la visione delle varie figure non è proprio banale, da cui i tre asterischi.
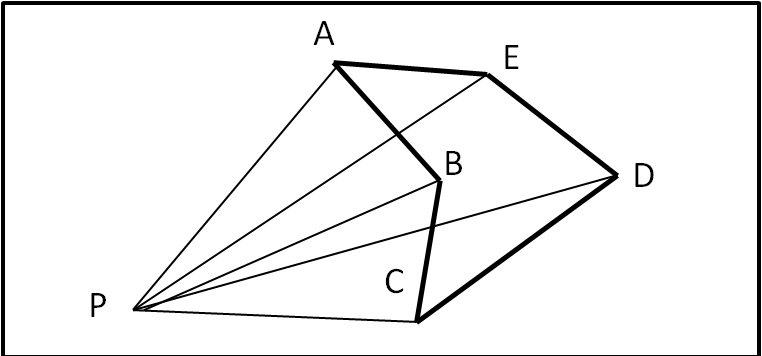
Innanzitutto, un bravo particolare a Leandro che in qualche modo (magari non il più semplice) è riuscito ad allacciare la scarpa... D'altra parte nel poco conosciuto metodo per il calcolo dell'area di un triangolo (e di un poligono qualsiasi) c'è la mano di Gauss. In realtà il metodo "laccio da scarpa" prende anche il nome […]

Un quiz abbastanza semplice per tenervi occupati mentre preparo la risposta al problema del "laccio da scarpa"
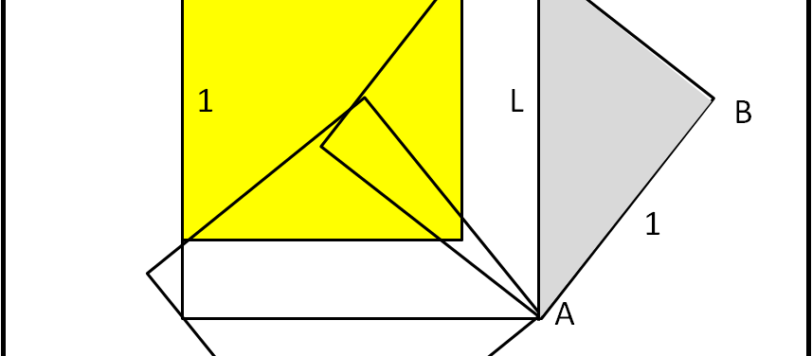
Un quiz che ha ottenuto poco successo, ma che ha visto la risposta qualitativamente esatta di Daniela. Direi che vale la pena, comunque, di darne anche il risultato quantitativo.

Un bel problema di geometria che abbisogna di un certo intuito e molto ragionamento. Affrontiamolo senza chiedere aiuto allo studio di funzioni, ma solo a un'analisi attenta di quello che abbiamo e di ciò che vogliamo trovare.

Come previsto, noi non siamo certo milioni, ma malgrado le ferie abbiamo superato il limite... Un quiz nato a fine ottocento che ha visto la partecipazione di milioni e milioni di appassionati. Oggi, temo che il numero delle risposte esatte diminuirebbero di molto, tranne che da noi...