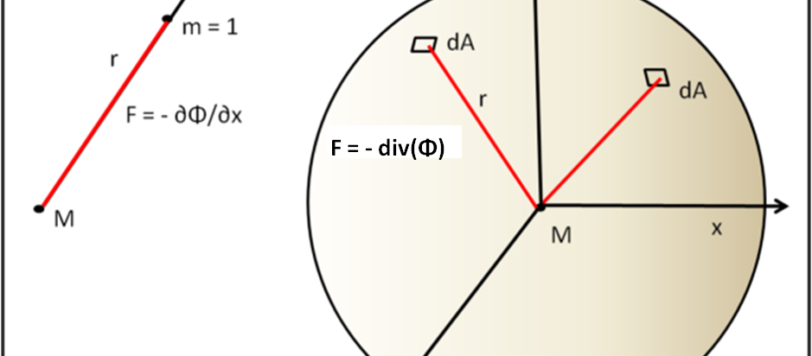
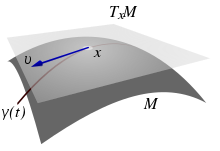
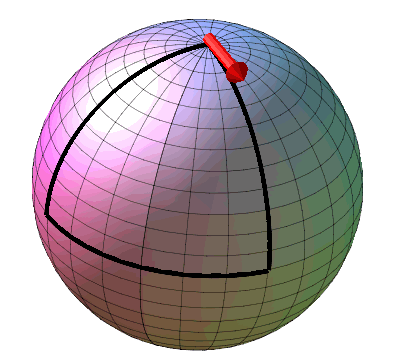
E' venuto il momento di iniziare a spostarci a destra del segno di uguale. Ci stupiremo, forse, che Einstein non annulla assolutamente la legge di Newton, ma la usa proprio per introdurre delle analogie per il caso in cui la curvatura è trascurabile. Einstein giudica Newton un grande che non poteva andare oltre e quindi prende il suo pennello e continua nell'opera d'arte ancora incompiuta. Così come Masaccio ha raccolto quello di Giotto...
Con le geodetiche e con il vettore tangente a loro, siamo pronti a descrivere lo spaziotempo curvo. Non resta che determinare come l'energia e tutte le sue forme (non solo la massa) lo possano deformare. Abbiamo tutti mezzi per descrivere ciò che l'energia ordinerà alla spazio tempo di fare. Newton diventerà nuovamente indispensabile.
Una delle parti sicuramente più ostiche, ma più che necessaria per arrivare, finalmente, al tensore di Ricci e saper trattare in modo quantitativo uno spaziotempo curvo.
Affrontiamo una delle parti più ostiche, facendola, però, seguire da alcune considerazioni e riflessioni molto più semplici.
Facendo viaggiare un vettore su una superficie sferica si può definirne la curvatura.
Questa parte è decisamente molto ostica e non tutto può essere ricavato nei limiti imposti al Circolo. Malgrado si debba prendere per buona una certa dimostrazione, la trattazione ha dei risvolti non banali, al limite della professionalità. Di meglio non riesco a fare...
Partendo dal teorema di Pitagora sul piano arriviamo a quello su uno spazio curvo, grazie al tensore metrico... le cose si complicano e le sommatorie si affollano.
E' ora di trasformare i tensori e di introdurre, in modo estremamente didattico, le coordinate controvarianti e covarianti. Le cose si complicano un poco e devo limitarmi a dare alcune definizioni ...
Introduciamo nuovamente i tensori, tenendo ben presente che abbiamo lavorato tanto per riuscire a manipolare correttamente le loro coordinate, cambiando sistema di riferimento. Ci aspetta un bel ... "lavoro"!
Abbiamo definito il valore di un "campo" in un certo sistema di riferimento. Questo valore deve, però, non dipendere dal sistema usato e perciò è necessario imparare a trasformare le coordinate di un sistema in quelle di un altro sistema. Facciamo il primo passo in tal senso.
E' venuta l'ora di entrare in un campo e. dato che è molto irregolare, vogliamo associare a ogni suo punto lo scostamento rispetto a un livello costante. In altre parole, associare a ogni punto il valore del campo. Lo facciamo a piccoli passi spostandoci di poco in ogni direzione. Alla fine otteniamo una "mappatura" tridimensionale perfetta. Ci accorgiamo che anche l'aggettivo "tridimensionale" perde di significato...
Pima di entrare nella formula vera e propria riassumiamo alcuni concetti che ci accompagneranno lungo tutto il viaggio.
Eccoci arrivati al dunque... Sono stato per un attimo incerto se iniziare questa avventura oppure no. Poi ho deciso per il SI e vada come vada. Potremo sempre interromperla e non pensarci più. In ogni modo, tra un virus e un problema burocratico e/o casalingo, mi sono divertito!
Ho deciso di provarci ... non so quanto tempo ci metterò, dato che ultimamente mi scappa via velocemente (sarà cambiata la curvatura?). L'approccio che tra poco vi descriverò è anche legato alla richiesta di Frank che vuole sapere tutto sulle onde (non pensavo che i facoceri fossero così curiosi!). Vi sono però alcuni concetti da digerire piuttosto bene che, in questo "prologo", cercherò di mettere in luce in modo molto semplificato e generale. Forza (o -meglio- curvatura) e coraggio!