Potevamo fermarci con l’articolo precedente. Tuttavia, non è male introdurre un QUIZ molto istruttivo. Anche senza tentare di risolverlo, è utilissimo seguirlo passo dopo passo. La soluzione alla prossima puntata.
Non ce ne sarebbe nemmeno bisogno, dato che la soluzione è stata “azzeccata” praticamente da tutti quelli che hanno risposto (chi subito, chi con un paio di passaggi). Tuttavia, la ripropongo velocemente.
Questo articolo vuole solo essere un piccolo assaggio di quello che un giorno vorrei descrivere con molta calma e attenzione. Un legame strettissimo tra relatività ristretta e meccanica quantistica che ha portato a conseguenze quasi impensabili. Così, un piccolo stuzzichino, tanto per gradire...
Cosa c’è di meglio di un bel paradosso per fare un po’ di ripasso della relatività ristretta? Ne presento uno che è alla base di tutta la rappresentazione grafica di Minkowski. Forse è stato proprio lui a dare il via al celebre diagramma.
Fatemi arrivare al dunque in modo molto personale e “quasi” allegro e spontaneo. Abbiamo incontrato lungo il percorso nuove grandezze che dipendono dalla velocità. Grandezze che cambiano, cambiando sistema di riferimento. Ciò che viene conservato sono le loro leggi di … conservazione. D’altra parte siamo o non siamo nella relatività ristretta? Tuttavia, pensandoci bene, qualcosa che non cambia c’è e questo fatto implica un nuovo invariante che lega l’energia con la mia grandezza preferita.
Le abbiamo studiate un po’ tutte, anche partendo solo dalla massa relativistica. Vale la pena, comunque, fare il procedimento inverso… (cosa che piacerà sicuramente a Umberto…), ossia dare per acquisita la formula dell'energia a riposo e vedere se, manovrandola adeguatamente, troviamo la massa relativistica.
Fermiamoci un attimo a riflettere per ricollegarci alla RR che abbiamo studiato fin dall’inizio. La celebre formula ci dice che l’energia dipende dal sistema di riferimento. Se sono solidale con il corpo in moto la sua energia è solo quella di riposo. Se sono in un sistema diverso, l’energia si separa in due termini e più la velocità aumenta e più l’energia osservata è praticamente solo quella cinetica.
Sbagliare è umano, ma perseverare è diabolico . Come se non bastasse la "chicca" dell'altro giorno, invece di cercare di aggiustare il tiro, si è proseguito sulla stessa strada, peggiorando la situazione. Per cercare di non ammettere i propri errori (non so se in buona o cattiva fede) si è arrivati a “pasticciare” non solo il paradosso dei gemelli, ma tutte le basi della RR. Sfruttiamo questi "orrori" per richiamare un esercizio che avevamo fatto descrivendo lo spazio di Minkowski, che dimostra la totale incomprensione del fenomeno.
Dimostrato che nella relatività ristretta è necessario modificare la definizione della quantità di moto, affinché essa si conservi, imponendo che la massa del corpo in oggetto aumenti con la velocità, risulta chiaro che le leggi di Newton devono subire delle modifiche strutturali, quando le velocità diventano paragonabili a quelle della luce. Non saltate questo articolo, mi raccomando... E' quello che , finalmente, ci porterà per mano alla più celebre formula della fisica.
Abbiamo appena iniziato la dinamica relativistica, ma forse è bene cominciare a misurarsi con lei e con la sua importanza globale che non è minimamente scalfita dalla sorella più giovane, ossia la relatività generale.
Chi vuole divertirsi ancora un po’ (è del tutto facoltativo) può arrivare alla stessa conclusione, utilizzando il ragionamento fatto da Feynman. E’ sicuramente un metodo più rapido, senza formule noiose, ma comporta un ragionamento finale sul risultato che potrebbe causare una qualche confusione nei meno attenti e concentrati. Sicuramente, è geniale come tutto ciò che ha fatto lui…
Abbiamo deciso di cambiare la definizione di quantità di moto. Dirlo è una bella cosa, ma farlo è un’altra. La soluzione migliore sembrerebbe quella di considerare la massa come una funzione della velocità. Non abbiamo certo detto una cosa da poco. Basterebbe pensare che ciò vorrebbe dire che l’inerzia di un corpo cambia al variare della sua velocità. Teoricamente potrebbe diventare infinita. Non ci resta che fare questo tentativo e controllare, con molta attenzione, se questa sconvolgente ipotesi riesce, veramente, a conservare la nuova quantità di moto. Questo articolo è il più “duro”, ma niente di veramente difficile.
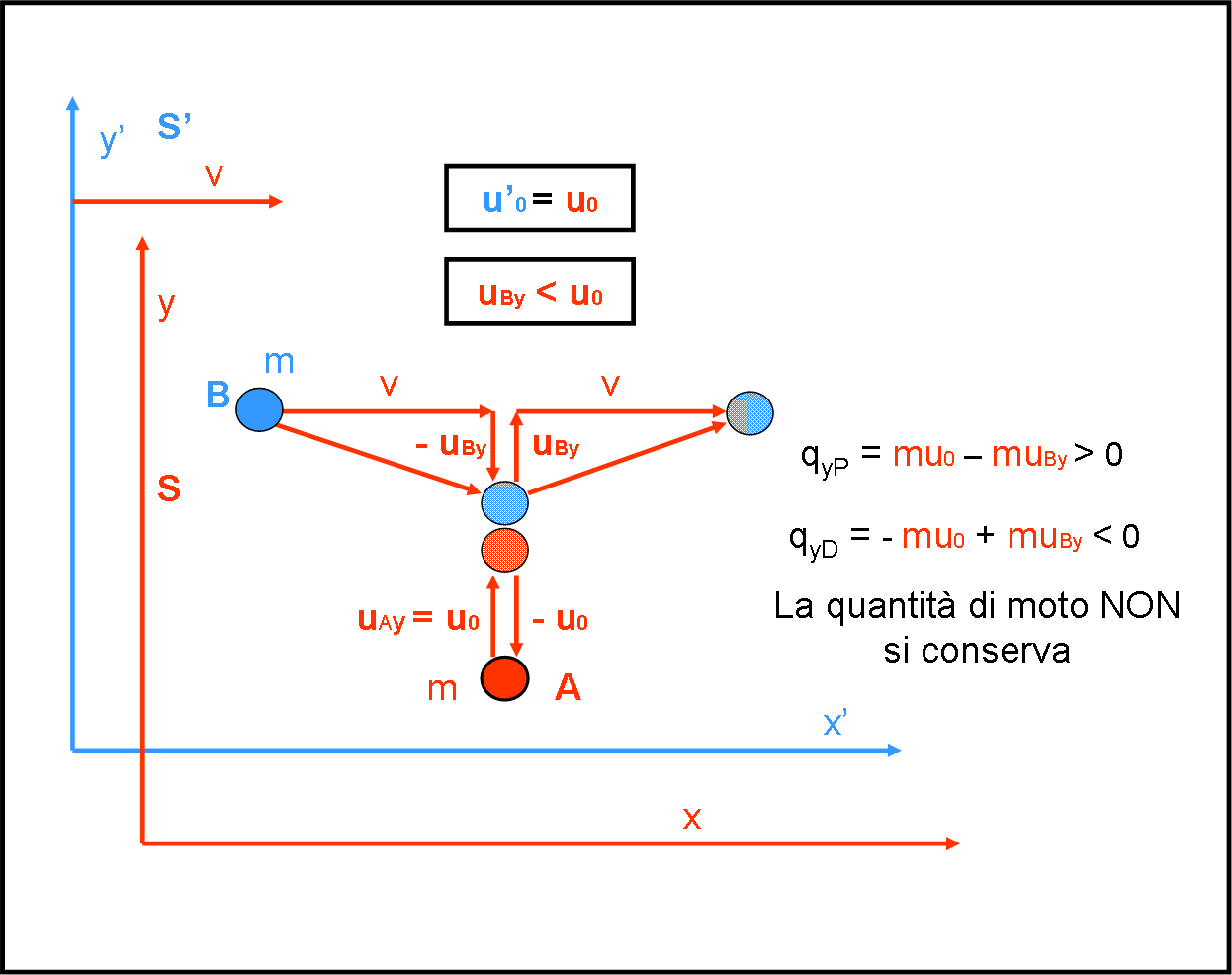
Questo articolo è molto corto. Preferiamo mangiare la “torta” a piccoli tranci per permetterci di gustarla fino in fondo. Dimostrare che la quantità di moto “classica” non si conserva nella Relatività Ristretta è un punto di arrivo fondamentale e va compreso perfettamente bene. Una conclusione, in realtà, banale, ma che ci obbliga a modificare tutta la dinamica conosciuta fino ad allora. Ricordiamo, comunque, che stiamo parlando di velocità comparabili a quella della luce. Se giocassimo a palline con un nostro amico che va in bicicletta niente cambierebbe rispetto alle descrizioni di Galileo.
Siamo pronti per partire con la dinamica relativistica. Per far ciò è fondamentale descrivere, prima di tutto, come la quantità di moto sia costretta a cambiare per potersi conservare. Normalmente questa parte si dà per assodata o si spiega -spesso- in modo poco chiaro, incentrando tutto sulla massa relativistica, gioia e dolore dal punto di vista concettuale. Ho cercato di raggiungere lo scopo nel modo più semplice possibile, evitando, però, semplificazioni che avrebbero generato eventuali confusioni. Ho deciso di pubblicare questa parte iniziale della dinamica relativistica (DR) prima della fine degli integrali, in quanto non ne ha bisogno. Vi prego sinceramente di esporre tutti i dubbi senza paura. Ricordiamoci che senza questa base di partenza i nodi verrebbero, comunque, al pettine più tardi… Fatemi anche capire (in tanti) se … avete capito! Basta un OK...
A qualcuno potrebbe sembrare che io stia sollevando un sacco di problematiche concettuali e di ostacoli, nel tentativo di descrivere correttamente la quantità di moto relativistica. In giro per la rete si trovano determinazioni velocissime e che -a prima vista- sembrano del tutto logiche… sicuramente più rapide e semplici del procedimento che ho iniziato a descrivere con molta precauzione. Attenzione, però...
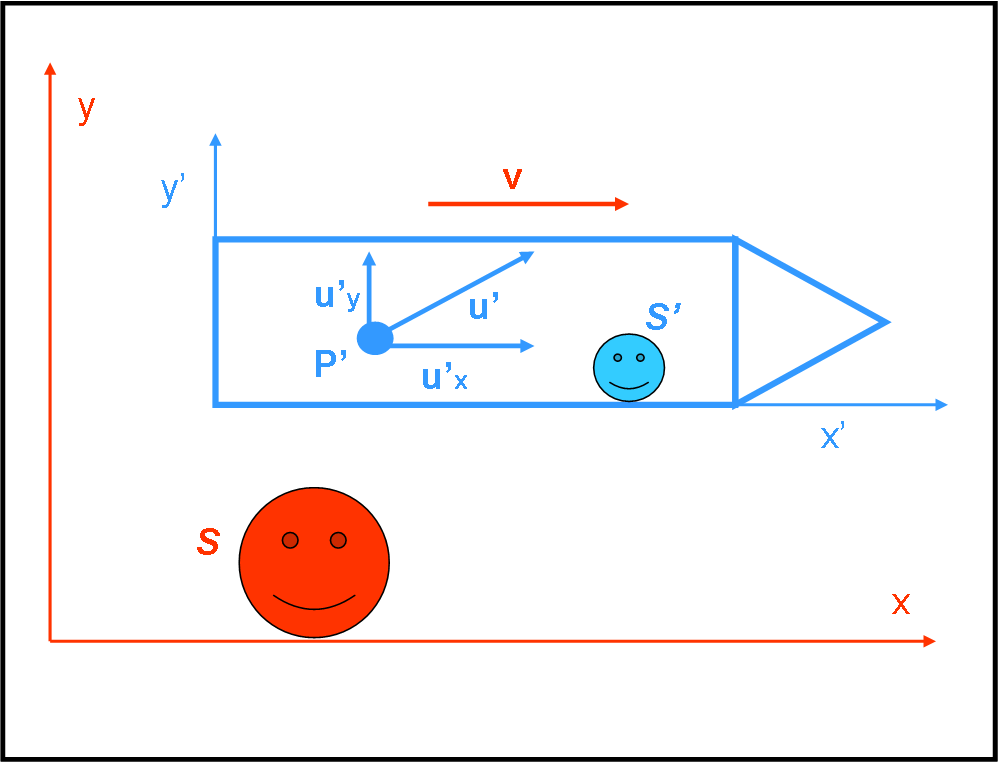
Divertiamoci un poco, preparandoci alla dinamica relativistica. Ho deciso (molto democraticamente...) di iniziarla prima di completare gli integrali, dato che la parte riguardante la quantità di moto non ne ha bisogno. L’argomento di questo quiz ne costituisce una specie di introduzione. Tuttavia, dato che riguarda la composizione delle velocità relativistiche, che avevamo già trattato in due articoli, siete in grado di risolvere il problemino da soli… La risposta sarà proprio l’inizio del primo articolo ufficiale. Ah... non illudetevi, però: gli integrali continueranno...

