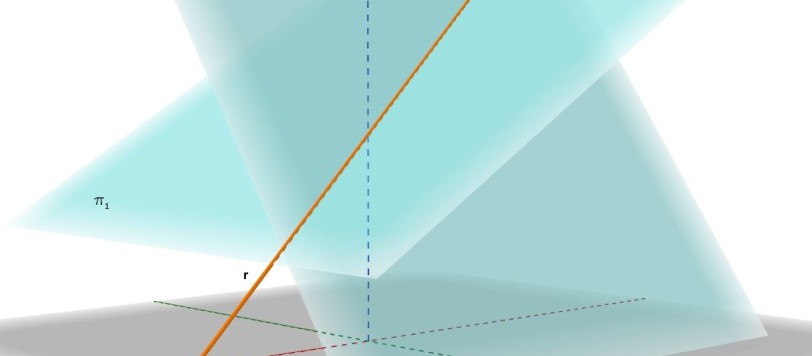
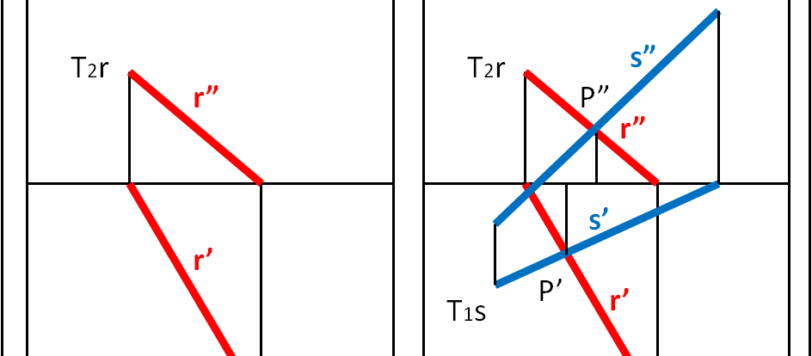
Continuiamo con il metodo descrittivo di Monge e proiettiamo una retta nel caso più generale e in alcuni casi particolari.
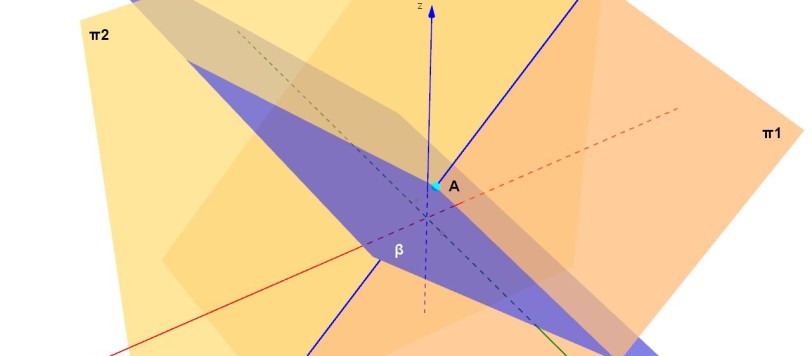
Nel precedente articolo, che potete rileggere QUI, ho introdotto il concetto di parametri direttori di una retta nel piano. In questo estendiamo il concetto alla retta nello spazio e al piano. Passiamo, quindi, nel riferimento cartesiano dello spazio.
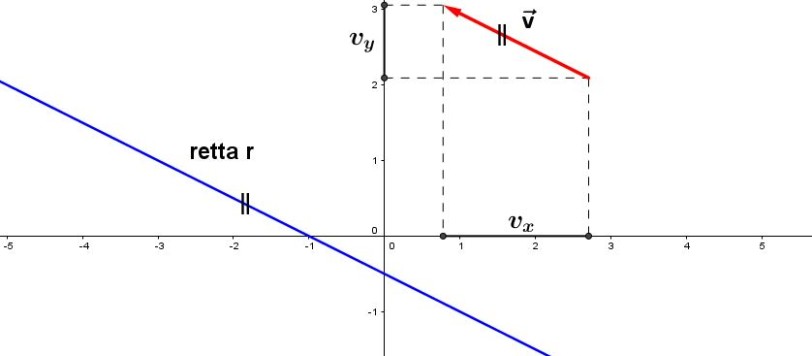
In questo articolo e in quello successivo intendo illustrare un elemento sinora da me mai citato ma che , come vedremo, si rivela molto utile nella trattazione di problemi di geometria, in particolare quella dello spazio. Tale elemento caratterizza una retta, indicandone la direzione, oppure un piano, consentendoci di individuarne subito tutte le infinite rette ad esso perpendicolari. Scopriremo che sia la retta sia il piano si "portano dietro" questo elemento come una targa identificativa, che a noi basta quasi leggere per conoscere subito, in termini analitici, la direzione della retta o la giacitura del piano.
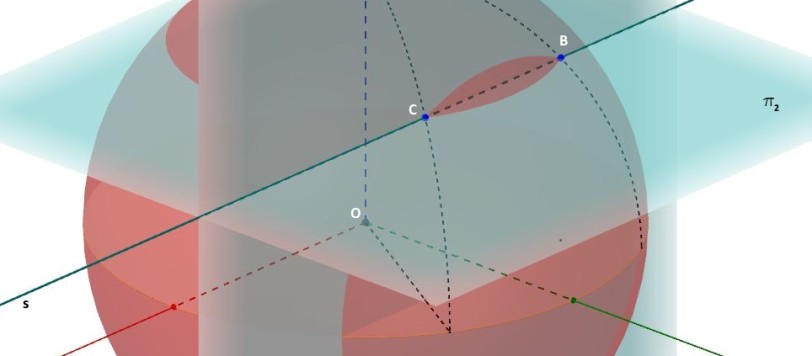
Dopo il primo articolo sulla geometria solida, pubblicato in due parti QUI e QUI nelle scorse settimane, eccoci ora giunti a questa appendice. In essa, mettendo in pratica i concetti di geometria solida sinora esposti, con particolare riferimento al piano, al fascio proprio di piani e alla sfera, dimostreremo che, dati due punti su una […]
Proseguiamo il nostro percorso nella geometria dello spazio con la seconda parte dell'articolo. La numerazione delle figure e delle formule segue quella della prima parte dell'articolo, che trovate QUI. Fasci di rette nel piano e fasci di piani nello spazio Nel piano le rette posso essere tra loro incidenti, quando hanno un punto in […]
Obiettivo di questo articolo, di cui viene pubblicata ora la prima parte, è quello di entrare nell'affascinante mondo della geometria dello spazio e, dopo la seconda parte, dimostrare che la curva congiungente due punti situati su una superficie sferica e che misuri la minore distanza tra essi è un arco di circonferenza massima, ossia avente centro coincidente con quello della sfera.
E’ ora di tornare alla nostra matematica, dato che molti l’hanno seguita e vorrebbero proseguire. Abbiamo iniziato a studiare le funzioni e torniamo improvvisamente indietro a parlare di nuovo di retta, la funzione più semplice e la prima che abbiamo trattato… Sembrerebbe una cosa assurda.
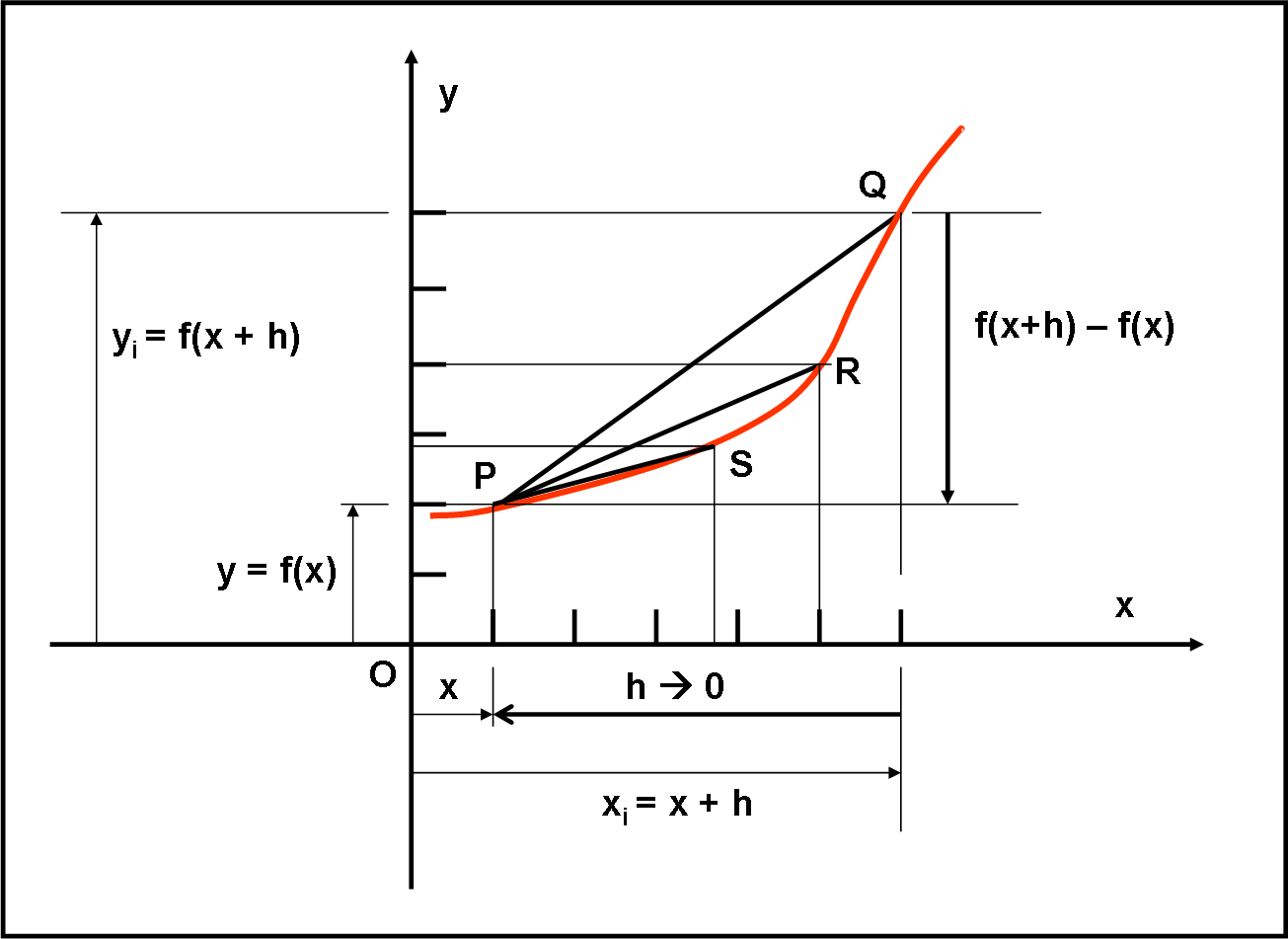
Siamo arrivati a un punto fondamentale: l’introduzione della derivata di una funzione. Iniziamo col descriverla in modo estremamente semplificato, quanto basta per afferrare il concetto base. Poi, compresa la sua ragione di esistere, vedremo di utilizzare la matematica che già conosciamo per utilizzarla al meglio. Un passo alla volta. Ho usato una strada lunga e ho girato molto attorno al problema. L’ho fatto sperando di semplificare. Tuttavia, questo è forse l’articolo più importante per entrare nel mondo della matematica “superiore” e, quindi, comunicatemi ogni pur piccolo dubbio abbiate e cercherò, se necessario, anche di cambiare la trattazione se per qualcuno risulta ancora difficile. Scrivo queste “lezioni” per voi e quindi aiutatemi a migliorarle… mi raccomando! Come al solito, ho reso l’articolo simile a un’avventura… un’avventura “matematica”, ovviamente!
Se la volta scorsa vi avevo “martellato” duro, questa volta vi vengo incontro. Poche righe per definire le coniche in un modo matematico ben più ampio e generale. Tuttavia, non andremo nei dettagli e ci limiteremo al concetto base. Chi ha, però, voglia di divertirsi ha tutti i mezzi a sua disposizione.
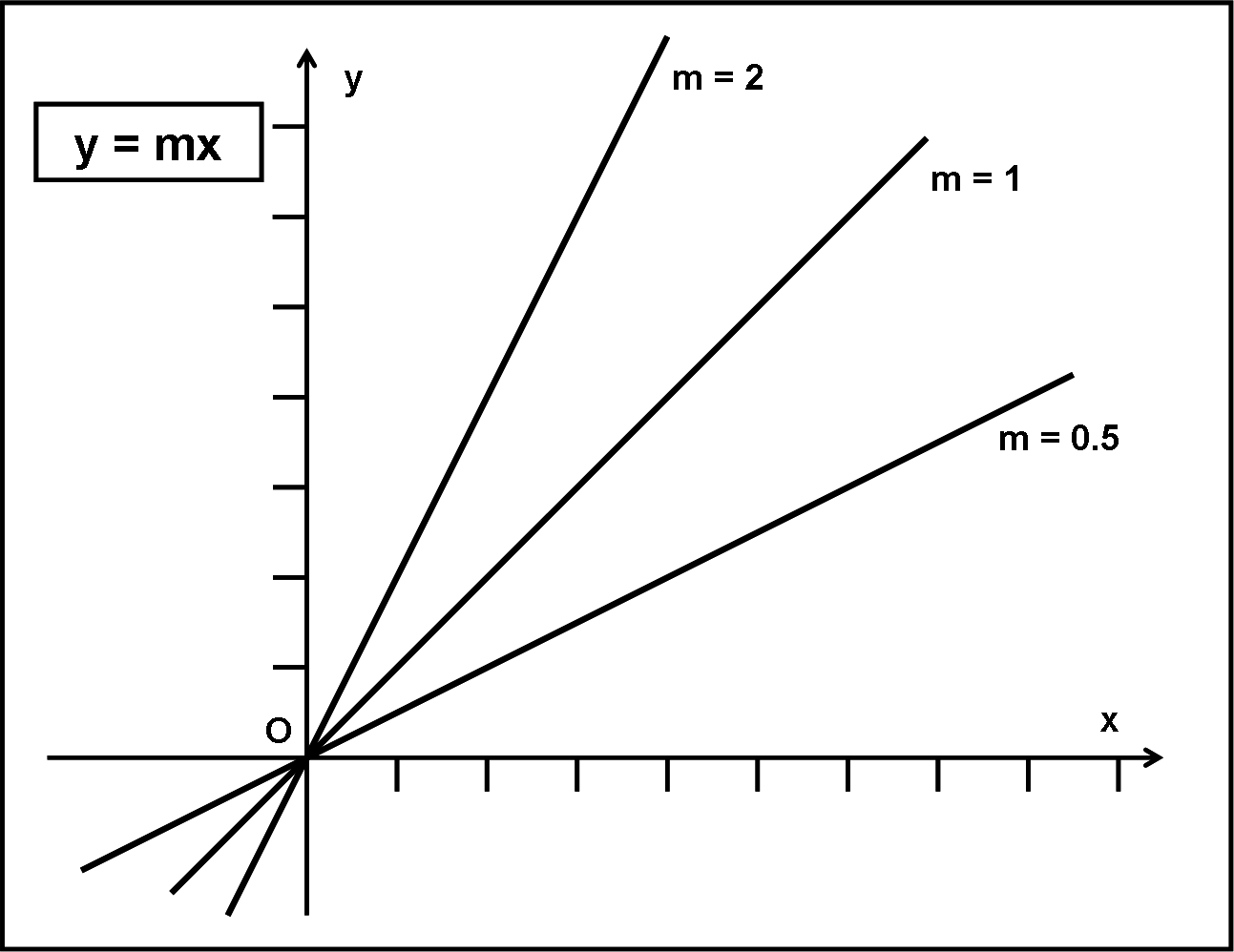
E’ giunta l’ora di introdurre le prime funzioni. Cominceremo dalla più semplice, ma vedrete che sarà più che sufficiente per farci chiacchierare molto a lungo e per capire meglio il concetto di infinito.
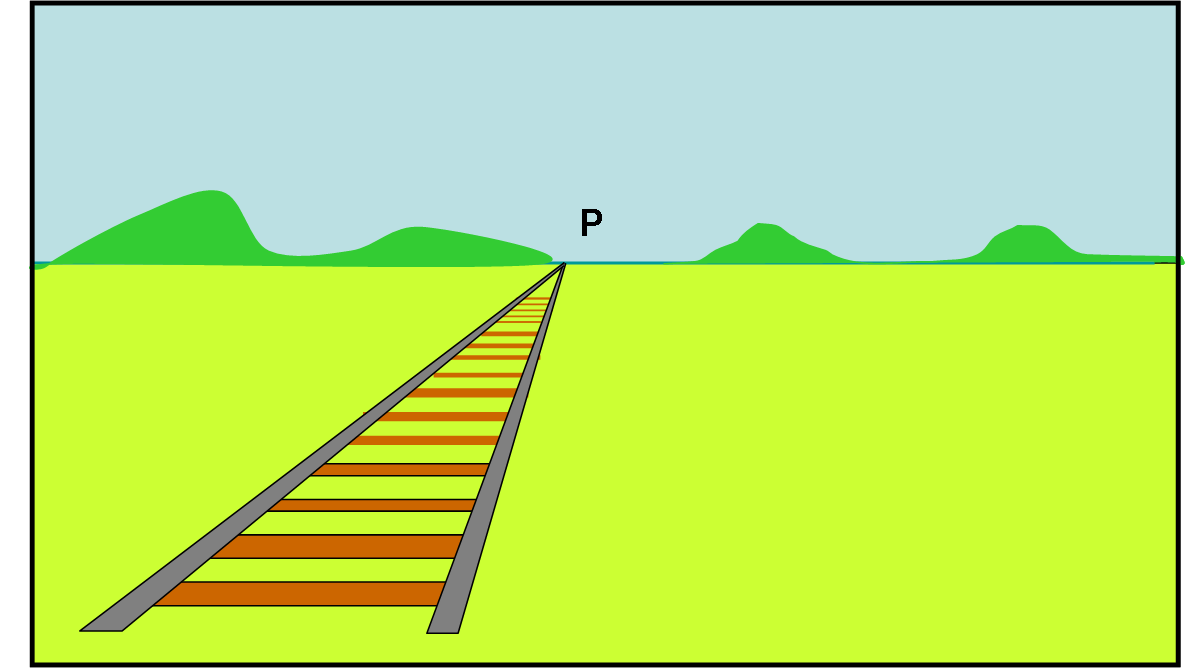
Ho cercato il modo migliore per introdurre due numeri (o -meglio- concetti) fondamentali per la matematica, la geometria e la fisica. Ho trovato varie possibilità, anzi potrei dire che ne ho trovato infinite. E, allora, mi sono fermato se no rischiavo di mordermi la coda (che non ho… ve lo giuro!). Ho quindi deciso di agire a modo mio. L’importante è che alla fine si riesca a comprendere con chi abbiamo a che fare.