Un quiz che si dimostrato più difficile del previsto... Eppure la dimostrazione puramente geometrica lavora quasi soltanto con angoli alla circonferenza. Il problema è forse l'introduzione della seconda circonferenza.
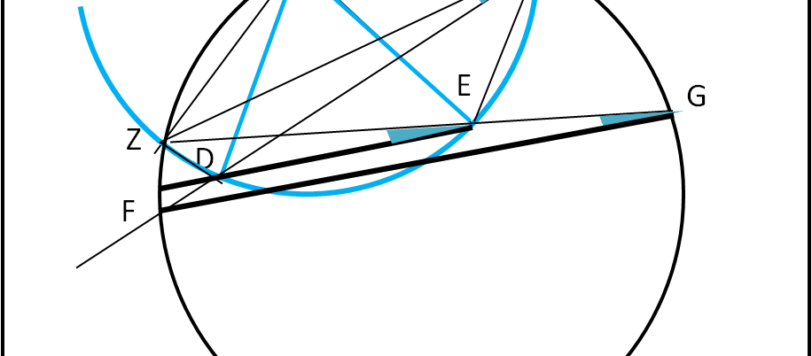

Un quiz che si dimostrato più difficile del previsto... Eppure la dimostrazione puramente geometrica lavora quasi soltanto con angoli alla circonferenza. Il problema è forse l'introduzione della seconda circonferenza.
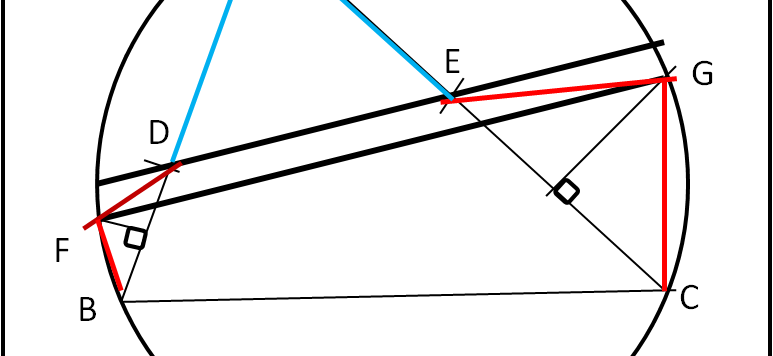
Lasciamo da parte le parabole (per adesso...) e torniamo ad una più semplice circonferenza e ad un triangolo in lei inscritto.

Il teorema di Talete porta con sé un po' di ambiguità, dato che quello che noi italiani chiamiamo "teorema di Talete" è diverso da quello "inglese". Dimostriamo quest'ultimo e ci accorgeremo che si devono dimostrare anche altri enunciati, che siamo soliti dare per buoni. Un'interessante modo per capire quanta logica ci sia nelle scoperte geometriche degli antichi greci (ma non solo loro, anche degli indiani, dei cinesi, degli arabi...)