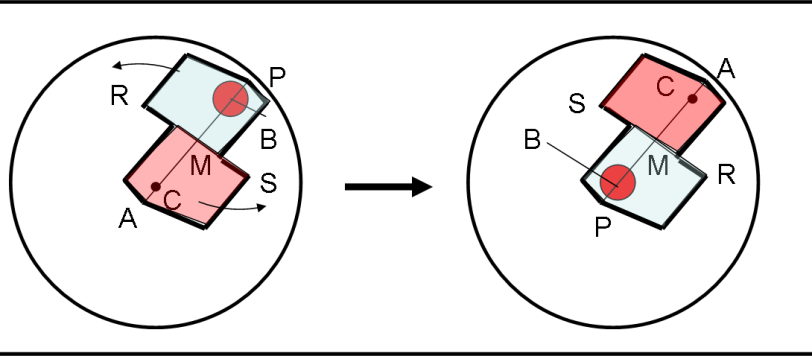
Bravissimi, come sempre, Andy e Fabrizio! Come soluzione riporto una versione puramente algebrica che prende spunto dalle medie aritmetiche e geometriche. La discussione resta comunque aperta...
Seconda parte dell'articolo sui quasi-cristalli, centrato sul concetto di simmetria.
L'intrigante argomento dei quasi-cristalli non può essere affrontato senza alcune necessarie premesse, relative alle basi teoriche della mineralogia e della cristallografia. Questo primo articolo intende illustrarne i concetti fondamentali; ad esso ne seguirà un secondo, focalizzato sulle strane peculiarità dei quasi-cristalli e sulla loro "impossibile esistenza" ed un terzo, conclusivo, che aprirà una finestra proprio su questa "impossibilità".
Il titolo è alquanto sibillino, ma vuol dire, in pratica, che se ci accorgiamo che la Natura rompe quella che noi consideravamo una perfetta simmetria, è molto facile che il modello da noi costruito sia sbagliato.
In questo articolo vi è la soluzione più semplice (senza calcoli sofisticati) sia della prima parte che della seconda, verso cui si era già scatenato un bel manipolo di concorrenti (Arturo, Leandro, Maurizio, Paolo Salvini, Pippo e Umberto). La seconda parte era trapelata nei commenti e riguarda il DOVE la volpe prende il coniglio. Esiste, comunque, una soluzione analitica della seconda parte, che abbisogna di integrali per passare da velocità a posizione, ma qui viene presentata quella tipica di una volpe, furba, decisa e senza tanti ghirigori…
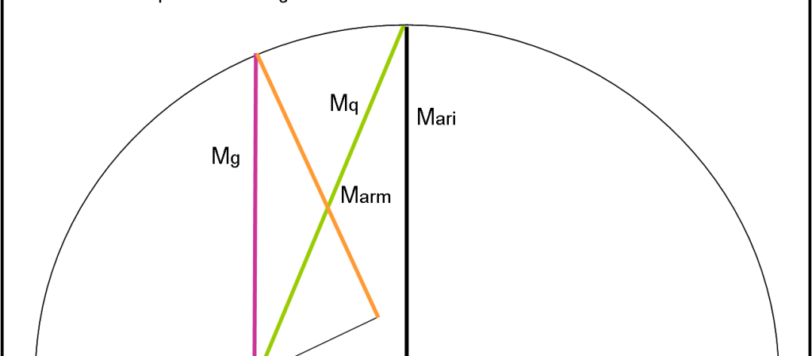
La soluzione è già stata data nei commenti, tuttavia (ormai mi conoscete bene) cerco di complicare le cose. No, niente di speciale, solo la ricerca della massima generalità nella soluzione.
Sappiamo bene che uno dei più grandi problemi collegati ai modelli che descrivono la nascita e l’evoluzione dell’Universo sta nell'enorme disparità tra materia e antimateria. In poche parole, non si capisce ancora perché la prima sembra aver vinto alla grande contro la sua sorella “speculare”. Tutto ciò che ha carica positiva dovrebbe esistere con carica negativa e viceversa. Non voglio entrare nei dettagli e tra poco capirete perché.
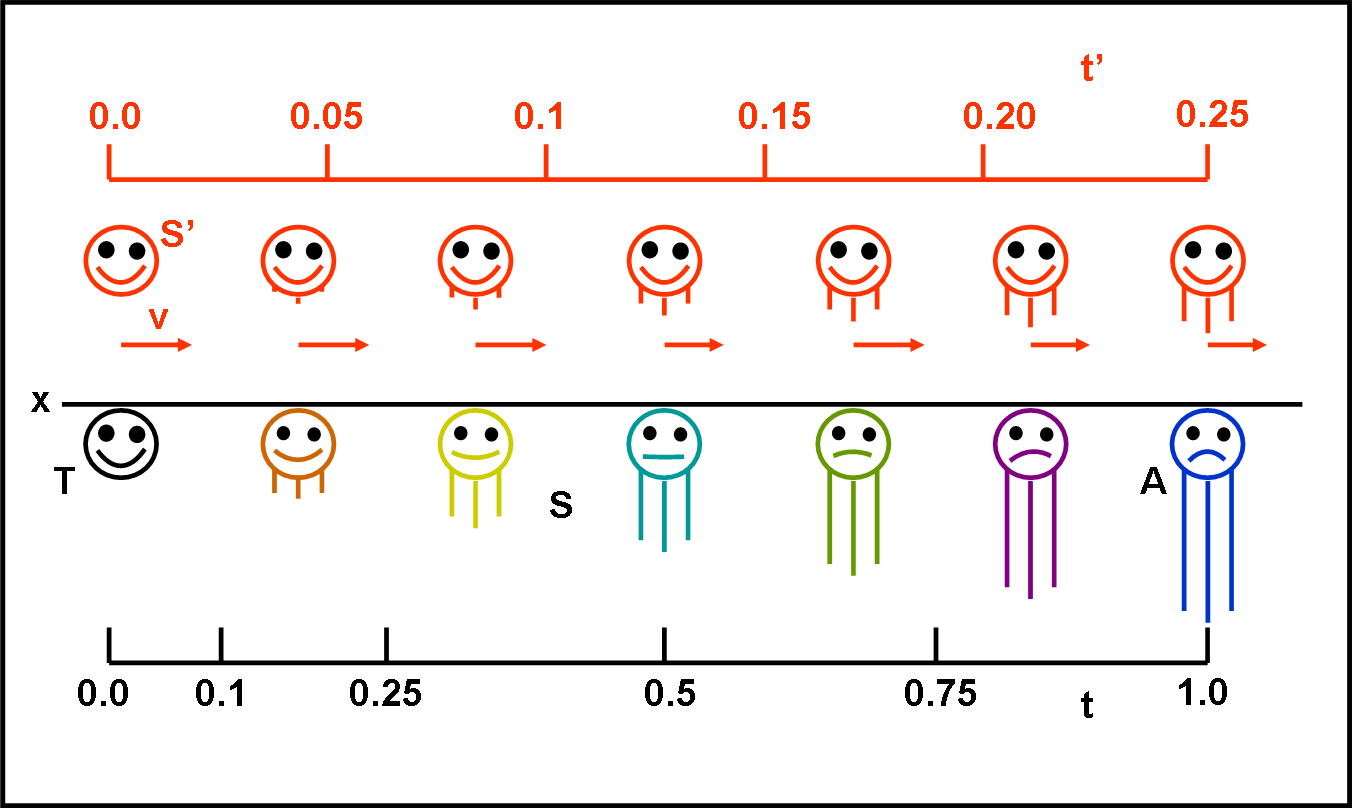
In attesa di proseguire con il diagramma di Minkowski, divertiamoci a impostare il paradosso dei gemelli che ci verrà molto utile per controllare se abbiamo compreso esattamente ciò che realmente capita quando si osserva un sistema in movimento. Proviamo a definirlo in modo molto semplificato, evidenziando alcuni punti che spesso non sono spiegati esaurientemente. Un piccolo esercizio senza pretese, ma che può chiarire molti dubbi e confusioni.
Avrei voluto completare l’intero passaggio da Galileo a Lorentz, ma sarebbe stato abbastanza lungo, soprattutto se spiegato con dovizia di particolari e di esempi (magari ripetitivi). Dato che, inoltre, alcuni concetti “preparatori” devono essere compresi perfettamente, e non sono così banali come possono sembrare a prima vista, inizio con una specie di “antefatto”. Infine, un passo in avanti piccolo piccolo permette di rimettersi in linea con quanto scritto “molto” tempo fa. Chi va piano va sano e va lontano…