La velocità più difficile da misurare? La velocità della luce. Lo sapeva anche Einstein e ha dovuto imporre una "convenzione" per sviluppare la sua teoria. E le cose non sono ancora cambiate...


La velocità più difficile da misurare? La velocità della luce. Lo sapeva anche Einstein e ha dovuto imporre una "convenzione" per sviluppare la sua teoria. E le cose non sono ancora cambiate...

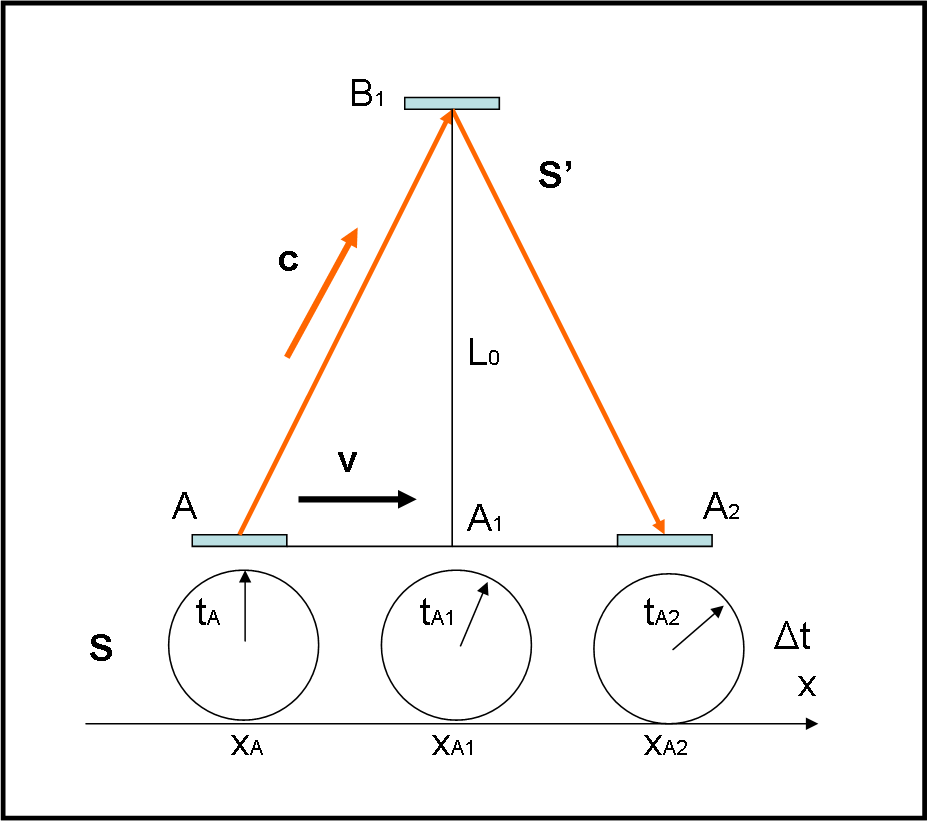
Dopo la dilatazione dei tempi, continuiamo con il semplice metodo di Epstein per descrivere la relatività ristretta. Questa volta tocca alla contrazione delle lunghezze e alla mancanza di sincronizzazione di orologi in moto relativo. Applichiamo, infine, il metodo per via puramente grafica per ritornare, ancora una volta, sul paradosso dei gemelli.
Questa è la prima parte della Teoria della Relatività Ristretta o Speciale. Si parte dalla relatività galileiana e si arriva agli effetti che derivano dai postulati di Einstein: dilatazione dei tempi e contrazione delle lunghezze. Facciamo conoscenza con la trasformazione di Lorentz , il passo fondamentale per passare da spazio e tempo a spaziotempo. Ricordiamo che l'intera teoria si riferisce SOLO a sistemi di riferimento in moto rettilineo uniforme tra loro. Non sono quindi valutate le deformazioni spaziotemporali causate dalla gravità e dalla sua accelerazione. La relatività ristretta è quindi una teoria perfettamente simmetrica e niente ha a che vedere con le deformazioni univoche causate dalla relatività generale. Negli articoli seguenti, si toccheranno le ripercussioni della relatività ristretta sulle varie grandezze fisiche (tra cui la celebre E = mc2) e la sua rappresentazione nel diagramma spaziotemporale di Minkowski.
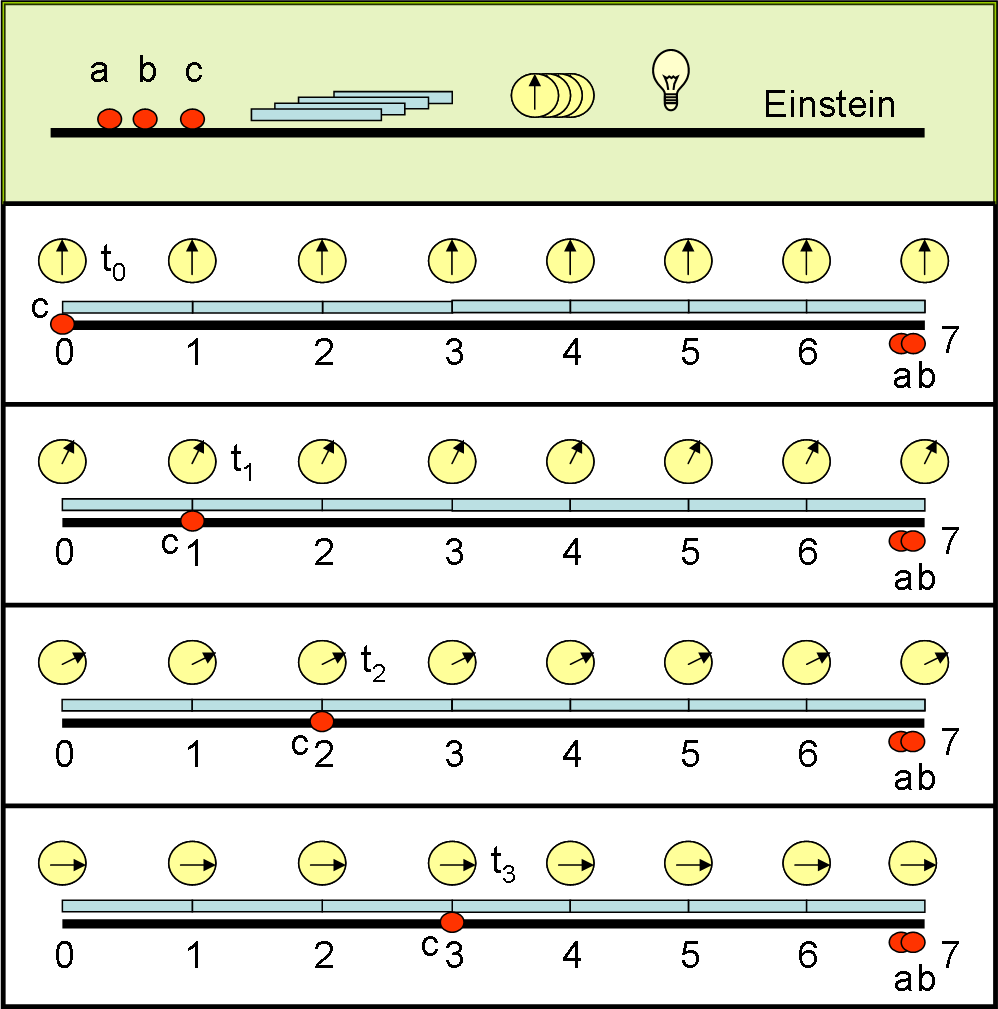
Iniziamo, lentamente, la descrizione e le varie conseguenze della relatività ristretta. Dopo un piccolo esame fatto a Newton e a Einstein, affrontiamo un argomento che sembra banale ma che è, invece, concettualmente, tra i più complicati : la simultaneità di due eventi. Senza dimenticare di sincronizzare gli orologi…