Eccovi la mia soluzione che vuole essere un esercizio di fisica (poca) e tanta matematica (in particolare trigonometria). Come già detto, si può probabilmente sveltire il procedimento, ma non è certamente sbagliato.


Eccovi la mia soluzione che vuole essere un esercizio di fisica (poca) e tanta matematica (in particolare trigonometria). Come già detto, si può probabilmente sveltire il procedimento, ma non è certamente sbagliato.

Questo articolo risponde alla richiesta per la costruzione delle reti autostradali ottimali. Vediamo di fare i vari calcoli e di introdurre un nuovo tipo di percorso minimo.
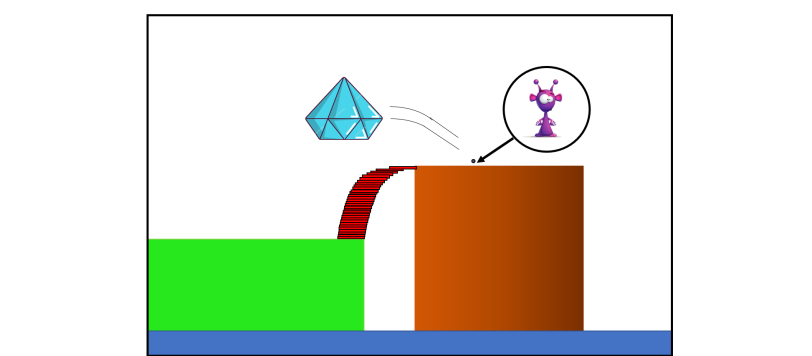
Andiamo a vedere come la nostra formica viola ha risolto il problema dello scoglio e si è impossessata del magnifico diamante.
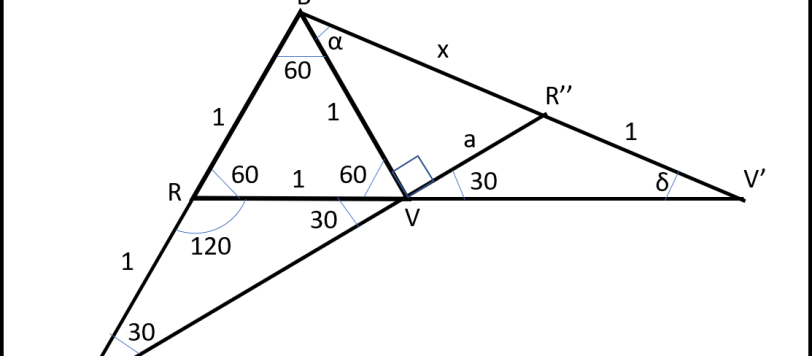
L'esercizio va risolto solo con la trigonometria. Ciò non toglie che alla fine si ottenga un'equazione di quarto grado, la quale, però riesce a essere risolta con estrema facilità. Un bravo a Fabrizio...
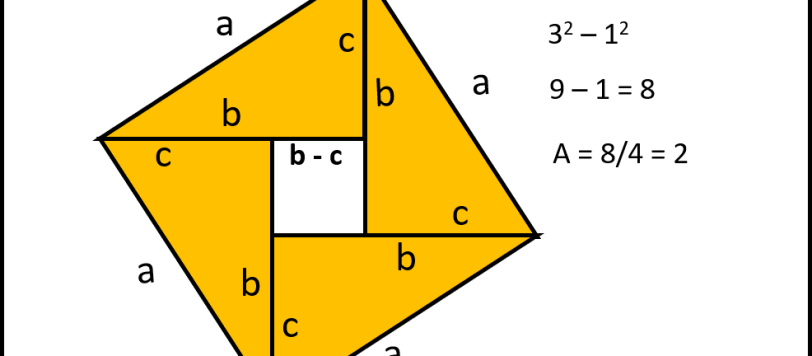
Grazie a Daniele il nostro triangolo è riuscito a calcolare la propria area. Adesso speriamo che prosegua nelle studio delle sue proprietà geometriche che sono tante e strabilianti...

Questo articolo, oltre a dare la soluzione più rapida al problema posto qualche giorno fa, ci mette di fronte a una divertente soluzione seguita da un paio di matematici cinesi che sono riusciti a scalare l'Everest per andare da un villaggio a un altro, uniti da una breve e comoda superstrada... In altre parole: come complicare le cose semplici... Non perdetevelo!

Innanzitutto un bravo a Fabrizio e alle sue trattazioni, che trovate nei commenti del quiz. Ricordiamo, poi, che questa è praticamente la risposta al quiz sulla formica, ma è anche un articolo tutto da leggere, soprattutto per le sue implicazioni finali e per l'utilizzo della serie armonica. Un paradosso che viene ancora una volta risolto, anche se necessita di tempo, tanto tempo...
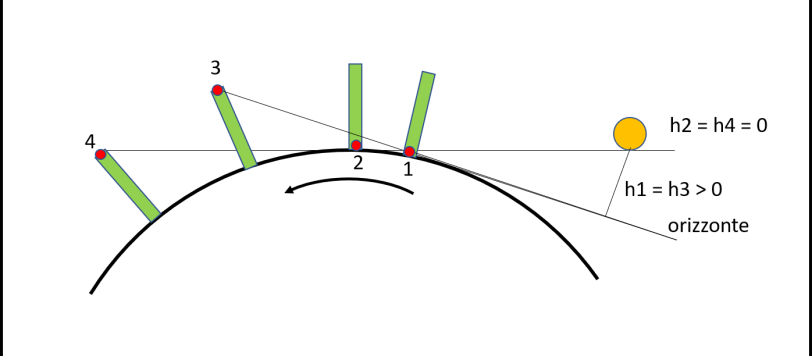
E' solo una questione di orizzonte... Non potendo muoversi sulla superficie terrestre bisogna alzarsi! Ma farlo in modo molto veloce lottando e vincendo contro la velocità di rotazione terrestre.
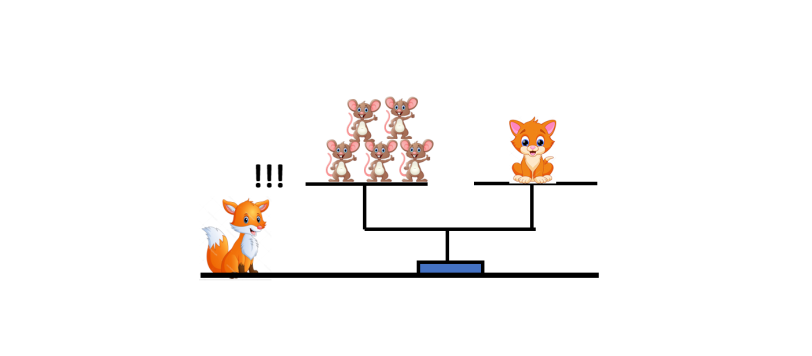
Diamo la soluzione al quiz che vedeva coinvolti tanti cuccioli (gattini, topini, cagnolini e leprotti) e una furba volpacchiotta. Seguiamo il ragionamento di quest'ultima...
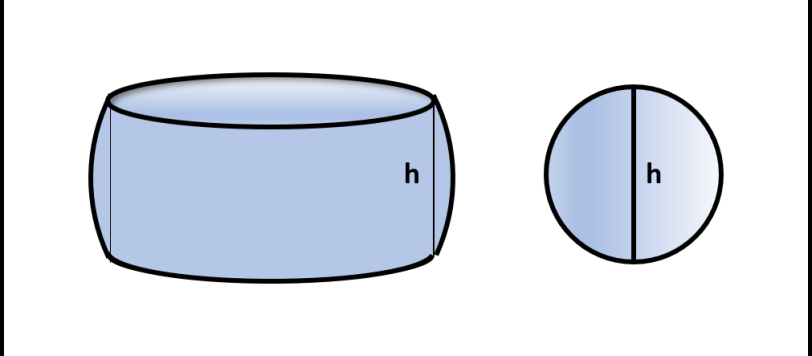
In questo ultimo articolo riguardo a Mamikon risolviamo, con il solo "calcolo visuale" , il problema relativo alla talpa spaziale. Possiamo dire di avere introdotto il teorema di Mamikon ... tridimensionale!
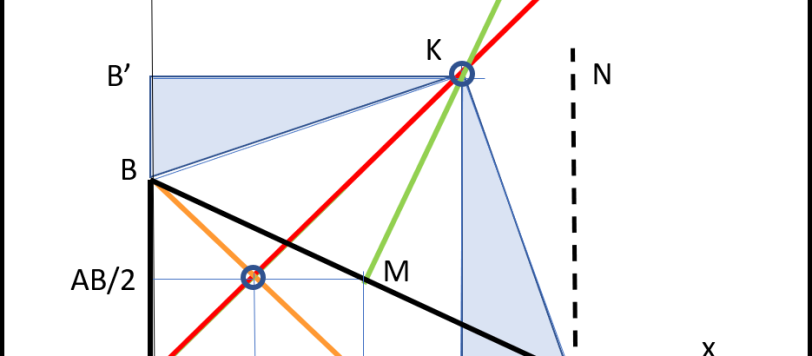
Ebbene sì, tutti i triangoli non possono essere isosceli o equilateri. Per provarlo basta non fare disegni SBAGLIATI.
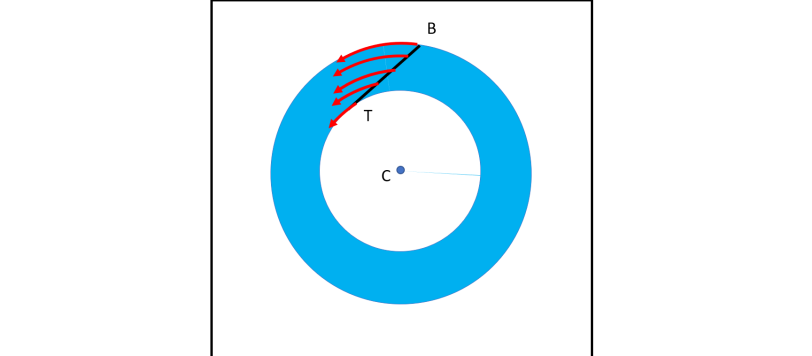
Questo articolo non riporta solo la soluzione al primo di due recenti quiz, ma vuole descrivere molto di più e, quindi, non perdetevelo! La geometria può diventare una specie di romanzo d'avventura... Potremmo chiamarla "geometria dinamica"!
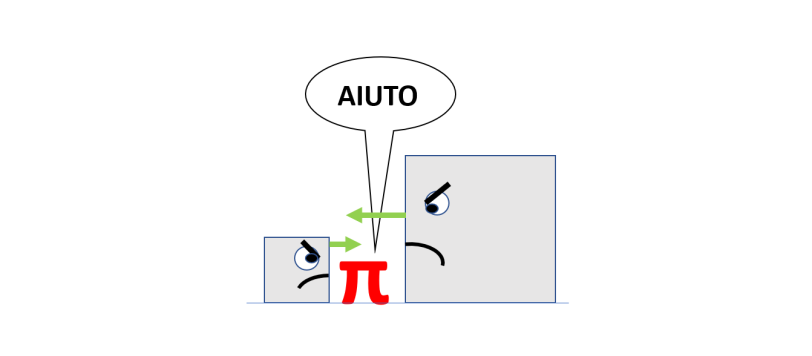
Abbiamo visto che gli urti tra due masse e di una di loro contro una parete riesce a regalarci le cifre significative del pi greco. Analizziamo a fondo il perché, anche se Francesco ha già dato una risposta esauriente. Ci troviamo di fronte a un problema puramente matematico espresso attraverso la meccanica e dimostrabile con la semplice geometria. Un gran bell'esempio di interdisciplinarità.
La prima parte, ossia quella relativa a cosa "saltava fuori" era decisamente facile, anche se molto noiosa...