Bravi i nostri solutori, anche se il 495 e il 6174 rimangono ancora avvolti nel mistero. Certo è che ancora una volta domina il numero 9.
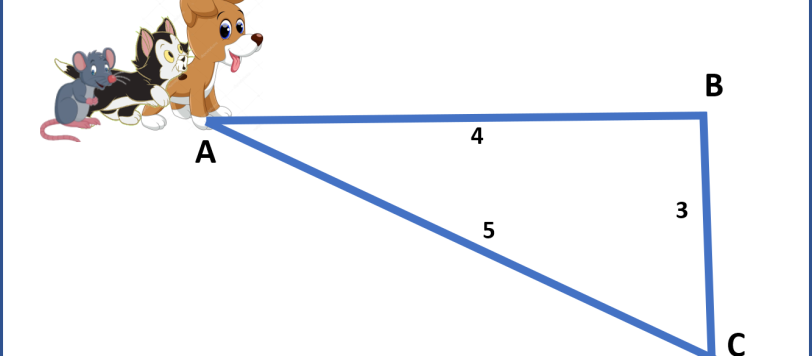
Il problemino sembra subito più difficile di quanto non sia in realtà. Basta ricordarsi che per determinare gli angoli di un triangolo è sufficiente conoscere le dimensioni relative dei lati (come dice Guido).
Qui trovate il quiz e i commenti. Presento la mia soluzione in modo un po' più formale. Questo per dare una spiegazione in più; già leggendo i commenti di Vincenzo (e anche di altri) si riesce a giustificare la soluzione in modo intuitivo-geometrico.Mi baso su una figura, che è un caso semplificato del nostro problema. […]
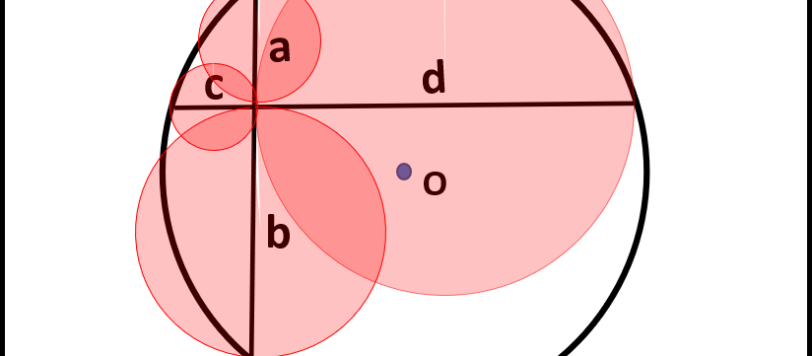
Ecco la soluzione puramente geometrica, anche se, come sempre, il risultato si poteva ottenere in modo analitico.
La soluzione è più facile di quello che si potrebbe pensare. In realtà, il numero infinitesimo di secondi di ritardo al secolo farebbe pensare a un effetto altrettanto microscopico sullo spostamento delle coordinate stellari... e, invece, superiamo di gran lunga le previsioni.
Una domanda oltremodo facile a cui è già stata data la risposta attraverso i commenti. Comunque, affrontiamo la risposta compiutamente.
Un esercizio veramente banale per chi ha capito la relatività ristretta e il diagramma di Minkowski, in particolare. Io, come spesso amo fare, lo risolvo in modo puramente geometrico.
Come già detto, in fisica esistono molto spesso procedimenti diversi per risolvere un certo problema. La soluzione che riporto io potrebbe anche non essere la più rapida. La difficoltà dell’esercizio sta nella stretta relazione esistente tra il moto del cubo e quello del cuneo (e viceversa). Una sola forza si scompone e si ricompone intrecciando le accelerazioni finali dei due corpi in movimento.
La soluzione che propongo io è sicuramente molto lunga, ma ha lo scopo di richiamare molti concetti importanti del moto parabolico.
L'orologio a luce messo in orizzontale ci dona subito una risposta positiva... ma anche il grande amico Minkowski.
Come anticipato, il problema è decisamente facile e ha il solo scopo di richiamare la differenza che esiste tra baricentro geometrico e centro di massa.
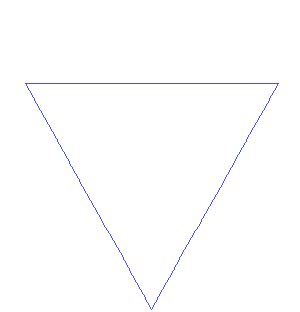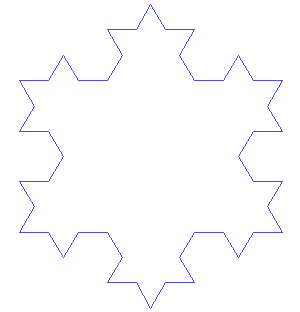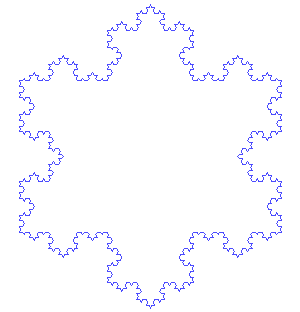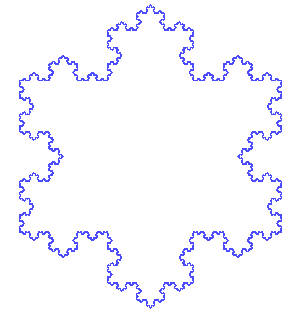
L'isola che non c'è, in realtà, c'è ed è legata ad una delle prime curve frattali proposte, ben prima che i frattali fossero introdotti e studiati con grande attenzione. Tutto il quiz è stato "montato" per potere parlare delle sue caratteristiche veramente speciali.
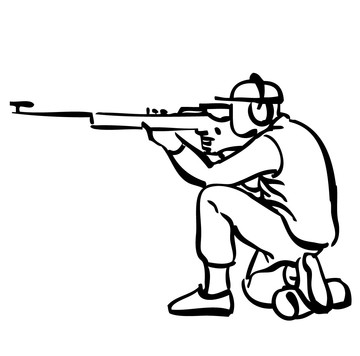
Il quiz, pur se leggermente romanzato, è uno dei tipici esercizi di Fisica classica che si incontrano quando si studia la quantità di moto. In particolare, la legge di conservazione della quantità di moto nel caso di sistemi isolati. Il sistema costituito, nel nostro caso, dalla barca con sopra il soldato e dall'ambiente circostante (acqua […]
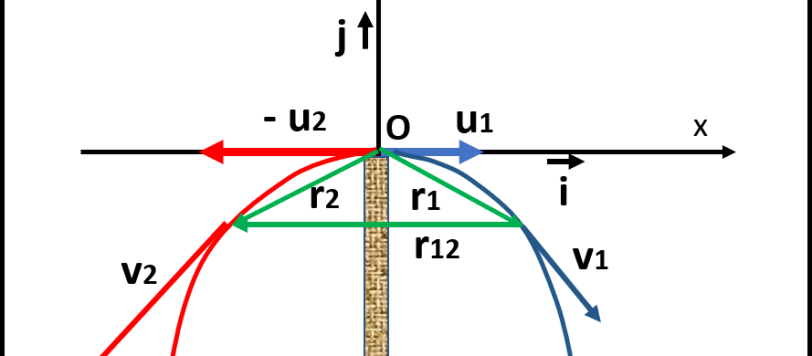
Un problema che si risolve molto elegantemente lavorando solo con i vettori (e i versori), ricordando una classica operazione tra di loro.
Lo scopo principale di questo esercizio era quello di ricavare, dalle più note formule della cinematica, la cosiddetta "formula senza tempo", ossia quella che lega la velocità raggiunta da un corpo, in funzione della velocità di partenza e dell'accelerazione a cui è sottoposta (sparisce il tempo).
Le (poche) risposte arrivate hanno fatto subito capire che diverse sono le vie di soluzione e che molto importante è la scelta dell'origine degli assi. Proponiamo tutte e tre le risposte (compresa la mia), lasciando a voi la scelta della più elegante e immediata...