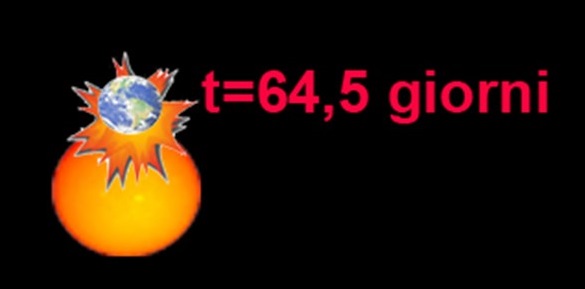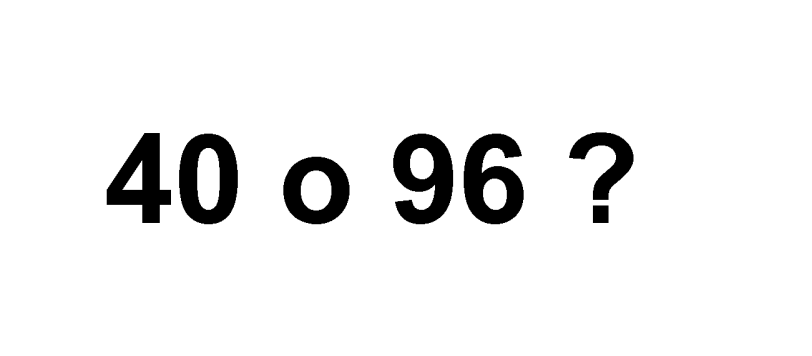In attesa di unire domanda e risposta sotto un unico articolo didattico che arricchirà l'archivio nella categoria Fisica Classica, ecco la soluzione del quiz di cinematica rettilinea, di tale semplicità che sia Arturo che Marco hanno solo dato un aiutino, sperando in qualche nuovo temerario.
La soluzione è probabilmente più facile di quello che poteva sembrare a prima vista. Maurizio è riuscito ad arrivare al dunque (dovrebbe passare un mesetto a casa dei pappidi che ama veramente tanto). Tuttavia, io presento un’altra soluzione (ben poco diversa) che fa uso di un teorema di Euclide tra quelli meno noti…
Descriviamo a cosa va incontro il nostro Giacomino. Su consiglio dell'inesauribile Maurizio abbiamo anche valutato l'ipotesi di una scala costruita e fissata sulla Luna. Ovviamente, abbiamo avuto bisogno dell'aiuto dei Papallicoli... In questo modo, abbiamo perfettamente simulato le due piante di fagiolo del racconto originario...
Approfitto della soluzione del quiz di Capodanno per un brutale assaggio della materia (non dei cibi festivi!) e delle interazioni fondamentali. Cosa c’è di meglio della celebre frase di Feynman per il titolo? Su suggerimento di Paolo (il papallicolo) penso proprio che faremo uscire, tra non molto, un articolo ben più corposo e accurato sulle interazioni fondamentali…
Questo articolo riguarda una fantastica missione della NASA che partirà tra pochi giorni (non prima del 6 agosto, comunque) e andrà letteralmente a sfiorare il Sole, penetrando all’interno della corona, dove la temperatura supera il milione di Kelvin. In altre parole, l’articolo è anche la risposta al quiz sulla missione aliena, leggermente più rischiosa…
Abbasso il capo di fronte a programmazioni e distribuzioni varie e mi limito a fare qualche piccolo ragionamento...
La soluzione del quiz sulla catastrofe terrestre, ha innescato una trattazione ben più articolata del previsto. Su suggerimento dell'onnipresente e onniveggente Daniela, si è convenuto di associare questo articolo a quello più vecchio sul blocco della rotazione di Papalla. Il titolo unico è diventato: Fermate il mondo, voglio scendere... L'articolo è stato scritto a quattro mani e cinque teste, dato che, anche se non compare tra gli autori, la supervisione di Umberto è stata essenziale.
Risolto il piccolo inghippo sull’ombra mattutina e serotina (oltre il circolo polare), il tutto si risolve con poche relazioni tra angoli o ricordando i sistemi di coordinate celesti
Nei commenti potete trovare la soluzione espressa in modi anche diversi tra loro. Noi ci limitiamo a quella -forse- più semplice che necessita delle minime conoscenze dello studio di una funzione.
Mi riferisco in particolare al quiz “appendice di whatsapp”, che ha posto un problema di fondo che riguarda la maggior parte di questi problemini che invadono il web e che spesso fanno parte dei test attitudinali e dei concorsi pubblici. Esiste una vera soluzione? E che tipo di soluzione si cerca?
Ottimo risultato ottenuto dalle nostre “punte” di diamante, abili di mente, ma anche di mano. Forse non lo sanno, ma hanno risolto il problema di un genio islamico dal nome (originale) impronunciabile…
In questo articolo descriviamo più accuratamente il metodo di esaustione e ci dedichiamo a seguire passo passo l’approssimazione del pi greco trovata da Archimede. Una trattazione a livello di scuola media, ma utilissima anche per chi voglia capire veramente come si può arrivare a conclusioni geniali senza algebra e senza trigonometria. Un’immersione completa nella mente del grande siracusano. Riportiamo anche la soluzione della quadratura del cerchio per mezzo della cicloide e un piccolo quiz.
Riportiamo la soluzione, già largamente compresa da alcuni lettori, e spieghiamo perché solo uno dei tre amici è riuscito a risolverlo. Non poteva che essere Pappo, dato che tutto si collega al suo teorema… Il quiz è solo un inizio che ci porterà verso la geometria proiettiva e la sua fondamentale importanza nella storia dell’arte.
Peppa non ha problemi a risolvere l'enigma del matematico. Tuttavia, l'ultima informazione sulla Nutella è fondamentale. Dimostriamo il perchè...
Diamo le risposte alle varie domande della seconda parte del quiz sul monte cono di Papalla, trascurando la parte relativa all'ellisse, sulla quale c'è chi sta lavorando duro e pubblicherà a breve una dettagliata trattazione. Questa parte segue pari pari quanto riportato nei commenti da Fabrìizio, con pochissime variazioni.
Nella prima parte del quasi-quiz sul Monte Cono di Papalla, volevamo solo mettere l’accento su quali siano le geodetiche di una superficie conica. Pur essendo estremamente semplici da identificare, possono creare una qualche confusione passando all’atto pratico. Chiariamo bene la loro struttura (rispondendo al quiz) e passiamo a qualche calcolo di minima difficoltà, ma di indubbio interesse.