Non pensavo risultasse così difficile. In fondo è solo una catena di eventi che si annullano di volta in volta, come nel domino.


Non pensavo risultasse così difficile. In fondo è solo una catena di eventi che si annullano di volta in volta, come nel domino.

Troppa fatica per un quiz banalissimo, in cui i numeri hanno un valore decisivo! Come già detto nei commenti, provare per trovare...
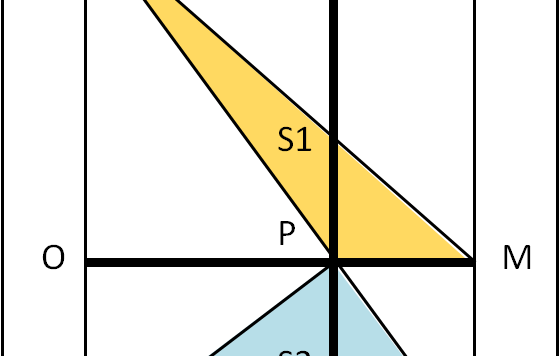
Bastava un pizzico di ragionamento e la soluzione poteva essere trovata praticamente "a mente"...
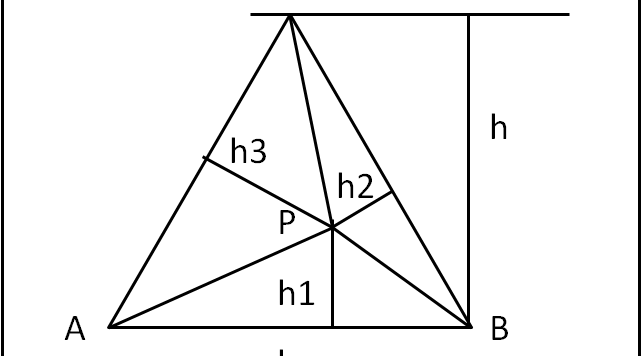
Un banalissimo e ovvio teorema (teorema di Viviani) permette di calcolare velocemente, solo per via geometrica, la probabilità richiesta.

Un esercizio che poteva, come sempre, essere risolto in vari modi. Mi compiaccio con Giorgio, Andy, Giorgio, Leandro e Maurizio. Io ho voluto aggiungere un pizzico di trigonometria...
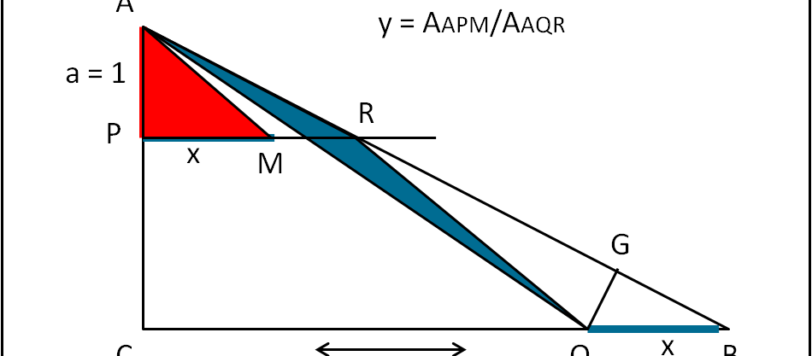
Ernesto (oltre che Andy, ovviamente) hanno risolto il quiz. Tuttavia, benché risolto in modo molto semplice si può ancora velocizzarlo. Basta ricordare che l'area di un triangolo è uguale a 1/2 del prodotto di un qualsiasi lato per la relativa altezza.
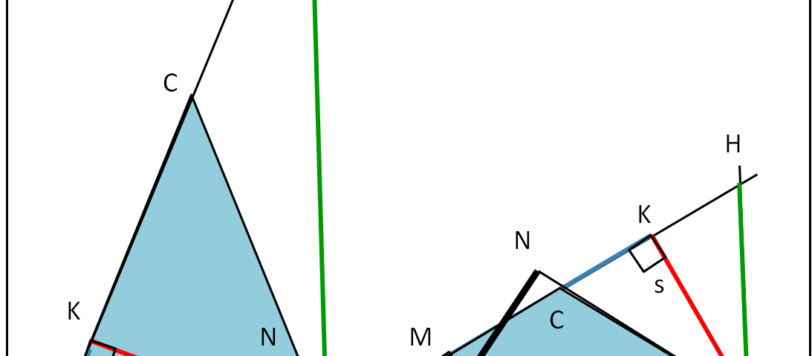
Bravi Andy, Arturo e Leandro che hanno risolto il problema, mentre noi abbiamo imparato una nuova proprietà del triangolo isoscele.
Bravi (ma non c'è da stupirsi!) Leandro e Fabrizio. Chissà che, prima o poi, qualcun' altro non voglia cercare di imitarli ?

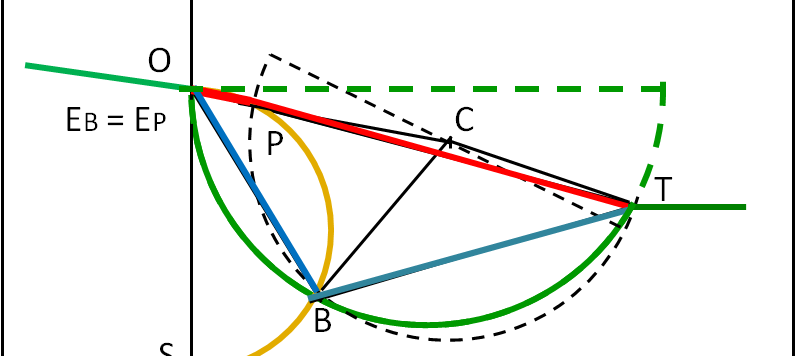
Il test di Wason: un risultato sorprendente, discusso a lungo. Noi, intanto, aspettiamo....
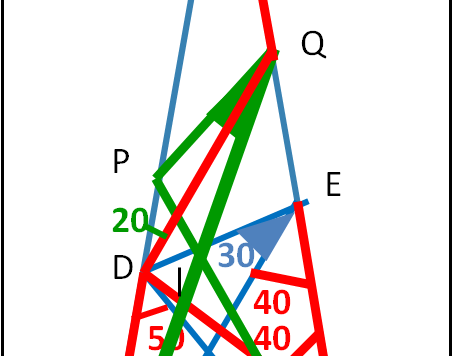
Le soluzioni di Maurizio e Andy sono ovviamente giuste (magari completatele...), ma fanno uso dei criteri di similitudine, concetto che non avevo previsto nel testo del quiz. In questo articolo trovate, invece, la soluzione di un quiz estremamente simile, sempre relativo al triangolo 80-80-20, ottenuta senza usare similitudini. Questa soluzione facilmente aiuta ad ottenere anche la soluzione al quiz originario. Volete provare ad aiutarmi?
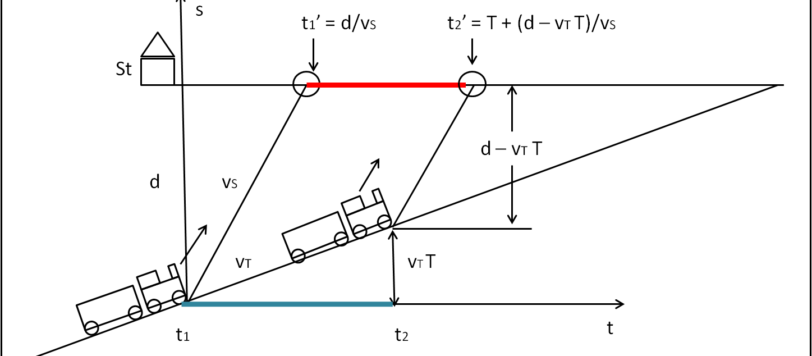
Pensavo fosse più semplice di quanto dimostratosi. I miei ringraziamenti, comunque, vanno a Michele e Mau per averci provato! Il quiz diventa un utile ripasso del piano inclinato...