Quest'articolo tenta una dimostrazione geometrica unitaria della complanarità e non complanarità delle facce di solidi semplice come il tetraedro e la piramide. Lo fa attraverso le proiezioni e devo dire che la visione delle varie figure non è proprio banale, da cui i tre asterischi.
Innanzitutto, un bravo particolare a Leandro che in qualche modo (magari non il più semplice) è riuscito ad allacciare la scarpa... D'altra parte nel poco conosciuto metodo per il calcolo dell'area di un triangolo (e di un poligono qualsiasi) c'è la mano di Gauss. In realtà il metodo "laccio da scarpa" prende anche il nome […]
Un quiz che ha ottenuto poco successo, ma che ha visto la risposta qualitativamente esatta di Daniela. Direi che vale la pena, comunque, di darne anche il risultato quantitativo.
Come previsto, noi non siamo certo milioni, ma malgrado le ferie abbiamo superato il limite... Un quiz nato a fine ottocento che ha visto la partecipazione di milioni e milioni di appassionati. Oggi, temo che il numero delle risposte esatte diminuirebbero di molto, tranne che da noi...
Sfatiamo, in qualche modo, una leggenda sui buchi bianchi che vengono, quasi sempre, identificati come buchi neri "al contrario", ossia come oggetti da cui esce di tutto e niente può entrarvi.
Una soluzione forse inaspettata, ma , in fondo, bastano due procedure per avere la sicurezza. Un po' più di fantasia è necessaria per risolvere un caso apparentemente impossibile.
Un semplice problemino di meccanica o, meglio, di riflessione che si trasforma facilmente in una regola matematica altrettanto semplice.
Bravo Agapito, anche se avrebbe dovuto essere un quiz molto facile.. Ma nelle superiori sembra un ostacolo molto grande...
Poca voglia o tempo per affrontare questo quiz? O -magari- più difficile del previsto? Comunque sia, riporto la soluzione piuttosto rapida direi. Chi vuole continuare a provare, eviti di leggere...
Per risolvere questo quiz, non veramente proibitivo, è necessario farsi uno schema accurato e completo di tutte le configurazioni possibili e, poi, eliminarne un po' alla volta, fino a che garantiscano una risposta esatta. Ovviamente, Fabry e Paolino lo hanno risolto brillantemente.
Bravissimi i nostri Enrico, Alex, Silvano e Paolo! Anche se in modi leggermente diversi hanno risolto brillantemente il quiz. Che siano tutti abili giocatori di pingpong?
Riporto la soluzione anche se il quiz può sempre essere affrontato da chi vuole provare col puro ragionamento. Luigis è stato molto bravo; Paolo è stato bravo a provare... "no comment" per Frank che ha cercato una soluzione da golfista per un problema in cui la fortuna non doveva entrare in gioco..
Come annunciato, il problema necessitava di una preparazione al livello delle medie superiori. L'importante era scegliere bene gli assi cartesiani di riferimento e avere un po' di intuito. Come sempre, Fabrizio è riuscito a far sì che i tre fratelli ottenessero il massimo dal terreno avuto in eredità. Inoltre, ha impreziosito la soluzione con una bella animazione molto istruttiva.
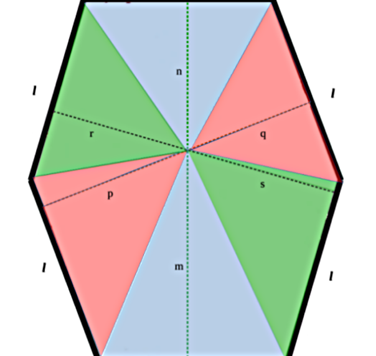
Una soluzione non certo banale. Nella sua descrizione ho creato una pausa, dove , ottenuto il risultato finale, si può ancora agire da soli per darne la spiegazione logica (quindi, una soluzione a due stadi...). Bravissimi Alex e Fabry e molto vicino al risultato esatto anche Paolo.
La soluzione del quiz che ho seguito io, vede la morte del tesoriere, la sopravvivenza (almeno momentanea) del medico e una brutta fine per il re... Vediamo come si sono svolti i fatti. Il tesoriere sa di non essere in grado di poter preparare un veleno più potente di quello del medico. Decide allora, di […]
Concludiamo il quiz dei fiorini, riportando la soluzione migliore.