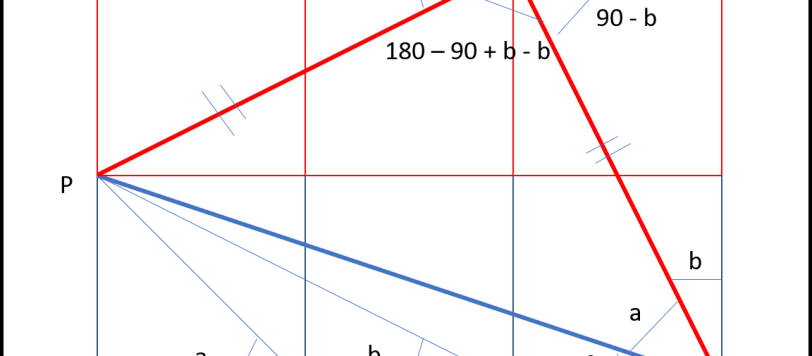
Ho aspettato a lungo prima di dare la soluzione al quiz su Gigi Riva, per rispetto alla passione e volontà mostrata da Franco. Ecco, adesso, una doppia possibilità, con o senza trigonometria. La trigonometria è quella che ha usato anche Franco per risolvere il problema. Iniziamo col rendere generale la soluzione, chiamando a la distanza […]
Nella soluzione che propongo a questo quiz ci si rifà pari pari alla formula trovata da Dirac, sia sostituendo pi greco al numero 2 sia scrivendo 2 in altro modo... Ringrazio ufficialmente Karl, Andy e Fabrizio per la volontà, l'interesse e le capacità dimostrate!
La soluzione del quiz è stata trovata da molti, in modo più o meno diverso. Alcuni hanno scelto la via meno banale, altri no. Essenzialmente vi sono due modi per risolvere la questione. Uno di carattere empirico (che avrebbe bisogno di una verifica anche se è molto intuitivo) e uno legato al calcolo combinatorio. La […]
E' piuttosto strano che a un quiz con tanti asterischi si possa rispondere con due soli asterischi. Il motivo è, però, semplice: il quiz non ha ancora una soluzione!
Nessuno ha dato una risposta... pazienza. Il vero scopo del quiz era, comunque, duplice. Innanzitutto avvicinarsi a una strategia realmente seguita da alcuni animali per la loro caccia e, poi, cercare di definire nel modo migliore un gioco da tavola basato su questa strategia. Forza, siamo appena all'inizio. I lauti guadagni saranno equamente divisi...
Ecco la soluzione del tappo multiuso. Un po' di ricordi delle proiezioni ortogonali di un solido, come ha detto Fabrizio, e il tappo si costruisce quasi da solo...
La soluzione che riporto si rifà a un celebre scienziato greco, Apollonio di Perga, famoso non solo per aver "inventato" gli epicicli, utilizzati poi da Tolomeo. A lui si deve una nuova definizione di cerchio, capace di dare al capitano inglese tutte le informazioni possibili. Alla fine trovate una preziosa aggiunta del nostro caro Maurizio che ha voluto arrivare al dunque attraverso nientepopodimeno che la geometria inversiva.
Ecco la soluzione del quiz sulle uova buttate dal grattacielo. Una soluzione volutamente molto lunga per rendere chiari i vari approcci, anche attraverso esempi concreti. Umberto ha dato, ovviamente, il risultato esatto, ma ha anche sviluppato un software che trova il risultato analizzando tutte le combinazioni, confermando il numero di lanci trovato come il minimo possibile. Lo pubblicherà nella seconda parte della soluzione
Questa è una soluzione volutamente "complicata" per rispondere al quiz "Pitagora è sempre Pitagora". Lo scopo è quello di richiamare concetti che abbiamo trattato ultimamente. Molto gradita è stata anche l'intrusione di Oreste Pautasso e del suo enunciato decisamente più "corposo".
Non bastava Erone a regalarci triangoli con i lati e le aree intere, si ci è messo anche quel genio incontrastato che è stato Eulero, prospettandoci un supermattone! Un bravissimo a Maurizio che ha risolto il quesito da par suo.
Un problema che ci avvicina al numero di Nepero (o di Eulero) "e" e che, inoltre, ci permette di richiamare lo studio di una funzione, i limiti e le derivate, nonché un po' di logaritmi naturali.
Beh... cari amici, devo dire che il nostro Oreste Pautasso ha cercato veramente di presentarci tutti i 54 metodi di risoluzione della prima parte. Abbiamo dovuto abbatterlo dall'albero su cui si era rifugiato per farlo smettere. Ovviamente, per partito preso e per alto senso democratico, nessuno dei suoi metodi può essere considerato "elegante" come quello che avevo in mente io!
E' un momento in cui la campagna SETI, dedicata a cercare di "sentire" segnali provenienti da abitanti di esopianeti, tecnologicamente avanzati, sta avendo nuovi impulsi. Che speranze abbiamo?
La soluzione è stata più laboriosa del previsto... tuttavia, ringrazio tutti coloro che hanno provato. Il numero 70 girava, ma quasi sempre con un ragionamento non coretto del tutto.
Questo quiz di logica più che di matematica è stato letteralmente "sbranato" da Maurizio e nessuno (tranne Ale) ha avuto la voglia di cimentarsi. Cercheremo, la prossima volta, di mettere il bavaglio al nostro Mau... che di questi quiz, relativamente semplici, ne fa un solo boccone!
Questo articolo è estremamente interessante e l'argomento ben poco analizzato (finora almeno). Probabilmente apre un nuovo "mondo" di studi. Leggetelo, quindi, con molta attenzione e mettetevi alla prova. Come forse avrete immaginato, il riferimento al golf non è così forte come si sarebbe potuto credere. Lo scopo era di scuotere un po' il nostro Frank sempre in lotta per scalare posizioni (e anche per prenderci un po' in giro). Che anche lui "scenda" al nostro livello, forse un po' troppo teorico per un tecnogolfista...