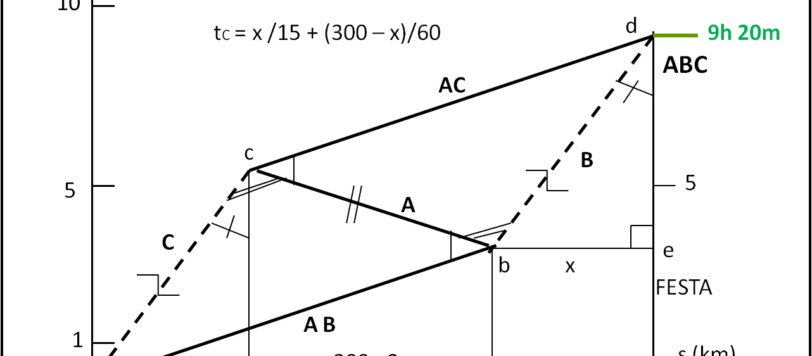
Una soluzione decisamente più semplice di quanto potesse sembrare. Basta "non perdere tempo".
Abbiamo discusso a lungo della curvatura di uno spazio a due dimensioni e abbiamo visto come la geometria che lo descrive si discosti completamente da quella euclidea che impariamo a scuola. Come detto varie volte, la curvatura di uno spazio (lasciando da parte il tempo, almeno per adesso) è legata strettamente alla relatività generale, un argomento che aspetta ancora di essere affrontato in modo diretto e decisivo. Vale la pena capire ancora meglio cosa si intende per “curvatura”
Fotografando i cieli stellati da un po' di tempo, alle volte sento il bisogno di cambiare location e trovare situazioni nuove... Fortunatamente però, delle volte sono le situazioni più strane che si presentano quasi spontaneamente ai miei occhi, come in questo caso... Una bella serata di Luna piena, solitamente snobbata da qualsiasi astrofilo, si è […]
Iniziamo, finalmente, il nostro lungo viaggio nel mondo degli integrali. Useremo due modi per definirli, per poi legarli strettamente attraverso un teorema fondamentale. Non abbiate paura, però: il discorso sarà molto semplice almeno fino alla “digestione” completa dei concetti più importanti. Riuscire, poi, a calcolare tutti gli integrali che si vorrebbero, diventa esercizio ben più arduo anche per i professionisti. Si usano vari “trucchi” e le serie ci aiutano. Ma… non corriamo. Cominciamo con qualcosa che è veramente alla portata di tutti: le aree dei rettangoli, dei triangoli e dei trapezi…
N.B.: i primi articoli sugli integrali sono comprensibili e utili a TUTTI, anche a coloro che non sono riusciti a seguire le tantissime lezioni sulla matematica. Vi invito perciò a leggerli ugualmente...
Questo è solo un preambolo estremamente riduttivo e rozzo (addirittura non del tutto esatto). Serve solo per farsi la bocca in attesa di quanto promesso a Dany e ad Alvy. Tutto gira intorno al quinto postulato di Euclide, quello delle rette parallele. Ma per discuterne a fondo e per applicarlo alla fisica dell’Universo è necessario fare un lungo percorso storico e matematico. Fin dall’inizio, però, capirete bene perché il nostro “circolo” (e il libro precedente) si chiama Infinito TEATRO del Cosmo.
Questo articolo ci mostra, qualitativamente, come la relatività generale implichi una curvatura dello spaziotempo e non solo dello spazio. Purtroppo, noi intuiamo abbastanza bene solo la seconda. Limitandosi ad essa la relatività sarebbe un’assurdità. Non ci sono formule, ma il concetto non è banalissimo, benché fondamentale per immergersi veramente nella problematica dei buchi neri e non solo. Non fatevi ingannare dall’apparente banalità: se capite l’essenza del concetto di base, tutto sarà più facile.
Una specie di racconto assurdo… ma non troppo, forse…