Oggi, 23 novembre, è la giornata mondiale dedicata a Fibonacci e ci uniamo alle celebrazioni riproponendo la tesina che la nostra Valentina scrisse nel 2018 per il suo esame di maturità.
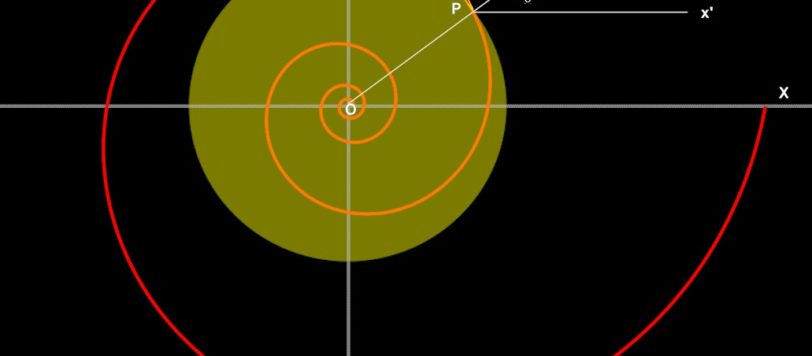
Data l'equazione polare della spirale logaritmica, non è difficile passare alla corrispondente rappresentazione parametrica. Meno immediato è il cammino inverso: da parametrica a polare. Ma percorrendo questo sentiero si può meglio comprendere il significato geometrico dei parametri che stabiliscono la forma della curva.
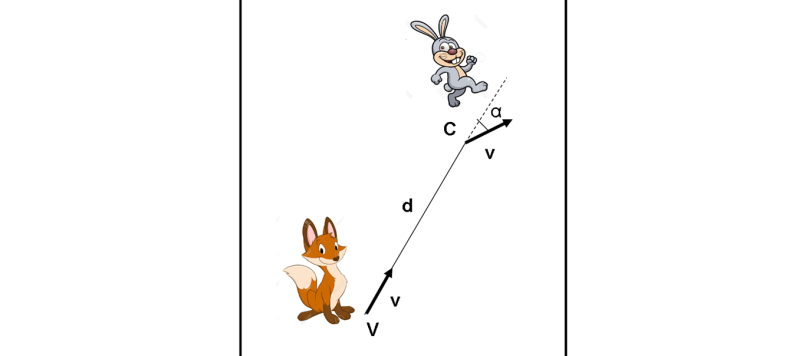
Un simpatico esercizio di cinematica, che ci porta velocemente nel mondo delle spirali che tanta importanza hanno per l'Universo. Noi ci limitiamo, per il momento, a una volpe e a un coniglio...
Spesso è sorprendente come certi concetti matematici apparentemente astratti abbiano così tante manifestazioni nel mondo reale! Tra i più sorprendenti c'è senz'altro il numero aureo, al quale ho dedicato la tesina del mio esame di maturità, concentrandomi sulle applicazioni in campo artistico, dopo averne spiegato a grandi linee le caratteristiche matematiche e geometriche.
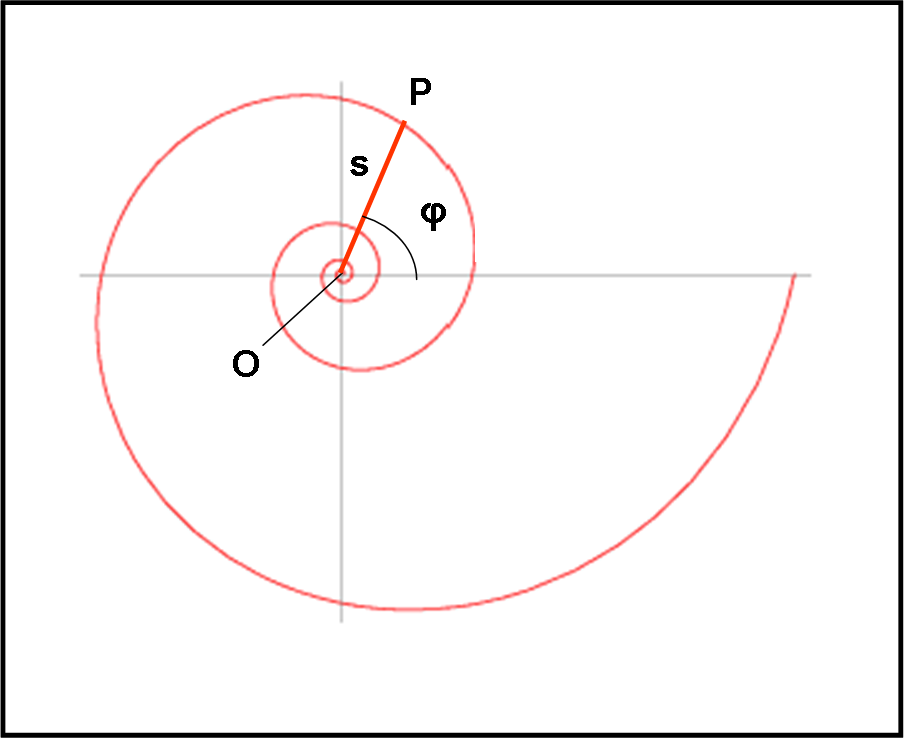
L’uso della funzione esponenziale, in particolare di quella che si basa sul numero e, permette di descrivere la celebre spirale logaritmica. Essa rappresenta un passo in più rispetto a quella di Archimede, anche se è altrettanto semplice ed è la curva più utilizzata nel Cosmo, a tutti i livelli di grandezza. Oltretutto, ha anche influenzato le proporzioni armoniose dei monumenti, delle statue e delle pitture, a partire dai capolavori greci (rettangolo aureo). Ovviamente, ha a che fare con i numeri di Fibonacci.