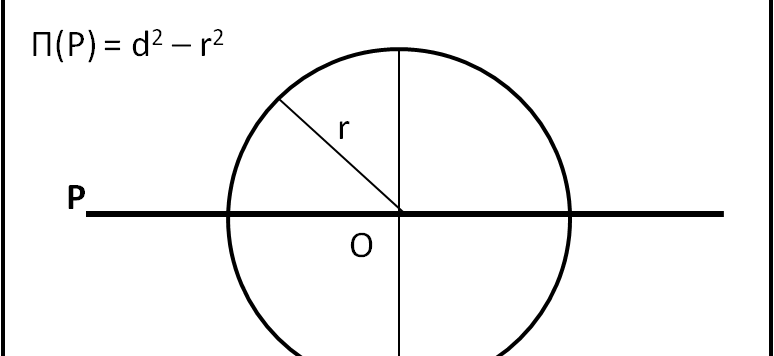
Il più grande geometra di tutti i tempi dimostra che anche i punti hanno una loro "potenza".
Risolto (da Leandro) il problema della costruzione della tangente all'ellisse in un punto, possiamo cominciare a giocare a biliardo su un tavolo dalla forma molto particolare: l'ellisse.
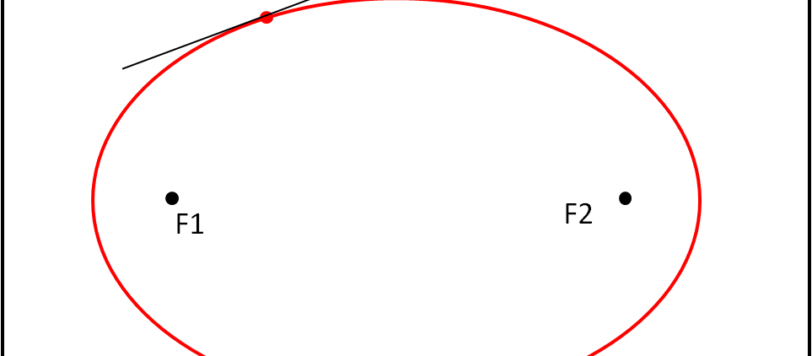
Prima di giocare con un biliardo un po' speciale, fatemi fare una domanda-quiz sicuramente non difficile.
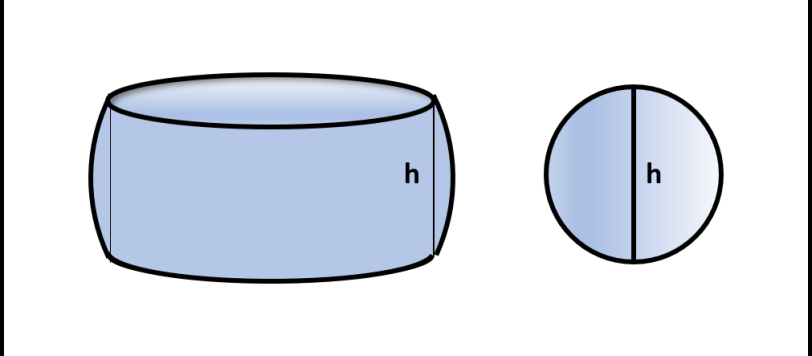
In questo ultimo articolo riguardo a Mamikon risolviamo, con il solo "calcolo visuale" , il problema relativo alla talpa spaziale. Possiamo dire di avere introdotto il teorema di Mamikon ... tridimensionale!
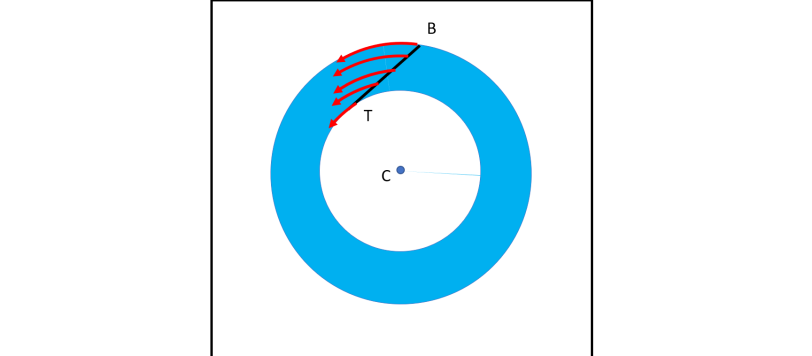
Questo articolo non riporta solo la soluzione al primo di due recenti quiz, ma vuole descrivere molto di più e, quindi, non perdetevelo! La geometria può diventare una specie di romanzo d'avventura... Potremmo chiamarla "geometria dinamica"!
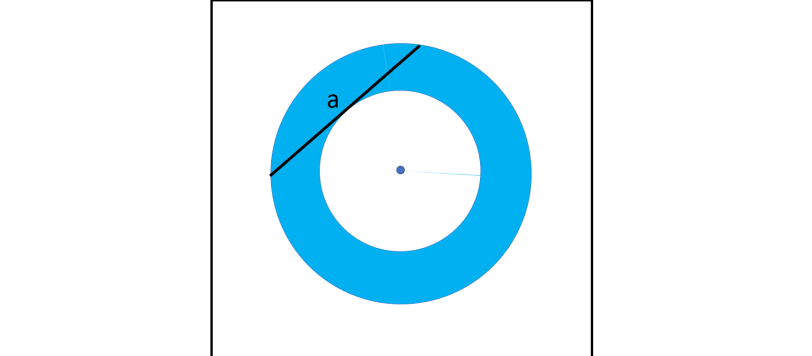
Un quiz dall'apparenza banale e facilmente risolvibile ha portato a un teorema che nemmeno i greci avevano formulato. Potete fermarvi al livello che volete.
In questo articolo cerchiamo di soffermarci un attimo su casi particolari di cubiche, in modo da osservare come si possano avere sia flessi orizzontali che obliqui sia massimi e minimi (ma non sempre). Usiamo solo lettere per affrontare i casi particolari in modo generalizzato. In questo modo, il linguaggio matematico diventa un linguaggio a tutti gli effetti e permette da solo di descrivere il tipo di risultato ottenibile nei vari casi. Un esercizio che reputo fondamentale per diventare sempre più amici delle lettere e non solo dei numeri... Seguite i passaggi con molta calma, riflettete a lungo ed eseguite tutti i disegni che volete...
Vi chiedo perdono per due motivi. Innanzitutto, perché il problema fisico (ma anche matematico) è di estrema semplicità. Inoltre, perché ho scritto un articolo di risposta assurdamente lungo per ciò che si chiedeva. Spero, però, che serva a fare un bel ripasso di derivate e limiti…
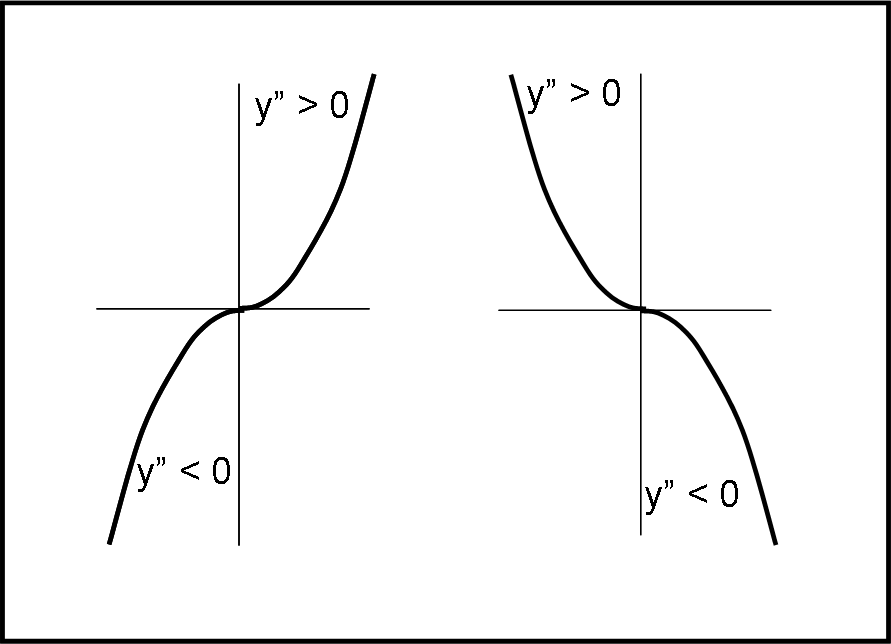
Dopo aver introdotto i massimi, i minimi e i flessi orizzontali in modo molto preliminare, è giunta l’ora di affrontarli più accuratamente attraverso le derivate successive di una funzione. Ci arriveremo lentamente in modo da comprenderne appieno il significato sia matematico che geometrico.
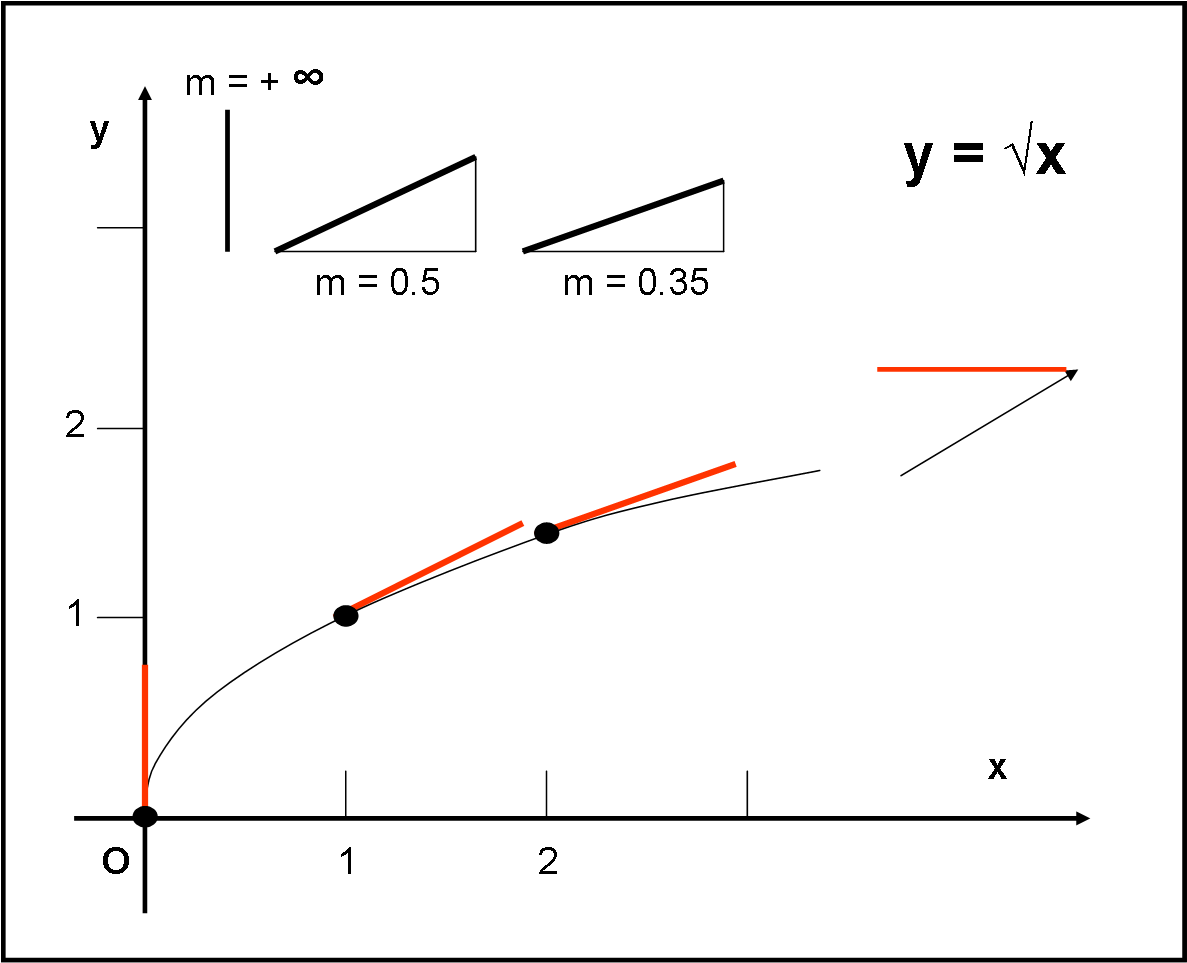
Cominciamo a calcolare alcune derivate di funzioni particolari, rappresentate dai semplici monomi. Una rapida analisi dei risultati ci insegna che esiste una facile regola generale che evita il noioso passaggio attraverso il rapporto incrementale. Segue un’appendice per i più … volenterosi.
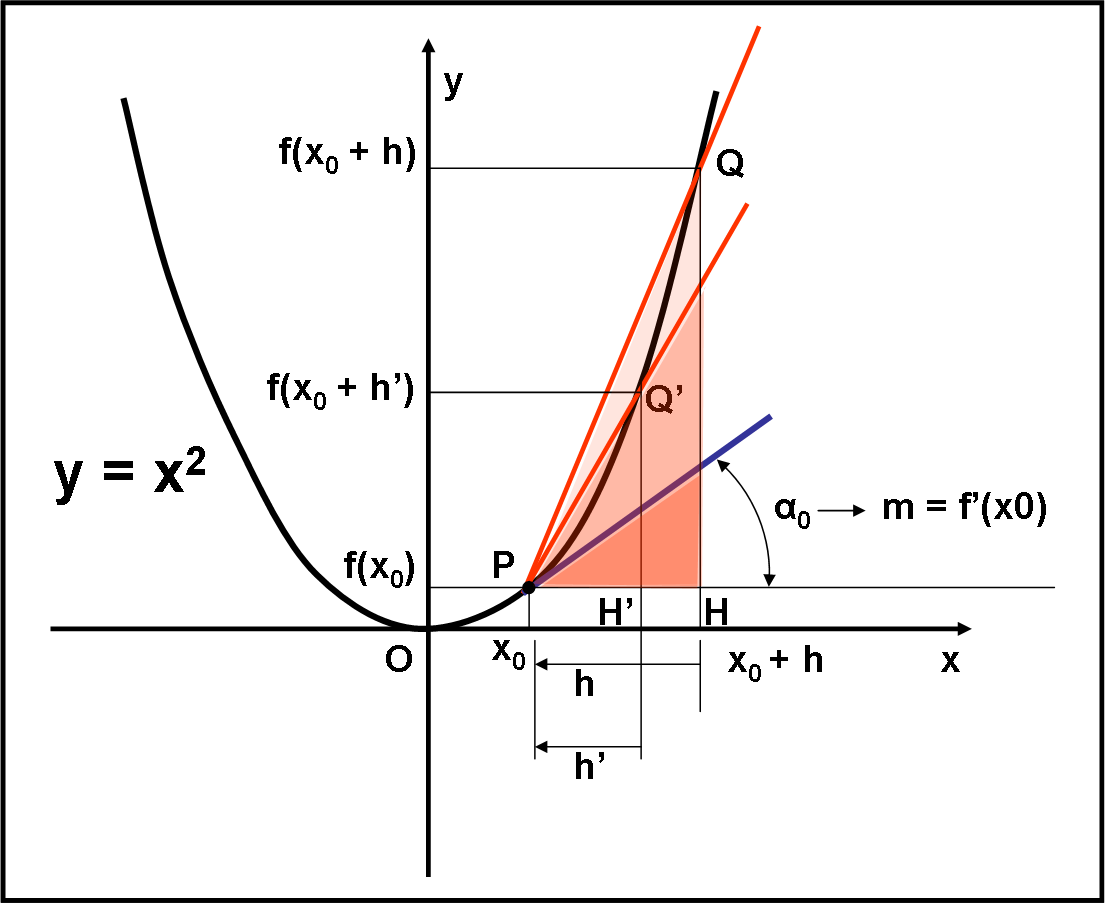
In questa parte, veramente fondamentale, calcoliamo la prima derivata di una funzione che non sia una retta e ne diamo il significato geometrico. Lo scenario si amplia sempre di più.
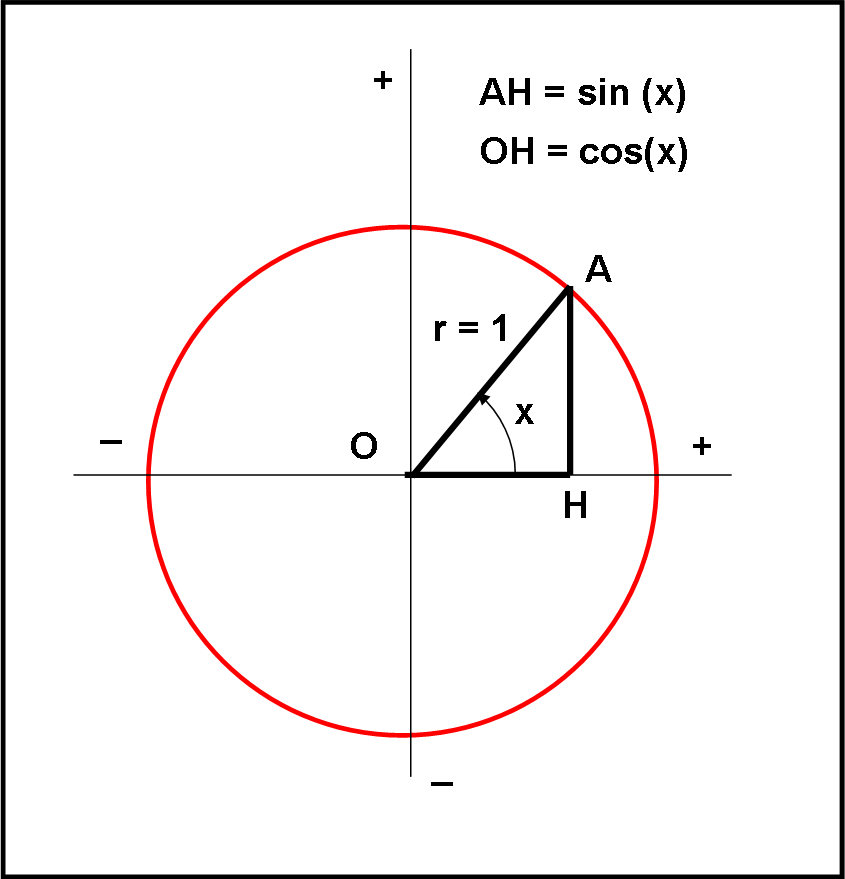
Abbiamo già parlato delle più semplici funzioni trigonometriche. Sia perché ci sono servite per definire il coefficiente angolare di una retta, sia perché attraverso di loro si può passare da un sistema di coordinate cartesiane a uno di coordinate polari (e viceversa). L’uso delle funzioni trigonometriche permette, in genere, di calcolare facilmente le componenti di un segmento qualsiasi rispetto ai due assi cartesiani. E mille cose ancora… Tuttavia, restano comunque delle funzioni ed è giusto studiarle come abbiamo fatto per le coniche, le rette, il logaritmo e cose del genere.
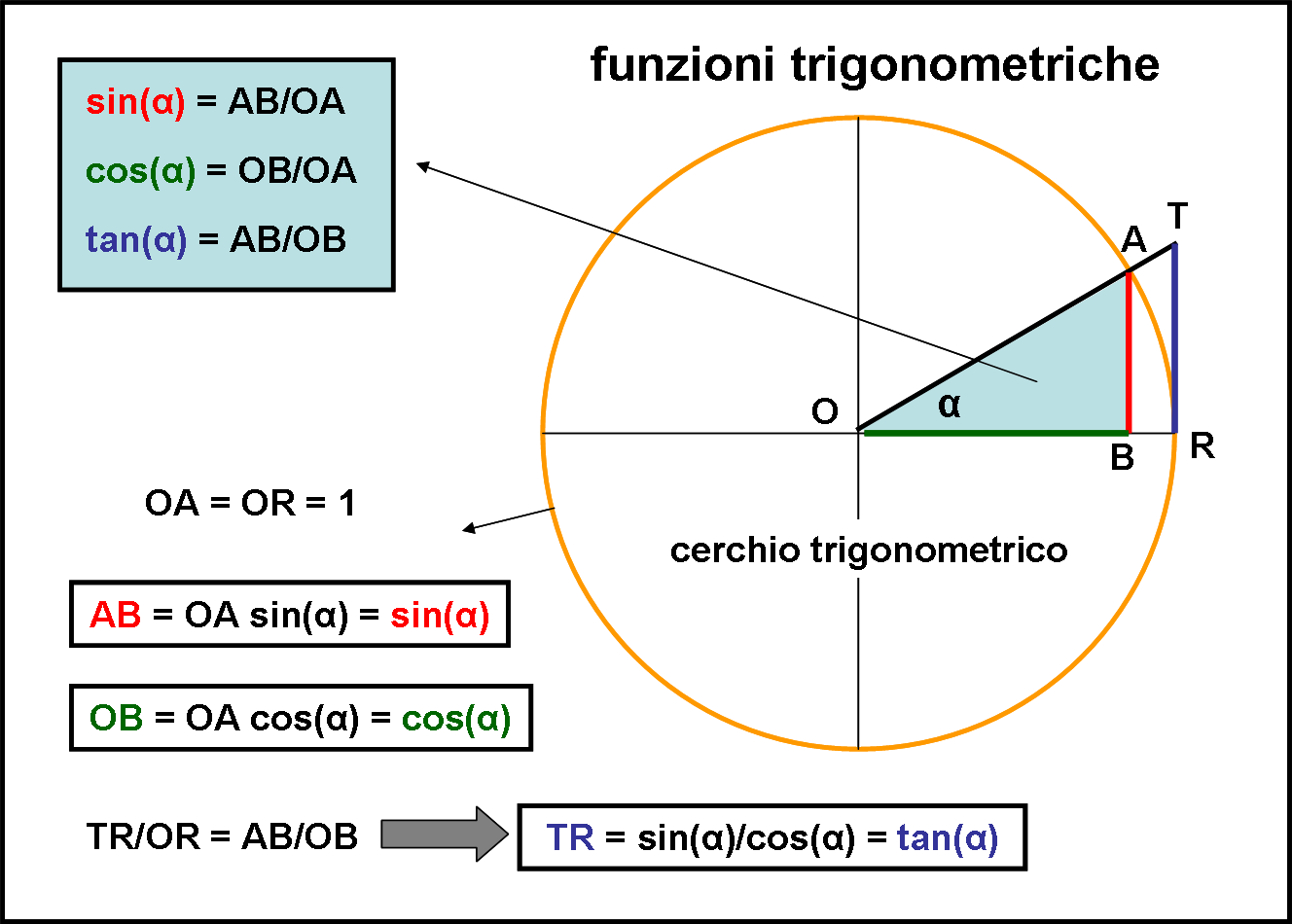
Qualcuna/o dirà: “No… aiuto! La trigonometria no… non l’ho mai digerita!”. Mi spiace per lei/lui, ma non possiamo farne a meno. E poi perché tanta paura? Anche lei nasce molto facilmente dal celebre triangolo rettangolo tanto caro a Pitagora e permette di capire il significato più profondo di certi numeri che sembrano essere solo numeri, ma che sono, invece, qualcosa di ben più importante. Chiedetelo alla cinematica, alla dinamica e a tutta la fisica…