Disegniamo un 'ellisse richiamando Leonardo.
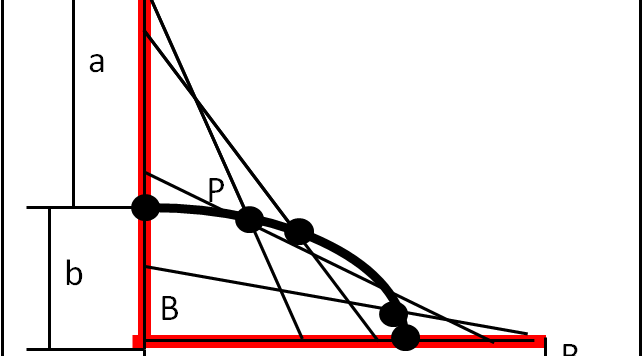
Il teorema di Pitagora è sicuramente il più dimostrato in assoluto. Tra i tanti metodi vediamo come si destreggia un ... mulino ad acqua.
Due studentesse liceali (dal colore scuro della pelle, ma dal cervello decisamente chiaro e limpido) hanno risolto un problema su cui hanno lavorato per secoli i grandi matematici. Abbiamo di fronte una vera opera d'arte matematica!
Soluzione del quiz "il fratello sfortunato di pitagora" ovvero il teorema di Arogatip
Una lezione di semplicità e genialità di un grande ingegnere greco
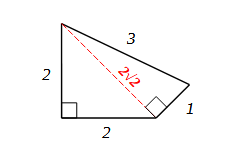
Questo articolo nasce come una serie di considerazioni e prove numeriche “sul campo” relative al teorema di Pitagora e all’ipotesi di Enzo su di una sua estensione a qualsiasi poligono, che ha ottenuto un primo riscontro particolare grazie alla “riscoperta” della spirale di Teodoro di Cirene. L’ipotesi di Enzo era quella di vedere, se possibile, l’applicabilità del teorema di Pitagora anche a poligoni con più di tre lati. Così ho deciso di tentare algebricamente se fosse stato possibile trovare una identità di tipo pitagorico (inizialmente limitata solo per valori interi) per poligoni generici con più di tre lati.
Un racconto geometrico molto personale che ha mostrato la mia... ignoranza!
Non vi spaventi il titolo... basta pensarci un po' e salta all'occhio che non è altro che il nome Pitagora al contrario.
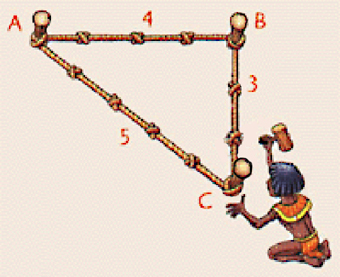
La geometria "applicata" delle prime civiltà ci stupisce sempre di più. Probabilmente, la geometria nasce addirittura prima del linguaggio, come si può evincere anche dalla disposizione di molte strutture megalitiche.
A cosa si riferiscono le due date del titolo? Al teorema di Pitagora e in particolare a due "nuovi" metodi usati per dimostrarlo.
Partendo dal teorema di Pitagora sul piano arriviamo a quello su uno spazio curvo, grazie al tensore metrico... le cose si complicano e le sommatorie si affollano.
Questa è una soluzione volutamente "complicata" per rispondere al quiz "Pitagora è sempre Pitagora". Lo scopo è quello di richiamare concetti che abbiamo trattato ultimamente. Molto gradita è stata anche l'intrusione di Oreste Pautasso e del suo enunciato decisamente più "corposo".
Un quiz veramente semplice, che lascerei ai principianti... (però rispondete!).
La geometria, anche quella più semplice, può diventare un vero spettacolo. Soprattutto se c'è di mezzo Tolomeo, grandissimo scienziato, troppo spesso associato solo alla sua visione eliocentrica dell'Universo.
Pappo di Alessandria (IV sec. d.C.) è stato sicuramente il massimo matematico del periodo ellenistico e alcuni suoi teoremi sono considerati la base per gli studi più moderni di geometria proiettiva. Tra le tante cose fatte, Pappo è riuscito a generalizzare il teorema di Pitagora, rendendolo solo un caso molto particolare. Vi propongo il problema […]
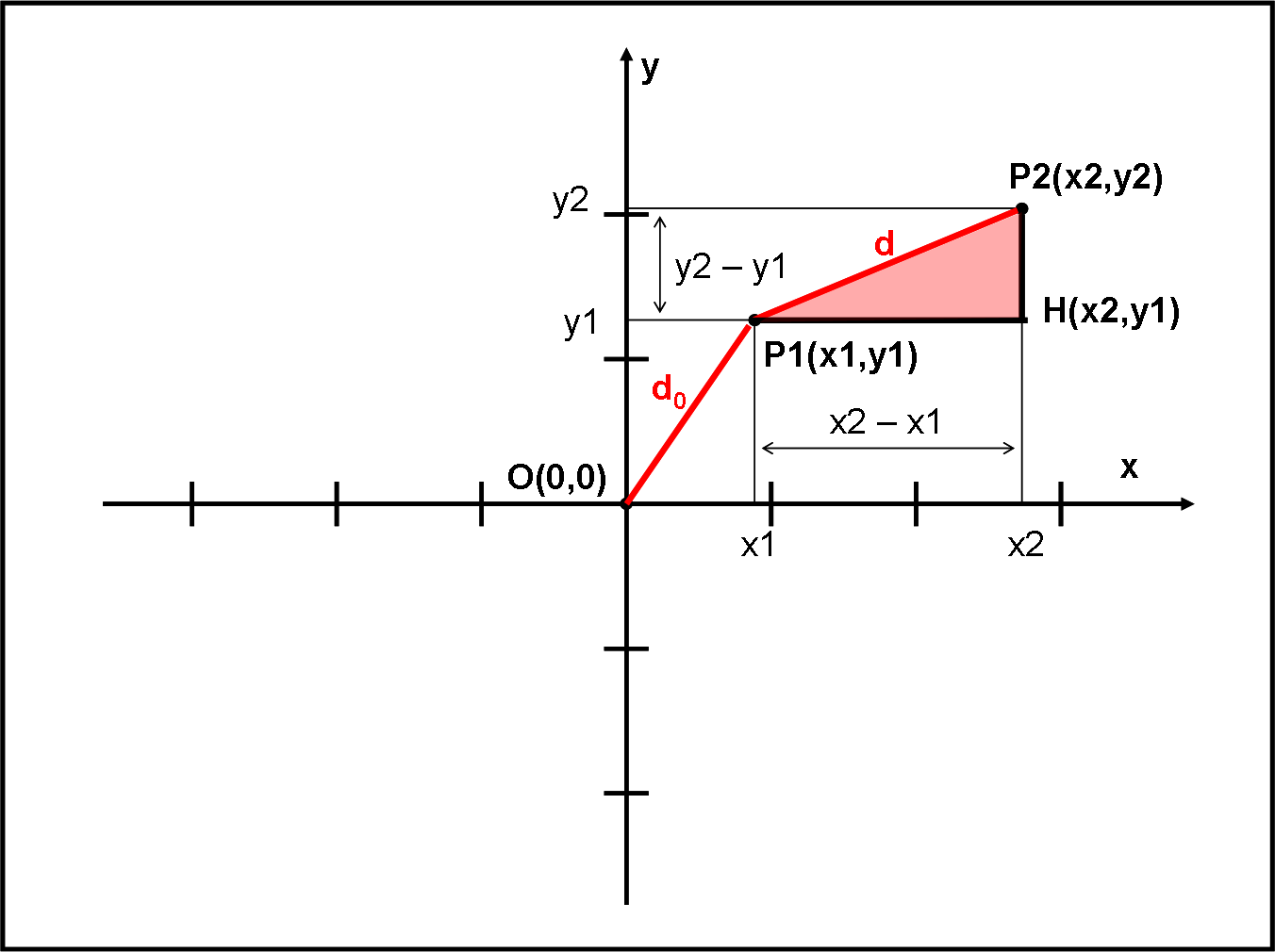
Ci siamo costruiti un sistema di riferimento semplice e utilissimo. Vedremo subito come utilizzarlo. Prima inseriremo nuove stazioni un po’ dappertutto e, chiamandole con le loro coordinate, sapremo trovarle immediatamente. Poi inizieremo a costruire monorotaie sempre più complicate. La matematica diventerà l’unico linguaggio in grado di aiutarci nella loro “sistemazione” nella rete ferroviaria, ossia nel piano del foglio.