Quanto è lungo un rotolo di carta igienica?


Nella serie "MATEMATIZZIAMO IL NASTRO DI MÖBIUS", abbiamo visto come generare delle varietà bidimensionali in modo astratto. Riprendiamo in modo meno formale tale procedimento,estendendolo allo studio delle tri-varietà,ossia le varietà di dimensione tre,che non sono rappresentabili nello spazio tridimensionale.

Nato nel 1854, Poincaré fu l’ultimo genio mondiale di cognizioni scientifiche universali, non frenato da alcuna barriera disciplinare, forte d’una erudizione scientifica portentosa. Formulò quello che è stato il il quinto problema del Millennio, la congettura che porta il suo nome. Per non parlare del grosso contributo dato allo studio della relatività ristretta.
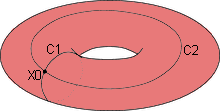
Eccoci dunque alla prima puntata della serie dedicata alla congettura di Poincaré. Per capire bene l'enunciato della congettura è necessario conoscere il concetto di "semplice connessione". Procederemo in modo intuitivo, aiutandoci con disegni e ragionamenti abbastanza pratici. Non tutti gli enunciati saranno dimostrati formalmente. D'altro canto, quanto fatto nella prima serie topologica dovrebbe essere sufficiente per comprendere a fondo questo articolo.

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica Con l'articolo sul piano proiettivo si conclude la serie "Matematizziamo il nastro di Mobius" in cui sono stati esposti i concetti fondamentali della topologia generale. Ma lo topologia non finisce qui.Il tutto andrà poi esteso alle tri-varietà; fino ad ora ci siamo occupati di […]
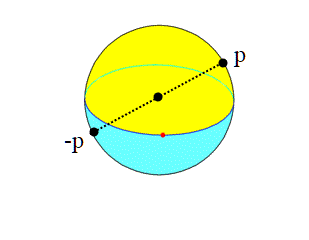
In questo articolo scoprirete che il piano proiettivo è tutt'altro che un piano. Analizzeremo vari modelli di questa superficie topologica che risulta ancora più complicata della bottiglia di Klein, pur avendo con essa delle affinità.

Continua il nostra viaggio nell'affascinante mondo delle superfici ottenute con il passaggio al quoziente. Riusciremo a costruire una superficie chiusa e non orientabile, la superficie di Klein. Ma a differenza di quelle viste fino ad ora,questa superficie non esiste nello spazio tridimensionale.
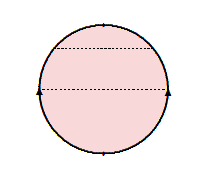
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica Ci sono più modi per costruire una sfera con la topologia quoziente. Il più semplice consiste però nel fare il quoziente di un disco. Fino adesso abbiamo fatto quozienti di quadrati e rettangoli, ma nulla ci vieta di farlo di altri sottospazi topologici. Consideriamo […]
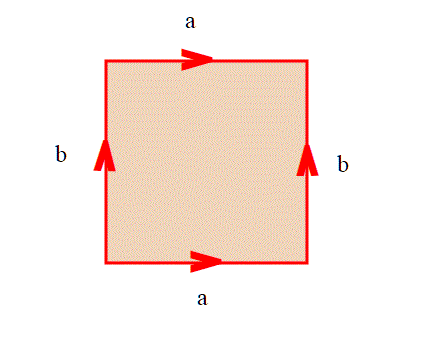
Un punto d'incontro fra il toro descritto da Arturo negli articoli sulla geometria dello spazio, e il toro "topologico" ovvero descritto in modo astratto tramite la topologia quoziente. Dimostreremo in questo articolo che le due superfici sono omeomorfe.

Affrontiamo oggi i primi due esempi di superfici topologiche generate partendo dal quoziente di uno spazio topologico basilare (un quadrato o un rettangolo) . Partiamo dalle superfici più semplici da generare: il cilindro e il nastro. Fra le altre cose vedremo anche immediatamente la differenza fra superfici orientabili e non orientabili, e la definizione di orientabilità.
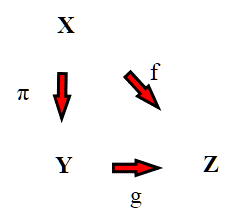
Volevo fare un esempio semplice per applicare gli ultimi risultati (più uno inserito al volo) alla costruzione di un omeomorfismo fra uno spazio quoziente ed un sottospazio definito da una espressione analitica. Questo ci darà un metodo generale per studiare le superfici quoziente e rapportarle a quelle dello spazio Euclideo,
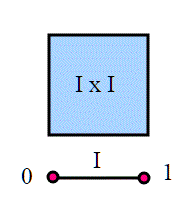
Un articolo al di fuori della serie topologica, ma necessario per continuare le nostre costruzioni sul quoziente topologico. Vedremo come dimostrare che l'intervallo chiuso in R è uno spazio compatto. In realtà , la dimostrazione riguarda più l'analisi matematica che la topologia.

Lo scopo di questo articolo è quello di chiarire per bene cosa sono gli spazi quoziente, e come siano collegati ad altri spazi che conosciamo molto bene. Il collegamento è realizzato tramite il concetto più importante della topologia: l'omeomorfismo. Questo teorema diventa necessario per realizzare degli omeomorfismi fra spazi topologici derivanti da una operazione di incollatura, ovvero di passaggio al quoziente.
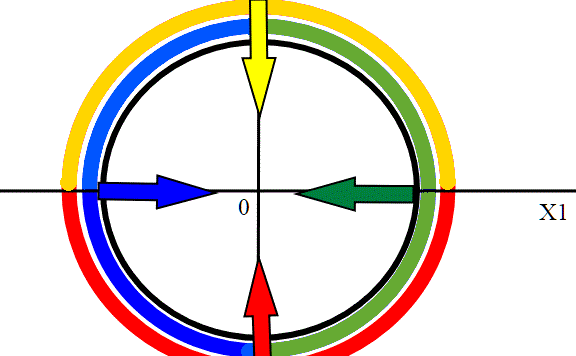
Non è proprio banale costruire un atlante per una varietà topologica. Per cui voglio fare un esempio "pratico", usando una varietà unidimensionale; Il cerchio è infatti una varietà topologica di dimensione 1.La scelta ovviamente è per comodità grafica e di notazioni.
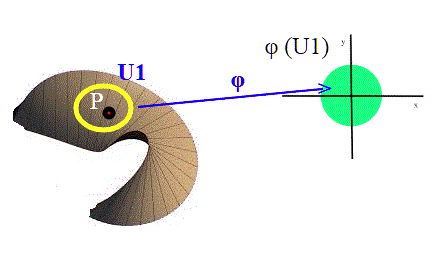
In questo articolo dobbiamo sforzarci per capire bene la differenza fra "locale" e "globale"; una superficie, o più in generale. una varietà topologica, è localmente simile ad uno spazio euclideo, ma quasi sempre non lo è globalmente. Il concetto di simiglianza viene tradotto molto bene dagli omeomorfismi.

Grazie alla topologia quoziente saremo in grado di costruire degli spazi topologici nuovi e molto interessanti, tipo appunto il nastro di Möbius. Si, siamo arrivati al dunque, ma ancora un attimo di pazienza. Le costruzioni che faremo ci faranno capire l'importanza in matematica delle relazioni di equivalenza, con le quali è possibile perfino "incollare" dei punti di uno spazio topologico.