Ho lasciato passare un po' di tempo prima di andare avanti con la Topologia. E' ora di concludere con i concetti iniziali, ed affrontare nozioni più avanzate che ci porteranno alla matematizzazione del nastro.
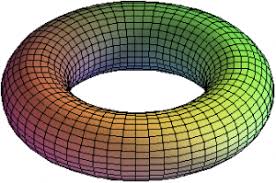
Parlare di Topologia senza parlare di spazi connessi è assurdo. Ho perciò dovuto introdurre due articoli sulla connessione. Poi potremo vedere come matematizzare il nastro, ovvero scoprire cosa significa "incollare" in senso matematico.
Questo quiz è stato proposto come introduzione ad un argomento molto importante in topologia: la connessione. Sto mettendo infatti a punto un articolo in topologia generale su questo argomento. Ma anche in teoria dei grafi la connessione è un argomento importante e prevede anche molte similitudini con la topologia. Riprendo la definizione di grafo data inizialmente qui, in […]
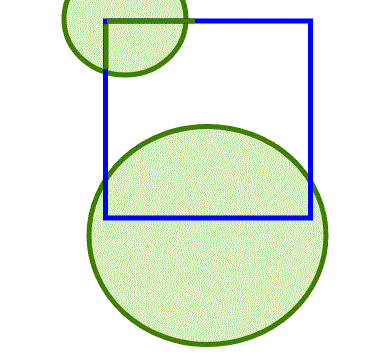
In questo articolo tratteremo la vera magia della topologia; gli Omeomorfismi. Queste trasformazioni fra spazi topologici sono in grado di trasformare un cerchio in un quadrato e una sfera senza poli in un cilindro! Provare per credere..
Questo articolo presenta un problema Topologico. Problema non facile, ma la cui soluzione è veramente alla portata di tutti: basta solo sapere la differenza fra un numero pari e un numero dispari,e tanta buona volontà. Non richiede nessun'altra conoscenza matematica. L'argomento è il punto di partenza della teoria dei Grafi.
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica Nella prima puntata di questa serie di articoli abbiamo parlato di spazi metrici, di bolle,di insiemi aperti e continuità. Il risultato più importante è stato quello di aver dimostrato l' equivalenza fra due distinte definizioni di continuità fra spazi metrici:la prima, che è la più conosciuta ed […]
In questo articolo confluiscono, con alcune integrazioni, i contenuti del quiz “Art attack” e dell'articolo “Percezioni illusorie nella visione e nell'arte” presenti in altre sezioni del blog.
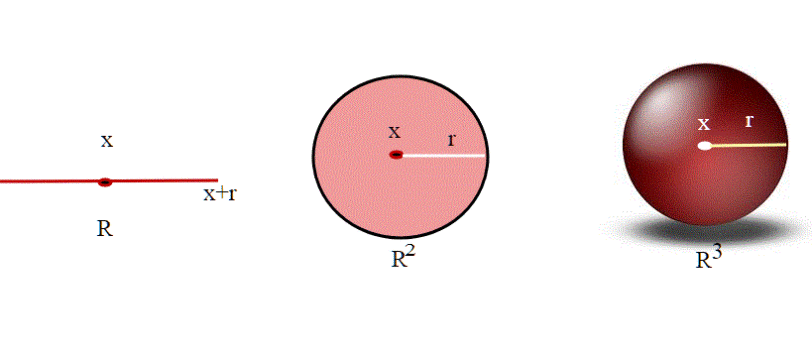
Recentemente abbiamo visto degli interessanti articoli su quella che si definisce "sartoria topologica" . Questo è il primo di una serie di articoli che ci porterà a capire come è possibile generare matematicamente figure geomatriche tipo il nastro di Moebius senza usare carta e colla.. il percorso non sarà immediato ma nemmeno troppo complesso.
Definire “soluzione” le considerazioni che esporremo è decisamente esagerato. Non forniremo dimostrazioni formali ma solo osservazioni e ragionamenti da esse derivati, per capire come si sono “intrecciate” le cose.
Partiamo dalla madre di tutte le strisce e coloriamo una delle sue facce di verde, lasciando bianca l'altra faccia ...
In questo quiz non sono richiesti calcoli matematici, né statistici, né dovrete ricordare teoremi di geometria o regole di logica. (mi pare di sentire un sospiro di sollievo provenire dal fondo del Teatro ...)
Si tratta solo di eseguire semplici operazioni manuali e riflettere sui risultati ottenuti. Una specie di gioco di prestigio, una scoperta di comportamenti inattesi e curiosi.
- 1
- 2