Ciò che appare vicino nel Cosmo potrebbe essere invece lontanissimo a causa della visione bidimensionale che noi abbiamo della Sfera Celeste. In questo caso, però, la realtà conferma l'apparenza e insegna a capire come e dove nascono le stelle.
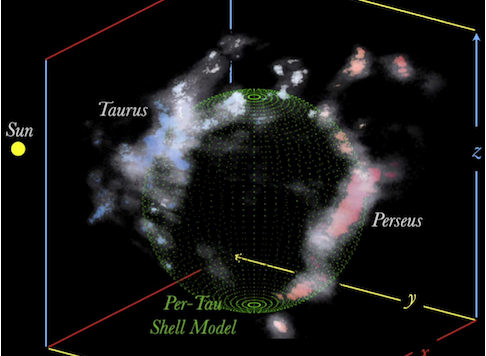

Ciò che appare vicino nel Cosmo potrebbe essere invece lontanissimo a causa della visione bidimensionale che noi abbiamo della Sfera Celeste. In questo caso, però, la realtà conferma l'apparenza e insegna a capire come e dove nascono le stelle.

Ormai conosciamo (teoricamente soprattutto) la struttura di un buco nero galattico attivo. Ci riferiamo, in pratica, agli AGN (Nuclei Galattici Attivi), i veri cannibali nelle tradizioni popolari. Tuttavia, molte cose sono ancora da confermare e, principalmente, la causa delle differenze di emissione che mostrano a varie lunghezze d'onda. Fondamentale era poter inserire nel quadro, in modo definitivo, una particolare "ciambella" che contenesse il buco nero vero e proprio.
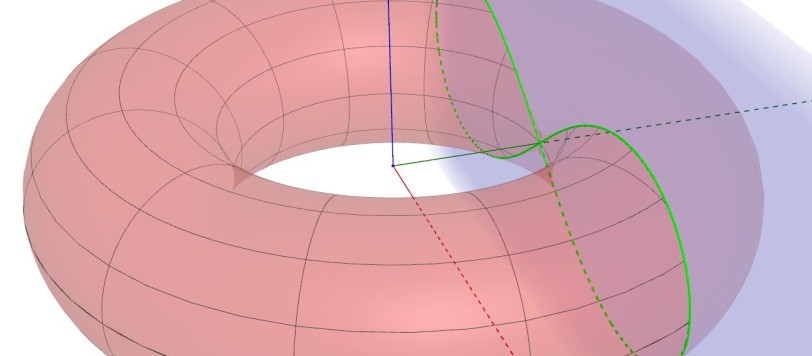
Rieccoci qui con l'ultima parte dell'appendice all'articolo 8° sulla geometria solida, dedicato al toro. Nella prima appendice abbiamo fatto la conoscenza delle circonferenze di Villarceau. In questa seconda appendice illustrerò altre interessanti curve ottenibili andando a sezionare il toro con un particolare piano. Ci serviremo, come sempre in geometria analitica dello spazio, del linguaggio della matematica. Ma niente paura, useremo strumenti semplici. E, in ogni caso, se avete dubbi, non avete che da chiedere nei commenti.
L'ultima volta avevo concluso l'articolo accennando alle sezioni spiriche, che sono proprio quelle di cui ci occupiamo questa volta. Intanto, perché si chiamano spiriche ?
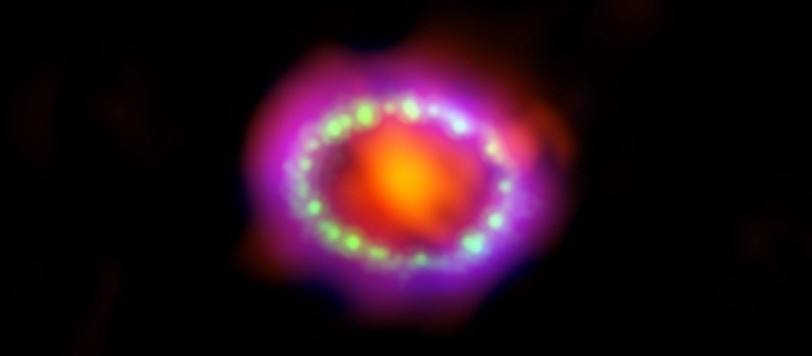
Non è certo comune vedere un fenomeno dell'Universo che mostra cambiamenti ben percettibili anche in tempi umani. Uno splendido esempio è dato dall'esplosione di una supernova e lo è ancora di più se essa è praticamente una vicina di casa. Ecco come è variata una ciambella nata nel 1987...
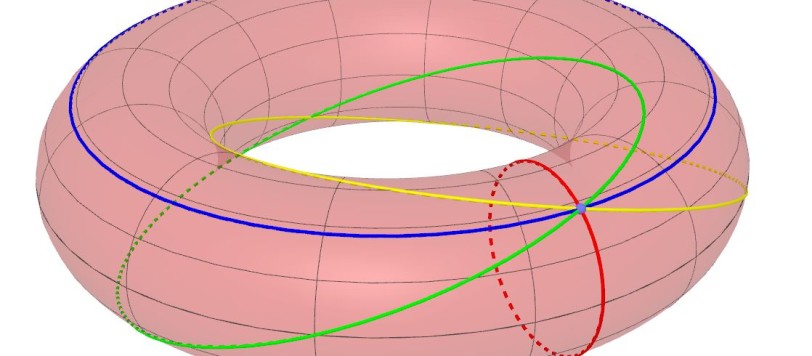
In questa appendice all'articolo sul toro analizzeremo le curve risultanti dalla sezione del toro con determinati piani secanti. Scopriremo le bellissime circonferenze di Villarceau, l'ippopede di Proclo , gli ovali di Cassini, le lemniscate di Booth e di Bernoulli. Vedremo come la geometria solida sa regalarci momenti di autentica meraviglia. L'appendice è divisa in due parti. La prima è dedicata alle sole circonferenze di Villarceu.