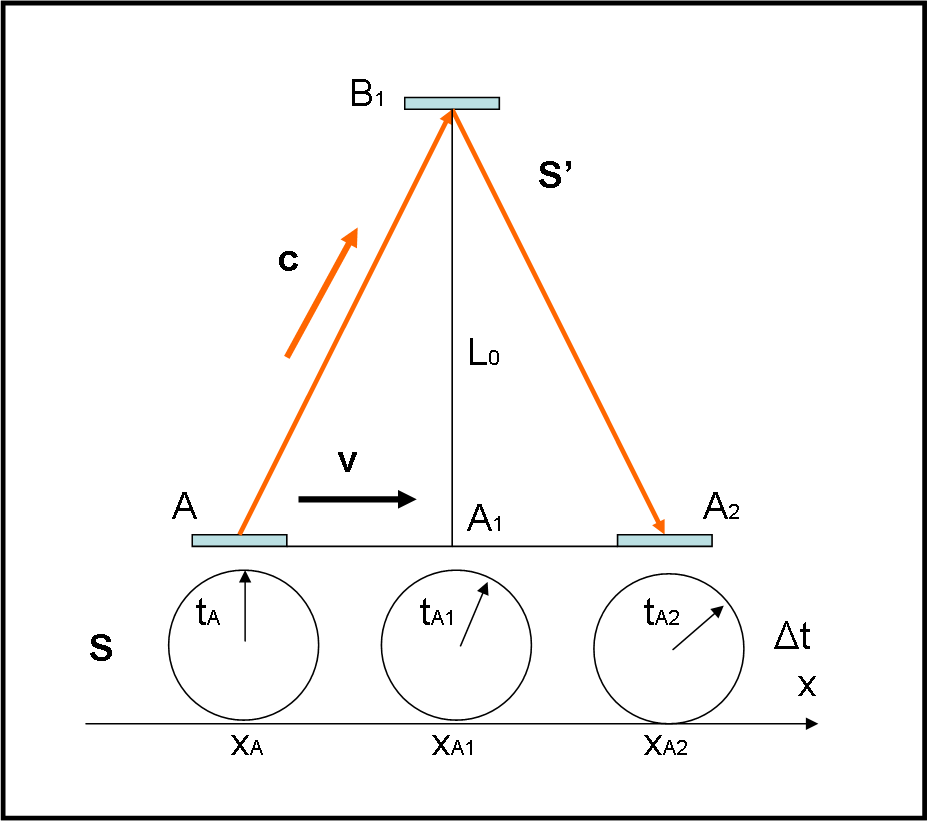
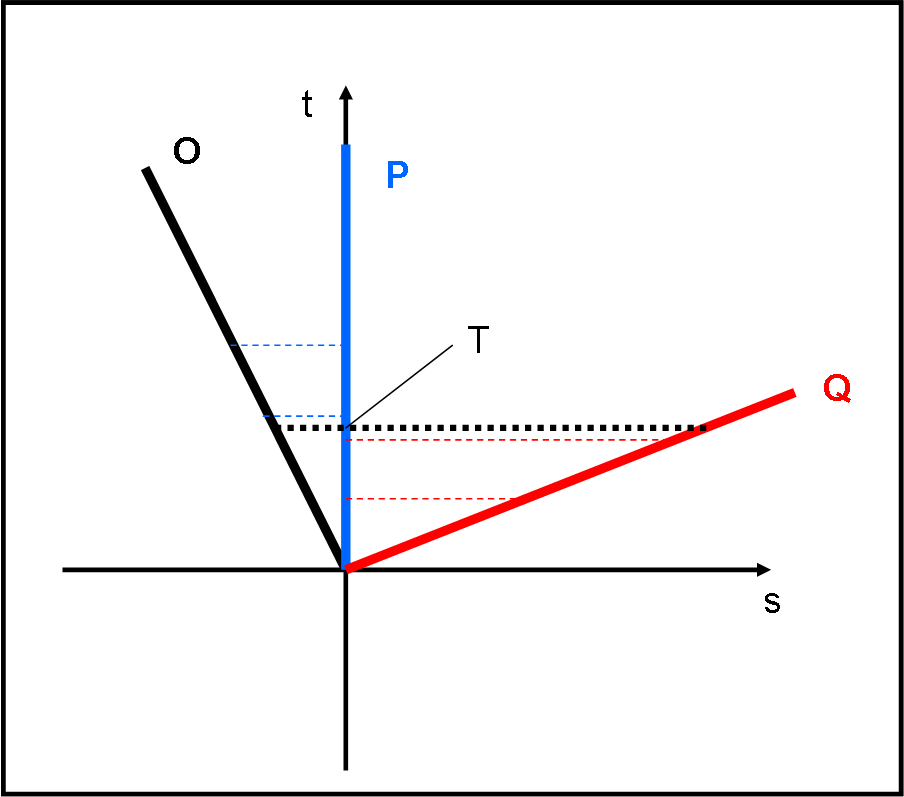
Questa è la prima parte della Teoria della Relatività Ristretta o Speciale. Si parte dalla relatività galileiana e si arriva agli effetti che derivano dai postulati di Einstein: dilatazione dei tempi e contrazione delle lunghezze. Facciamo conoscenza con la trasformazione di Lorentz , il passo fondamentale per passare da spazio e tempo a spaziotempo. Ricordiamo che l'intera teoria si riferisce SOLO a sistemi di riferimento in moto rettilineo uniforme tra loro. Non sono quindi valutate le deformazioni spaziotemporali causate dalla gravità e dalla sua accelerazione. La relatività ristretta è quindi una teoria perfettamente simmetrica e niente ha a che vedere con le deformazioni univoche causate dalla relatività generale. Negli articoli seguenti, si toccheranno le ripercussioni della relatività ristretta sulle varie grandezze fisiche (tra cui la celebre E = mc2) e la sua rappresentazione nel diagramma spaziotemporale di Minkowski.