Maurizio è stato velocissimo nello "scardinare" il problema. Io riporto la via forse più semplice, passando ancora una volta alle tre dimensioni.


Maurizio è stato velocissimo nello "scardinare" il problema. Io riporto la via forse più semplice, passando ancora una volta alle tre dimensioni.
Un classico paradosso che, per molti, non è ancora stato risolto. Ma è veramente un paradosso o solo una specie di fake news?

Ancora sulla sezione aurea, ma mettendo in luce un'altra piccola dimenticanza di Euclide & Co.
Ottimo Andy e anche Albertone, anche se alla fine vuole trovare r e non l'area minima... Riporto comunque una soluzione decisamente semplice, che rispecchia quelle proposte dai nostri amici.

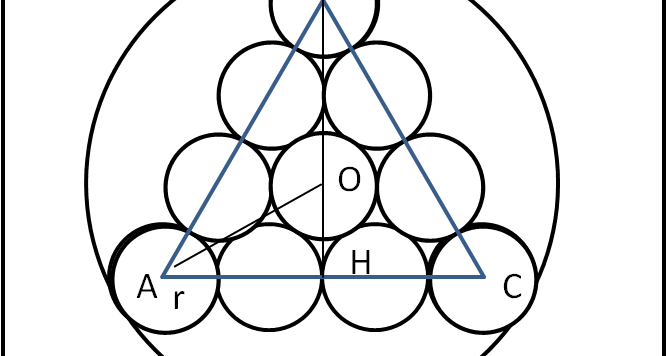
Il quiz dei due cerchi, "incatenati" al triangolo equilatero, sembra aver perso di interesse. Peccato... perché proprio la seconda parte è quella più interessante, che ci permette addirittura di enunciare un "nuovo" teorema, simile a tanti ricavati dai greci antichi. A quanto mi risulta non mi sembra che sia mai stato enunciato, ma potrei sbagliarmi. Comunque un piccolissimo tassello geometrico in più del nostro circolo.

Riporto la soluzione della prima parte, ma lascio ancora in sospeso la seconda parte, quella più "giapponese". Il quiz, quindi, continua.

E' un periodo che sforno tanti quiz e sono contento di vedere che riscuotono successo. Anzi, mi accorgo che, a volte uno a volte un altro, siete prontissimi a rispondere. Voglio provare a divertirmi anch'io, sicuro della vostra partecipazione!
Le prodezze del Teorema di Tolomeo proseguono, aiutandoci a dimostrare facilmente una proprietà poco conosciuta collegata ai triangoli equilateri e a finire in bocca alla sezione aurea. Con questo articolo finiamo la nostra piccola-lunga storia sul Teorema di Tolomeo, ma non è detto che non ci si ritorni su, prima o poi.

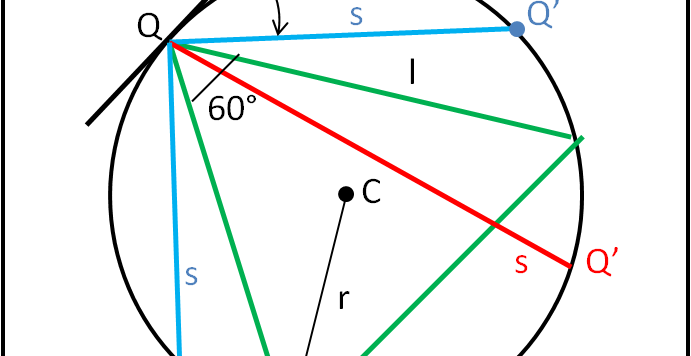
Andy ci ha mostrato come il problema, apparentemente abbastanza difficile, sia risolvibile con pochi passaggi. Noi lo impostiamo in modo un po' diverso, risolvendolo con una sola rotazione di 60°. Un approccio di estrema "eleganza".

Questo articolo è un piccolo capolavoro di logica ed eleganza (non certo per merito mio…). Vi invito a leggerlo senza paura. Esso presenta la determinazione dei punti lagrangiani L4 e L5, nel modo più generale possibile, seguendo la strategia illustrata nel 1999 da I. Vorobyov dell’Università di Vienna. Un metodo di una semplicità disarmante, che io ho solo cercato di arrangiare in modo veramente elementare (matematica e geometria delle scuole medie).