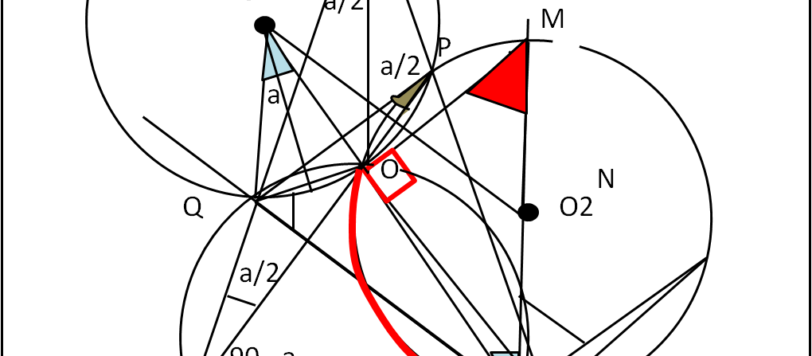
Riporto una soluzione, ma, come discusso nei commenti, ve ne sono sicuramente altre, forse più veloci...
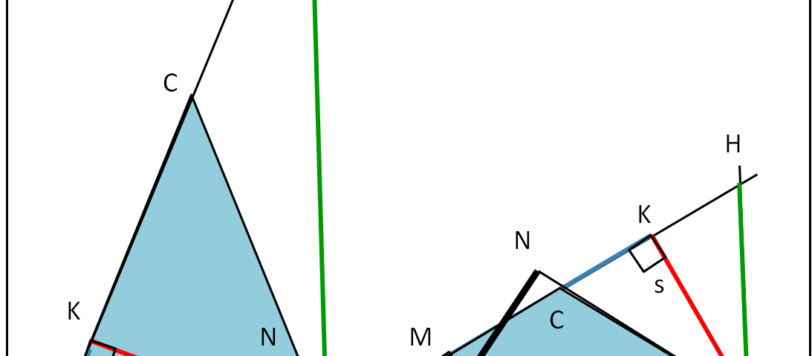
Bravi Andy, Arturo e Leandro che hanno risolto il problema, mentre noi abbiamo imparato una nuova proprietà del triangolo isoscele.
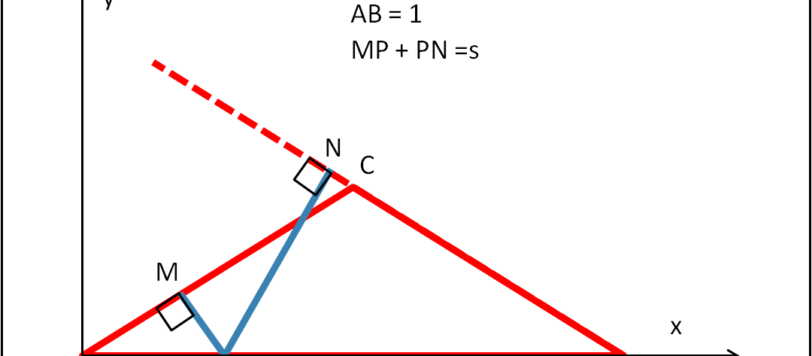
Dopo nuclei che si divertono a rompersi e a unirsi, treni che fischiamo, evoluzione cosmologica, torniamo alla cara geometria (Euclide si è un poco alterato della vostra poca passione a riguardo...).
Il più difficile dei problemi facili. Provate con i vostri figli e/o nipoti e potrete vedere quanto la tecnologia della "pappa pronta" può aver influito sulla loro preparazione scolastica.
Cari amici, la generalizzazione del problema iniziale mi ha portato a cercare una nuova strada per descrivere il "fenomeno" geometrico. Una strada che mi è sembrata molto interessante e, all'apparenza almeno, del tutto inesplorata. Il bello è che potrebbe essere resa benissimo da una animazione (vero Arturo?) o permettere di costruire un qualche aggeggio concreto (vero Frank?). Fatemelo dire: possiamo chiamarlo "l'ultimo (ma anche il primo!) teorema di Zappalà o, meglio, di Zappalat" e che Fermat non me ne voglia!
Il teorema di Talete porta con sé un po' di ambiguità, dato che quello che noi italiani chiamiamo "teorema di Talete" è diverso da quello "inglese". Dimostriamo quest'ultimo e ci accorgeremo che si devono dimostrare anche altri enunciati, che siamo soliti dare per buoni. Un'interessante modo per capire quanta logica ci sia nelle scoperte geometriche degli antichi greci (ma non solo loro, anche degli indiani, dei cinesi, degli arabi...)
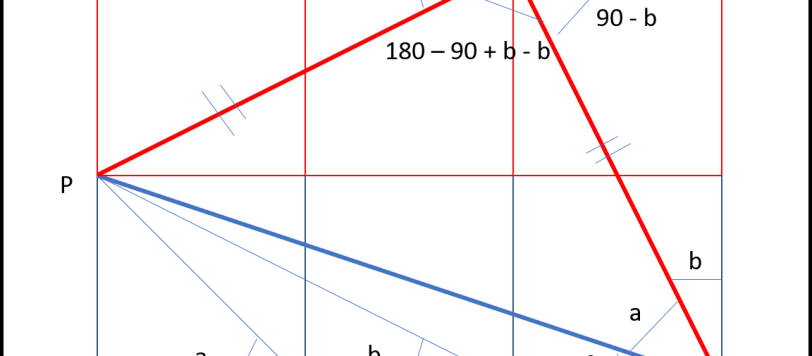
Beh... cari amici, devo dire che il nostro Oreste Pautasso ha cercato veramente di presentarci tutti i 54 metodi di risoluzione della prima parte. Abbiamo dovuto abbatterlo dall'albero su cui si era rifugiato per farlo smettere. Ovviamente, per partito preso e per alto senso democratico, nessuno dei suoi metodi può essere considerato "elegante" come quello che avevo in mente io!
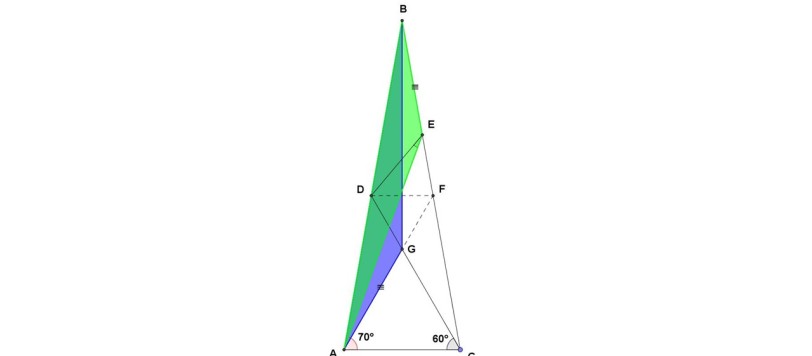
Egr. sig. Oreste Pautasso,
siamo lieti di annunciarLe di essere riusciti a calcolare l'angolo che formano i raggi del Sole quando entrano in quella misteriosa piramide della quale gli archeofili di Cuneo hanno scoperto una raffigurazione in un'antica pergamena! Il bello è che lo abbiamo fatto senza bisogno di arrampicarci per misurarlo col goniometro, ma utilizzando quelle meraviglie che si chiamano matematica, geometria e trigonometria. E, siccome ci piace fare le cose per bene, abbiamo utilizzato metodi diversi per arrivare allo stesso risultato, così non avrà dubbi sul fatto che l'angolo calcolato sia proprio quello giusto!
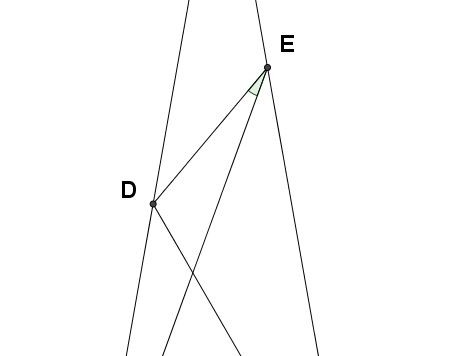
Vi proponiamo un quiz di geometria piana che ha attirato la nostra attenzione perché si presta ad essere risolto seguendo strade diverse. Anche stavolta ve lo proponiamo per mezzo del nostro simpatico amico Oreste. Eccovi la lettera che ci ha fatto pervenire...
IN CALCE AL QUIZ UN SUGGERIMENTO INSERITO IL 27/2/2017
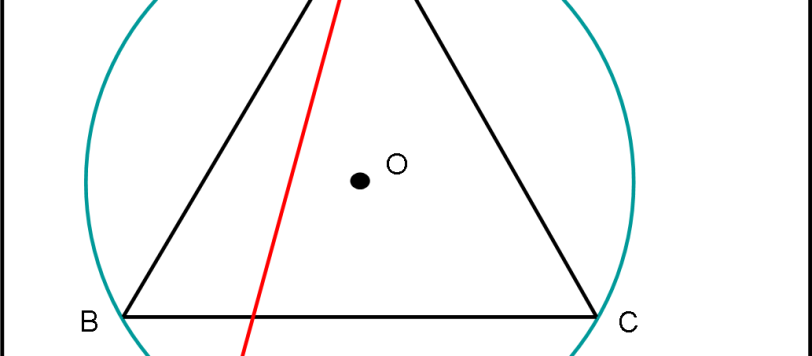
Non vorrei sembrare troppo arrogante… ma, questa volta, l’apprendista stregone cerca di sfidare il club dei maghi (ma non solo loro). Abbiamo bisogno soltanto di una circonferenza e di un triangolo equilatero. I procedimenti per ottenere la soluzione sono molti e quindi potrebbe diventare un vero "tormentone", come già successo per altri quiz.
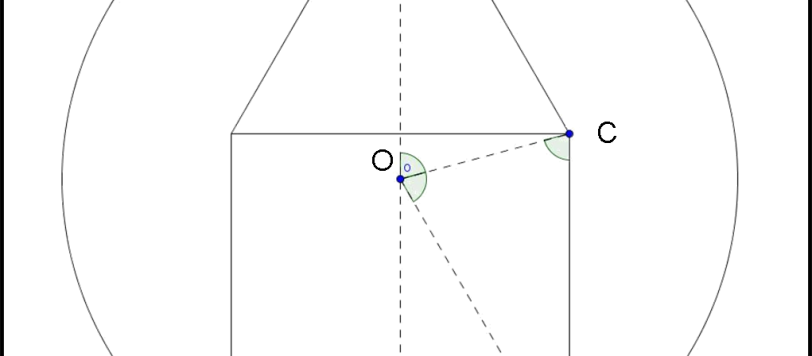
Le soluzioni sono state molteplici, ma devo ammettere che il metodo utilizzato da Arturo è decisamente il migliore. Può darsi che si possa risolvere più velocemente, ma non riesco a trovare niente di meglio. Se qualcuno ci riesce, tanti complimenti! Come soluzione riporto, quindi, pari pari quella scritta nel commento di Arturo… Bravi tutti, comunque!