Un esercizio molto utile per comprendere al meglio i momenti d'inerzia e quelli angolari.
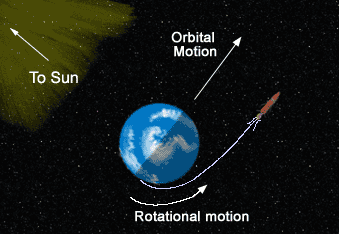
Un'altra ciliegina nata durante uno scambio di commenti con Alberto parlando di effetto fionda. La faccenda si era risolta, ma penso non sia male trasformarla in uno dei saporiti frutti sotto spirito...
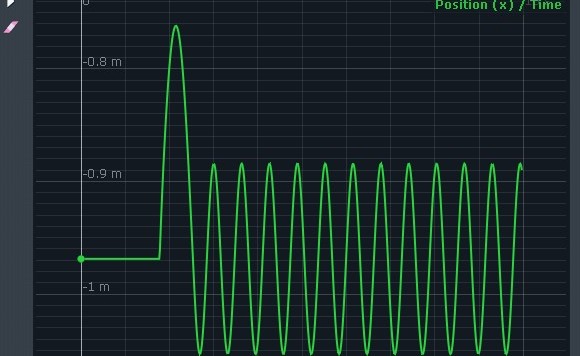
Soluzione al quiz sull'urto ammortizzato Per rispondere ai primi tre quesiti del quiz conviene seguire la via "energetica". Nella fase iniziale, cioè quando abbiamo solo la massa m1 in moto rettilineo uniforme con velocità v1, l'energia meccanica del sistema è data dalla sola energia cinetica posseduta dalla massa m1: Osserviamo ora , "alla moviola", l'evolversi […]

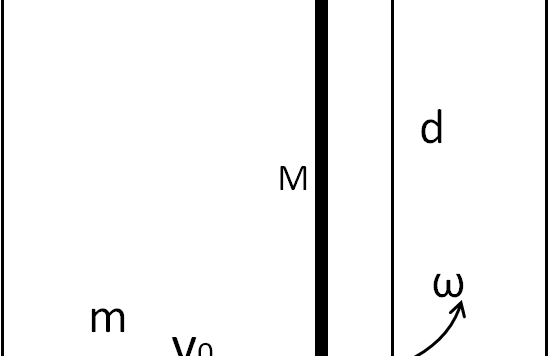
Urto.... con ammortizzatore Abbiamo una massa m1 che scorre senza attrito con velocità v1 lungo un piano orizzontale verso una seconda massa m2. Quest'ultima è inizialmente ferma ed è collegata all'estremità sinistra di una molla ideale di costante elastica k , a sua volta fissata, nella sua estremità destra, ad un blocco inamovibile. Inevitabilmente, ad […]
Dopo tanta relatività, torniamo un po’ alla fisica classica con un quiz tipicamente papalliano. Si chiedono varie risposte, che necessitano di un minimo di dinamica (classica) e qualcosa di matematica (un bel ripassino). I più bravi… aspettino qualche giorno.
Diamo la soluzione del quiz relativistico destinato ai solutori più che abili. Le risposte date erano praticamente tutte giuste, cosa di cui non mi stupisco, visti i ... concorrenti. Mi sarebbe piaciuto, però, vedere qualche tentativo in più...
Un paio di grafici illustrativi e un piccolo paradosso, proposto anch'esso da Feynamn, che introduce prepotentemente nell'equivalenza di massa ed energia (come vedremo meglio più in là).
Questo esercizio non è assolutamente necessario per proseguire nella dinamica relativistica. E’ un “di più” che può essere utile per mettersi alla prova sulla RR e per prepararsi in anticipo alla discussione sull’uguaglianza tra massa ed energia, caposaldo einsteiniano. In questo “quiz” vogliamo fare qualcosa di molto simile a quanto ottenuto nell’ultimo capitolo sulla dinamica […]
A qualcuno potrebbe sembrare che io stia sollevando un sacco di problematiche concettuali e di ostacoli, nel tentativo di descrivere correttamente la quantità di moto relativistica. In giro per la rete si trovano determinazioni velocissime e che -a prima vista- sembrano del tutto logiche… sicuramente più rapide e semplici del procedimento che ho iniziato a descrivere con molta precauzione. Attenzione, però...

Questo quiz non ha avuto molto successo (pochissimi lettori). Forse i quiz sono diventati troppo frequenti. Va bene, sospendiamo per un po’… Comunque sia, diamo la soluzione che si articola in due fasi e introduce un concetto importantissimo in meccanica: il pendolo balistico. Dapprima il papallo deve calcolare la distanza d attraverso un po’ di facile trigonometria e poi deve diventare lui stesso un pendolo balistico appendendosi a un ramo con la corda e facendosi sparare addosso un proiettile con una velocità perfettamente calcolata attraverso la conservazione della quantità di moto e dell’energia