Ho trasformato il quiz sul carrello in un problema risolto passo dopo passo. Quello che è necessario sapere è stato trattato con tutti i particolari nel nostro Circolo (vedi archivio).

Ho trasformato il quiz sul carrello in un problema risolto passo dopo passo. Quello che è necessario sapere è stato trattato con tutti i particolari nel nostro Circolo (vedi archivio).
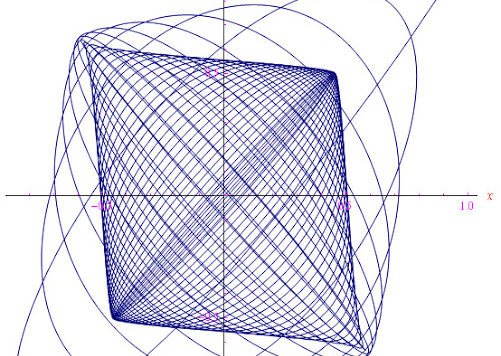
In questa prima parte torniamo un po' all'antica... ai bei tempi in cui cercavo di spiegare l'analisi matematica, con tanto di derivate e integrali, in modo comprensibile a tutti coloro dotati di voglia di imparare e di conoscere, per avendo basi di partenza molto basse (che male c'è?). Iniziamo perciò in modo veramente elementare e ci portiamo rapidamente e facilmente a maneggiare le celebri e bellissime figure di Lissajous. Per far contenti coloro che usano dire: "Sì, belle... ma a che servono?" toccheremo le applicazioni che le hanno portate ad essere fondamentali nel posizionare velivoli spaziali che necessitano di condizioni stabili e non vicinissime alla Terra. E se ce la sta facendo l'uomo, potete giurarci che non se l'è certo fatto scappare madre Natura!
Uno dei tipi di telescopio più famosi porta il nome di uno scienziato altrettanto famoso. La sua caratteristica principale è l’obiettivo formato da uno specchio che ha una particolare forma, capace di eliminare un certo tipo di difetto che limita le prestazioni del suo compagno “sferico”. Teoricamente (ma anche praticamente), chiunque può costruire “in casa” questo tipo di obiettivo (il metodo è stato utilizzato professionalmente).
Un non-quiz per conoscere sempre meglio le nostre amiche stelle, rispolverando un semplice concetto di fisica classica!
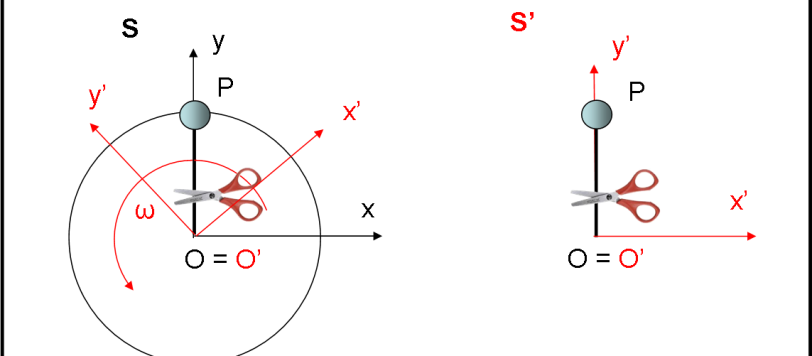
Dopo esserci esercitati con i sistemi inerziali, proviamo a fare un passo in avanti e introduciamo un sistema rotante. Il gioco si complica un poco, ma ritroveremo una cara amica conosciuta da poco…
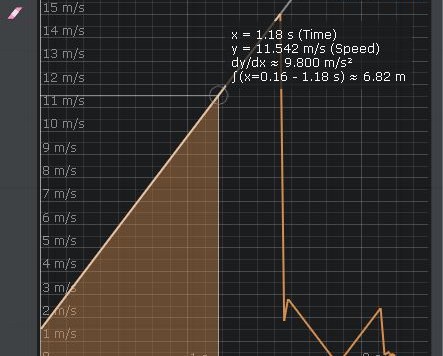
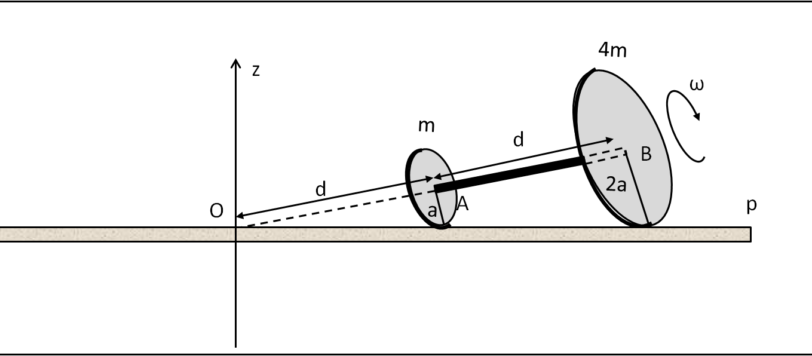
Grazie a tutti coloro che hanno manifestato interesse per questo quiz, attestato dall'elevato numero di visite, e a coloro che hanno partecipato con le proprie risposte. La risposta alla domanda posta dal quiz è affermativa. L'occorrente per far cadere più lentamente il disco cilindrico è già tutto presente e non ci serve altro. Basta solo […]
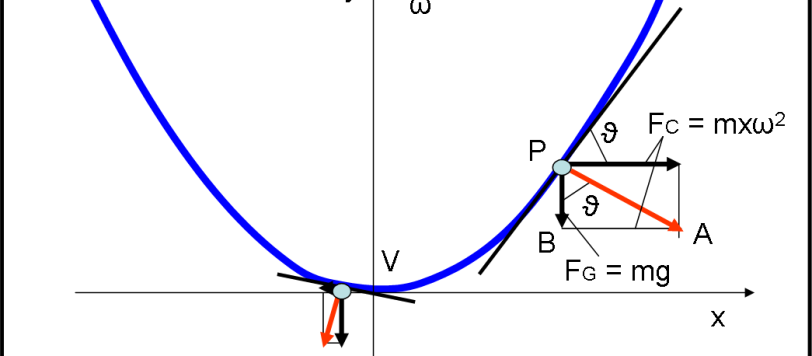
Riportiamo la soluzione del quiz che va oltre alla semplice spiegazione e che apre interessanti sviluppi sia per la fisica newtoniana che per l’ottica geometrica applicata ai telescopi. Un articolo da leggere… e con un nuova proposta di quiz.
Finora abbiamo ragionato in termini di periodi sinodici (un’utilissima scelta data la loro osservabilità), ma possiamo descrivere gli stessi risultati lavorando con i periodi siderali e con le velocità angolari. Questo approccio ci viene utile per gli allineamenti che escludono il Sole.

Il problema descritto è quello decisamente importante in fisica, detto del "pendolo conico". Ha risposto solo Alvy (bene)… pazienza… Tuttavia, riporto la soluzione con alcune considerazioni sulla funzione che lega la velocità angolare con l’angolo di apertura della giostra. Aggiungo anche una piccola appendice.