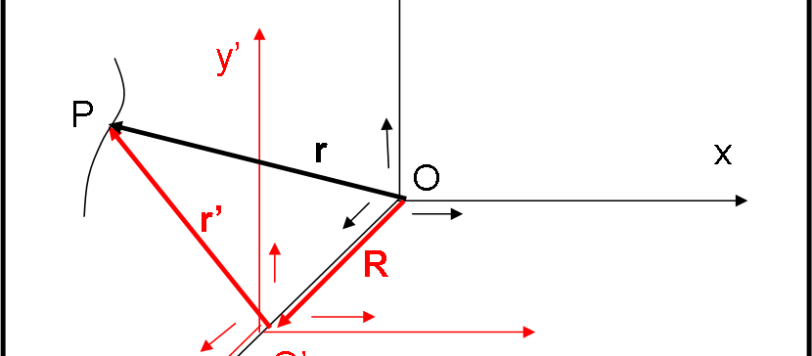
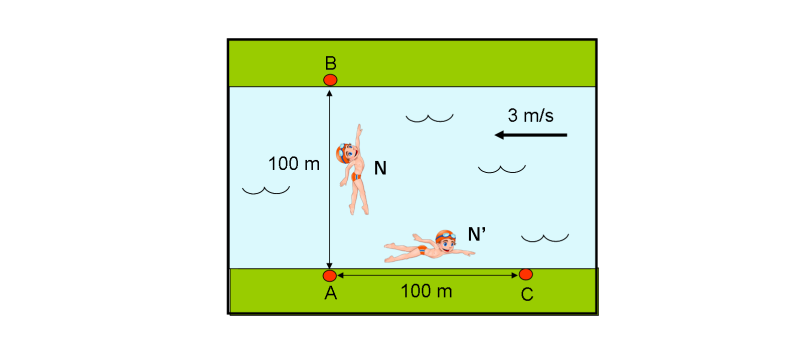
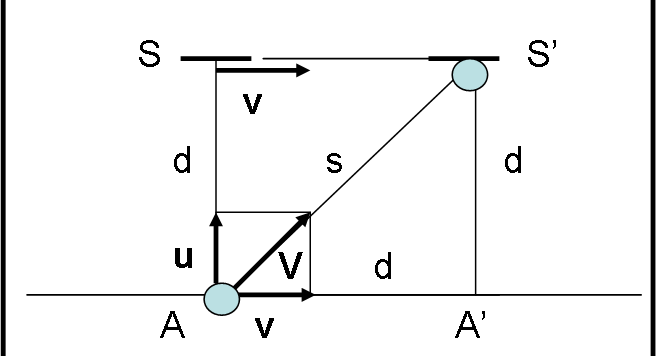
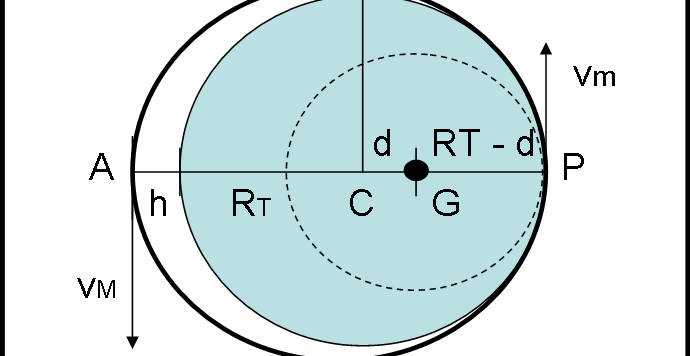
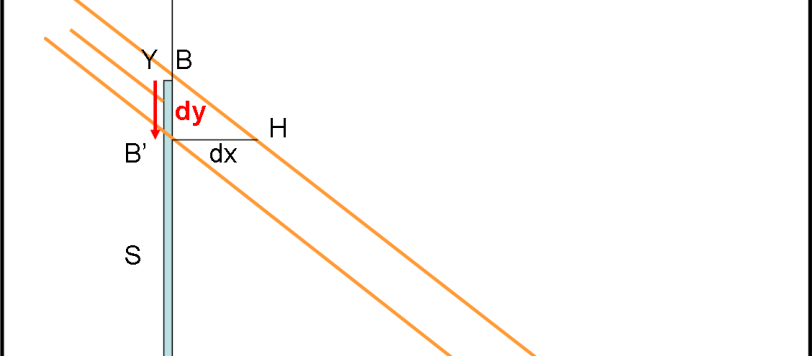
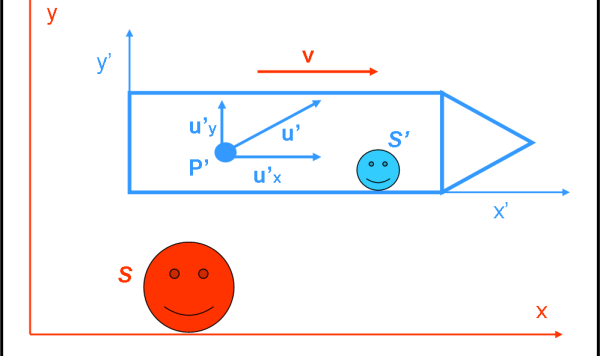
Beh... Coriolis non ha aspettato tanto (oggi ho deciso di lavorare solo di testa e non di braccia...). Per cui, ecco la nuova versione della prima parte della trattazione della forza di Coriolis, estesa e sicuramente più completa. Fa sicuramente uso di un po' di matematica semplice e recupera nozioni sui versori, vettori, prodotti scalari e vettoriali. Una bella rinfrescata non farà male... Il risultato, però, è estremamente utile per capire al meglio la "nascita" delle forze fittizie in generale. Lo scopo va, quindi, ben oltre la forza di Coriolis.