Questo articolo, che arriva per ultimo, avrebbe dovuto essere il primo, in quanto “cerca” di introdurre la Relatività Generale da un punto di vista abbastanza particolare, che, però, assomiglia sicuramente al carattere fanciullesco di Einstein. Un metodo saltellante e poco logico? Beh… anche in questo senso ho cercato di avvicinarmi alla formulazione di Albert, che, in fondo, non sapeva nemmeno lui cosa cercare e come cercarla. Aveva solo grandi dubbi e qualche domanda molto semplice, semplice come l’intero Universo. Un uomo vero, un figlio del Cosmo, forse il solo che parlando lo stesso linguaggio, poteva superare un confine apparentemente insuperabile.

Mentre, piano piano e con molta attenzione, cerco di unire tutti i pezzi della Relatività Generale (in fondo, ha fatto così lo stesso Einstein), vediamo di divertirci con qualche effetto particolare della sbalorditiva formula e delle equazioni che comporta. Non tutte sono state sicuramente risolte e la RG può ancora regalarci scoperte inattese (o quasi). Perché non tornare nel 2016 o anche prima? Viaggiare nel tempo potrebbe aver bisogno solo di un cilindro…
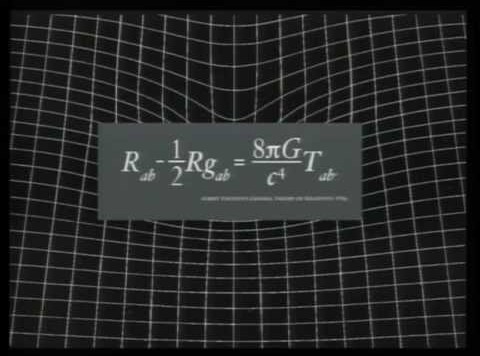
Siamo giunti alla formula risolutiva, a quella che lega curvatura con massa/energia. Curvato il tempo, dovremo affrontare una piccola lotta tra RR e RG per descrivere il moto di tutto ciò che finisce nei pressi di una massa con una densità importante. Anche la luce deve inchinarsi alla legge forse più rivoluzionaria della Scienza.

Poche frasi di riflessione, ribaltando la storia della fisica. Ultimamente Newton (anche se in maniera ironica e scherzosa) è stato trattato alquanto male e sta facendo la figura dello sprovveduto, dell’approfittatore, capace solo di tirare mele ai porci e di prendersele in testa. Mi sento obbligato a spezzare una lancia per lui…

Cari amici, saltellando un po’ e passando da spazio a tempo con voluta noncuranza, siamo arrivati alla conclusione della Relatività Generale, impostata per il lettore medio di questo Circolo.

Un momento di riflessione nella trattazione della Relatività Generale. Potremmo considerarlo un’introduzione, ma anche un riassunto conclusivo. Tutto sta nel come vogliamo entrare nel suo Universo meraviglioso. In un modo o nell’altro, è fondamentale che TUTTI possano essere in grado di avvicinarsi alla più strabiliante teoria del macrocosmo.
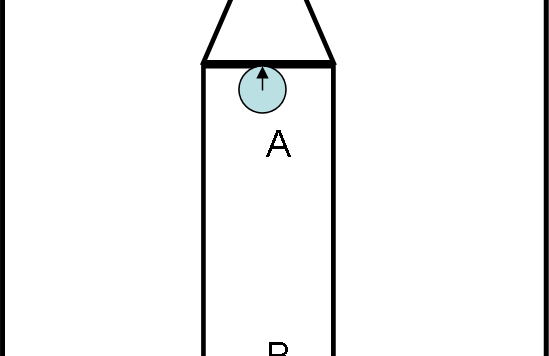
Un altro piccolo, ma fondamentale, passo verso la relatività generale. Il principio di equivalenza che pone sullo stesso piano un sistema accelerato e un sistema sotto l’effetto della gravità comporta conseguenze quasi inaspettate anche sul tempo. La famosa "piastra" torna in campo…
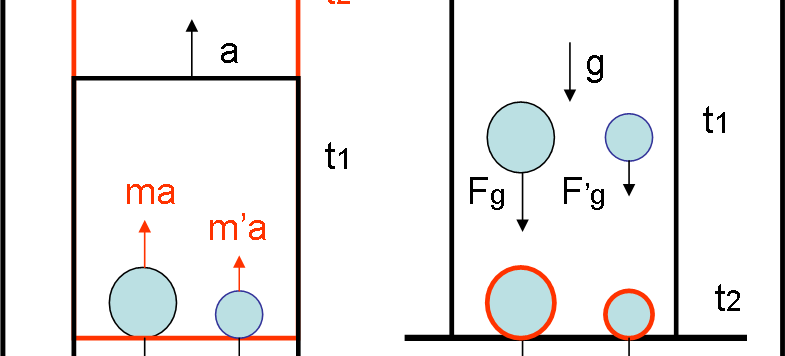
Galileo ha avuto i suoi gravi, Newton ha avuto la sua mela e Einstein ha avuto il suo … imbianchino. Ebbene sì, sembra che l’idea più straordinaria che abbia avuto Einstein (secondo le sue stesse parole) gli sia venuta parlando con un imbianchino che era caduto da un’impalcatura di fronte al suo palazzo. Dopo di allora, forze apparenti, inerzia, accelerazione, gravità hanno iniziato a cambiare completamente la loro descrizione (in pratica sono scomparse) e, allo stesso modo, le conclusioni di Galilelo e Newton sull’uguaglianza “fortunata” di massa gravitazionale e massa inerziale, è diventata l’ovvia conseguenza della gravità.

Non consideriamo questo articolo solo come una semplice soluzione, ma leggiamolo attentamente
perché è oltremodo utile per avvicinarci sempre più alla Relatività Generale e al principio di equivalenza.
Le risposte arrivate sono più che sufficienti per risolvere i tre quiz, ma è giusto pubblicare un articolo che
riassuma le soluzioni, che poi sono, in realtà, una sola: portarsi in un sistema di riferimento in caduta
libera, ossia in balia della sola gravità terrestre.
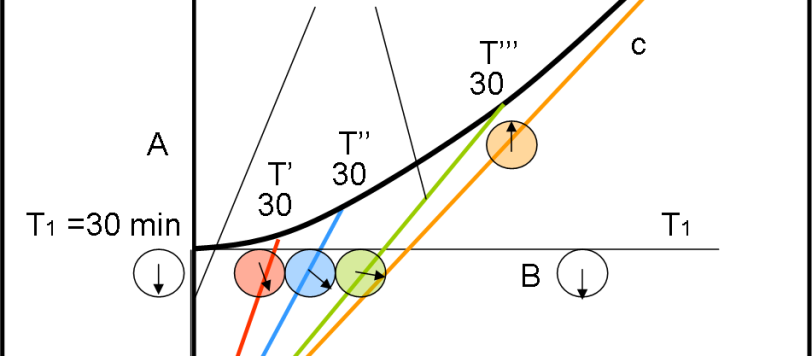
In questo articolo diciamo cose già toccate nella Relatività Ristretta e descritte nel diagramma di Minkowski. Tuttavia, le usiamo per definire in modo chiaro e completo quale sia la linea rettilinea nello spaziotempo. Una conquista non da poco...
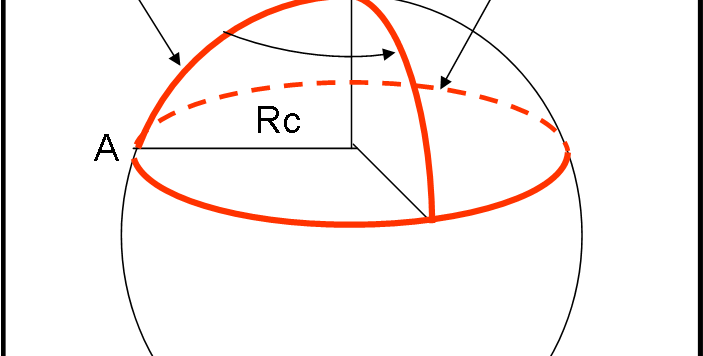
Questo articolo non contiene praticamente formule, ma è decisamente FONDAMENTALE per capire l’essenza più profonda della RG e della sua definizione di spazio tridimensionale curvo. Non perdetelo e non esitate a porre domande se vi rimane qualche dubbio. Capirete anche perché abbiamo perso tanto tempo a spiegare le regole geometriche di una superficie sferica, confrontandole con quelle euclidee e anche perché abbiamo scaldato un piano con una strana piastra. Sembrerà una trattazione addirittura pedante, ma il concetto di curvatura è troppo importante per rischiare di non chiarirlo completamente.

Abbiamo discusso a lungo della curvatura di uno spazio a due dimensioni e abbiamo visto come la geometria che lo descrive si discosti completamente da quella euclidea che impariamo a scuola. Come detto varie volte, la curvatura di uno spazio (lasciando da parte il tempo, almeno per adesso) è legata strettamente alla relatività generale, un argomento che aspetta ancora di essere affrontato in modo diretto e decisivo. Vale la pena capire ancora meglio cosa si intende per “curvatura”

Questo lungo articolo riunisce tutti quelli relativi alla geometria sferica. Esso è stato anche inserito tra gli approfondimenti.
Beh… è bastata l’intrusione di Alvy (era ora!), l’accenno di Umberto e il solito problema di chi parla tanto senza volere prima studiare (non mi riferisco certo a voi!), ed ecco che la frittata è fatta. No, non parlerò di Relatività Generale, ma dell’angoscioso problema del destino dell’Universo e, quindi, della sua “forma”… Attraverso qualche formula che è alla portata di tutti coloro che abbiano digerito la matematica illustrata finora (ma anche meno), ricaviamo nientemeno che la densità critica, data solitamente come risultato di equazioni ben più complicate (ne parleremo quando faremo la relatività generale).
Questo articolo ci mostra, qualitativamente, come la relatività generale implichi una curvatura dello spaziotempo e non solo dello spazio. Purtroppo, noi intuiamo abbastanza bene solo la seconda. Limitandosi ad essa la relatività sarebbe un’assurdità. Non ci sono formule, ma il concetto non è banalissimo, benché fondamentale per immergersi veramente nella problematica dei buchi neri e non solo. Non fatevi ingannare dall’apparente banalità: se capite l’essenza del concetto di base, tutto sarà più facile.
Chi non ha mai visto una delle figure più usate in letteratura per rappresentare i buchi neri come deformazioni dello spazio-tempo? Mi riferisco ai celebri “imbuti”. Una geniale descrizione grafica che deve essere, però, capita con tutti i suoi enormi limiti. Cerchiamo di costruirla e di capire quanto sia “fittizia” e quanta confusione potrebbe creare se non interpretata correttamente.
- 1
- 2

