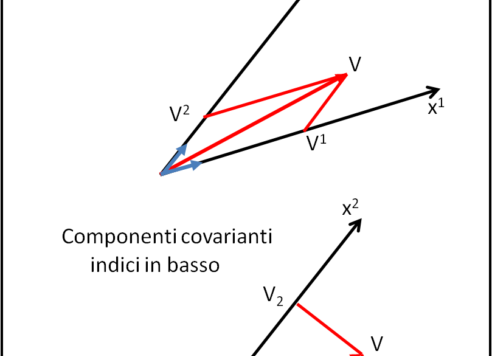
E' ora di trasformare i tensori e di introdurre, in modo estremamente didattico, le coordinate controvarianti e covarianti. Le cose si complicano un poco e devo limitarmi a dare alcune definizioni ...
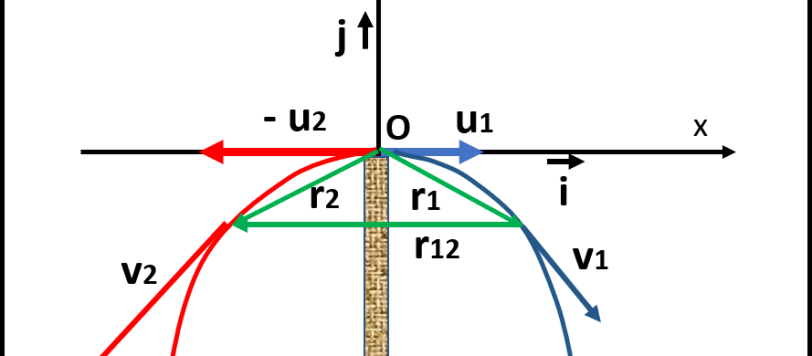
Un problema che si risolve molto elegantemente lavorando solo con i vettori (e i versori), ricordando una classica operazione tra di loro.
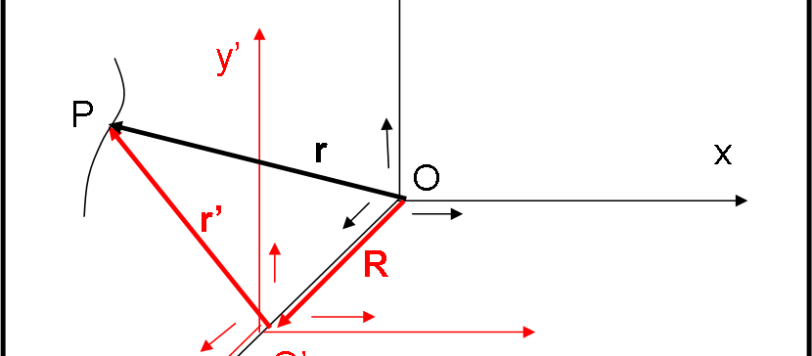
Beh... Coriolis non ha aspettato tanto (oggi ho deciso di lavorare solo di testa e non di braccia...). Per cui, ecco la nuova versione della prima parte della trattazione della forza di Coriolis, estesa e sicuramente più completa. Fa sicuramente uso di un po' di matematica semplice e recupera nozioni sui versori, vettori, prodotti scalari e vettoriali. Una bella rinfrescata non farà male... Il risultato, però, è estremamente utile per capire al meglio la "nascita" delle forze fittizie in generale. Lo scopo va, quindi, ben oltre la forza di Coriolis.
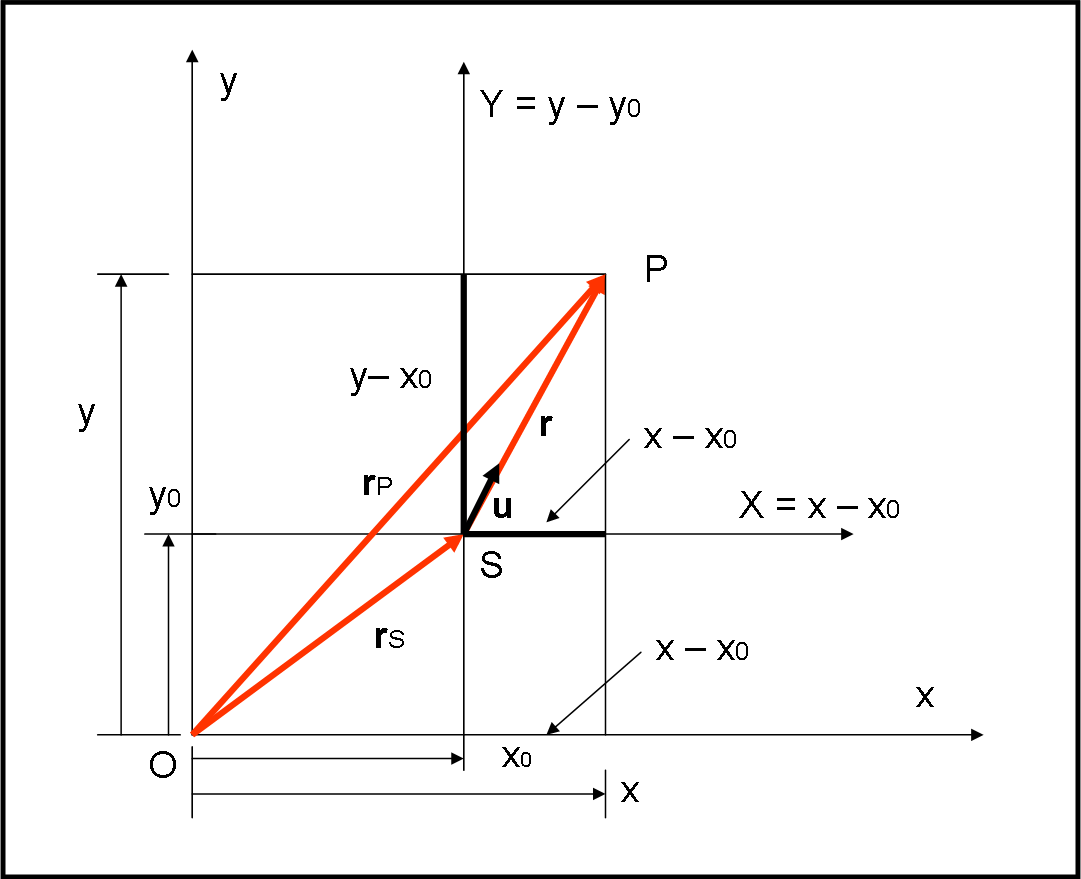
Dedichiamoci al problema più “difficile”, ossia a quello di ricavare il moto ellittico partendo dalla leggi di Newton. Ci accorgeremo che prima di arrivare alla fine, incontreremo già la seconda legge di Keplero, oltre che fare amicizia con un piano. In questa prima parte ci fermeremo proprio su questo piano. Procediamo con molta lentezza e chiarezza. Alla fine il moto orbitale avrà ben pochi segreti...
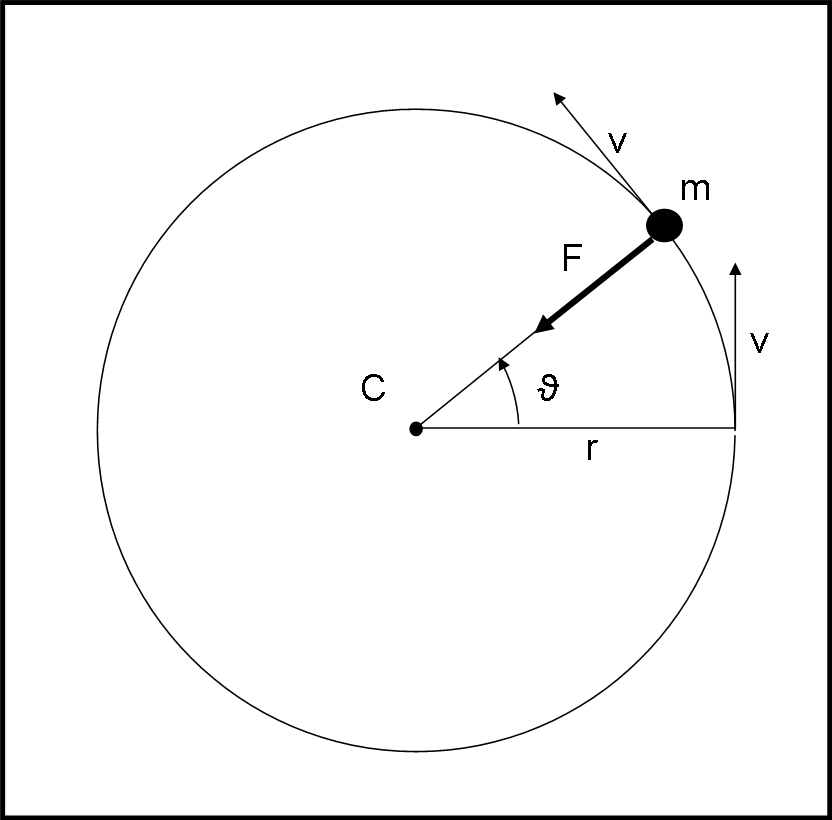
Per definire e descrivere il momento angolare e le sue proprietà è bene partire fin dall'inizio. Ed ecco che prima di arrivare a lui facciamo la conoscenza dei vettori, delle loro operazioni, della quantità di moto e dei principi della dinamica: una specie di riassunto di gran parte della dinamica classica. Senza dimenticare, ovviamente, la conservazione della quantità di moto e del suo figliolo momento angolare. Per far ciò useremo qualche colpo di scherma, un po' di Divina Commedia, qualche vite e/o qualche mano destra. Infine, mediante l'applicazione del momento angolare a un sistema particolare, introdurremo la dinamica dei moti circolari che imitano quasi perfettamente quelli traslatori o lineari.
Questo quiz non merita spiegazioni supplementari, dato che si risolve attraverso le regole descritte nei primi due capitoli dedicati al momento angolare, in cui si introducono i vettori, le loro operazioni e l’uso dei versori.
Finalmente richiamiamo i vettori e le loro caratteristiche. Siamo sempre nel campo della cinematica e, quindi, non c’è bisogno di energia. Rileggetevi i primi capitoli sul momento angolare…
In questo articolo ce n’è per tutti i gusti, come si vede dai vari gruppi di asterischi (difficoltà). La parte fondamentale, fino alla … “mano destra”, è abbastanza semplice e deve essere digerita da tutti coloro che vogliono andare avanti. Poi si passa a un piccolo esercizio e allo sviluppo attraverso le componenti (un piacere “estetico” non obbligatorio). Infine, chi non si accontenta ancora, può divertirsi con due vettori posti su un piano qualsiasi. In ogni modo, ho usato una trattazione piuttosto diversa dal solito che permette di spiare all’interno del mondo della dinamica rotatoria, dove il momento angolare ha un posto di primo piano.
Rimaniamo sempre tra i vettori, ma iniziamo a studiare il loro prodotto. Dato che i vettori sono grandezze veramente speciali non si accontentano di un solo prodotto, ma ne pretendono due. Cominciamo con quello “scalare”. Ci faremo aiutare dal grande Cyrano de Bergerac: “ed al fin della licenza io tocco!”
Cominciamo da lontano, ossia proprio dagli inizi. Per potere parlare di momento angolare bisogna prima conoscere molto bene cosa sono le grandezze fisiche e quali sono le operazioni che possono fare. In particolare, quelle relative ai vettori. Qualcuna la conosciamo già, ma le altre sono ancora abbastanza misteriose... Come faccio spesso, l'articolo si conclude con un piccolo esercizio che vi assicurerà di aver capito i concetti principali.