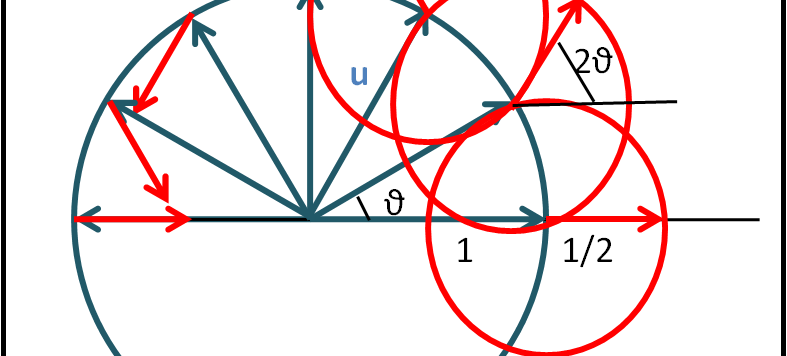
Prendiamoci un attimo di respiro e mostriamo una simpatica (e utile) visualizzazione della serie di Fourier tramite la rotazione di più vettori.
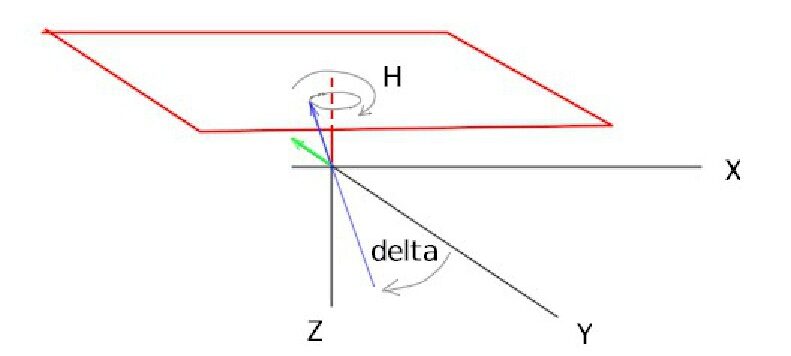
Eseguendo una sequenza di rotazioni si ottengono risultati diversi a seconda dell'ordine in cui si succedono le rotazioni. Occorre quindi operare una scelta, non casuale, al fine di ottenere la configurazione adatta al problema da risolvere.
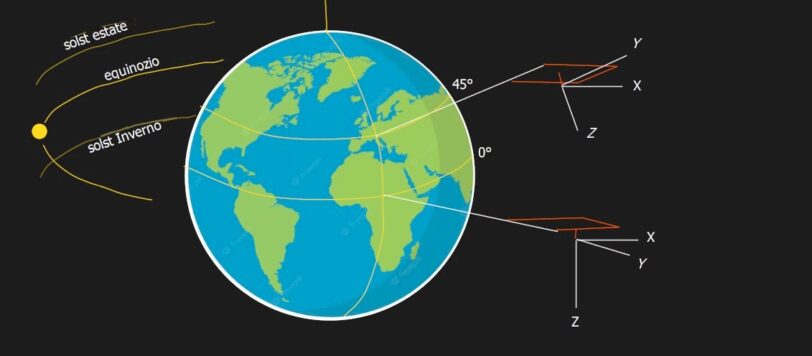
Le matrici di rotazione possono trovano una originale applicazione nel tracciamento delle curve di una meridiana.
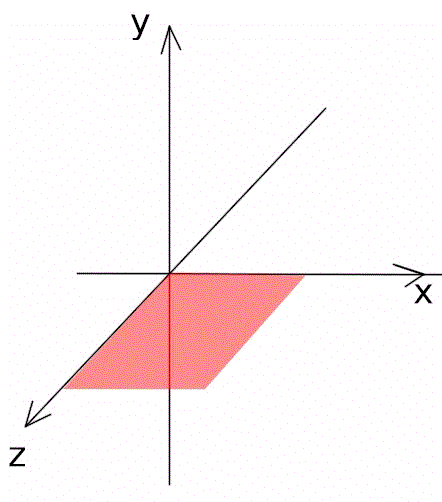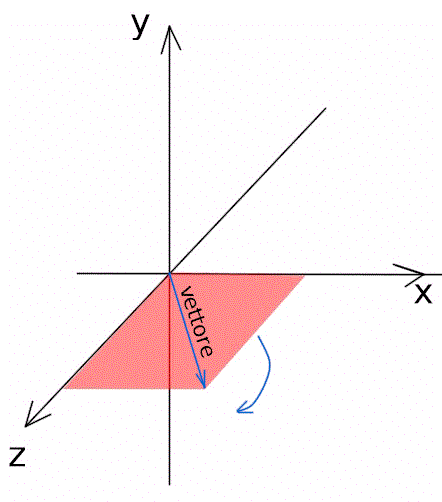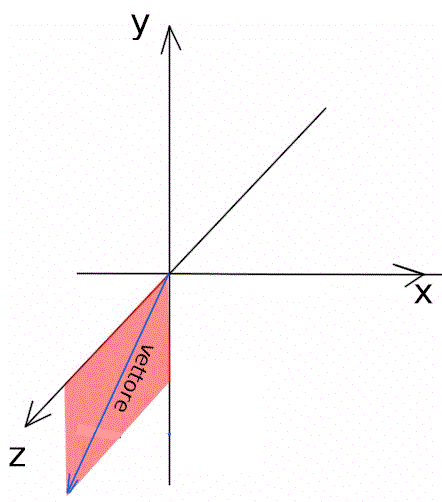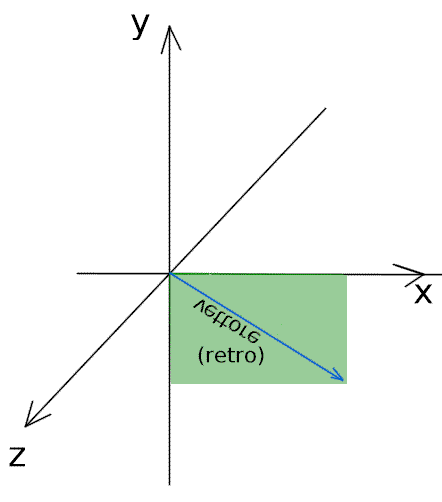
Questo articolo si propone di fornire un semplice strumento per rappresentare il meccanismo della rotazione in forma vettoriale, scomponendo e semplificando il problema di determinare i cambiamenti di orientamento dovuti a spostamenti rotatori.
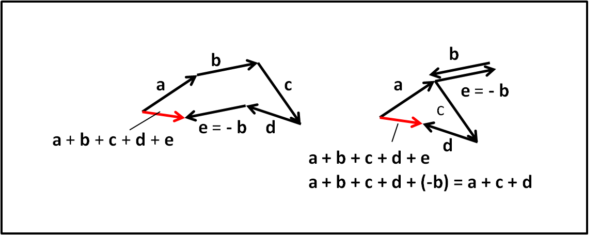
Questo articolo è decisamente elementare e descrive qualche "ovvia" proprietà della somma di vettori. Lo scopo finale, però, va oltre una semplice descrizione, dato che permette di avere le basi per affrontare un teorema poco noto, ma decisamente interessante. Un modo per evidenziare come la matematica e la geometria siano materie tutt'altro che aride e prive di emozioni.
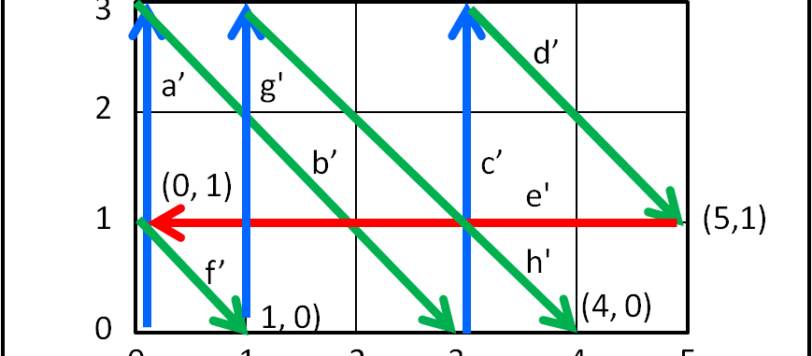
Il facile quiz sulle taniche da 5 e 3 litri è stato risolto brillantemente da Papalscherzone, ma mi ha fatto venire in mente un modo diverso per arrivare alla conclusione. Tra non molto ci divertiremo con i vettori e allora perché non usarli anche in questo caso?
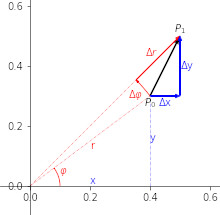
La domanda 2 del precedente articolo è un poco più difficile delle altre poiché richiede il calcolo di alcune derivate non banali.
Descrivo qui i passaggi in modo che chi li ha portati a termine possa confrontare la soluzione trovata e chi non è riuscito ad arrivare in fondo possa avere un aiuto.
In questo articolo propongo alcune domande ed alcuni approfondimenti sulle trasformazioni dei vettori trattate nell'articolo La Relatività Generale al microscopio. 4: I Tensori **. Cerco anche di collegare i vettori e le loro trasformazioni con le entità trattate negli articoli precedenti. In particolare scalari (tensori di rango 0) e gradienti.
Proseguo con le descrizione di alcuni fatti sperimentali. L'obiettivo è arrivare alla relazione che lega la polarizzazione dei fotoni entranti in un cristallo polarizzatore con le frazioni di fotoni rivelati dai due contatori all'uscita del cristallo. La relazione è nota come legge di Malus. In appendice c'è anche una breve introduzione ai vettori.
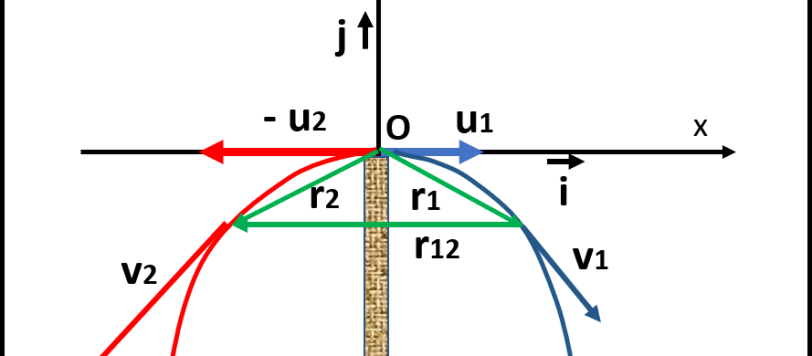
Un problema che si risolve molto elegantemente lavorando solo con i vettori (e i versori), ricordando una classica operazione tra di loro.
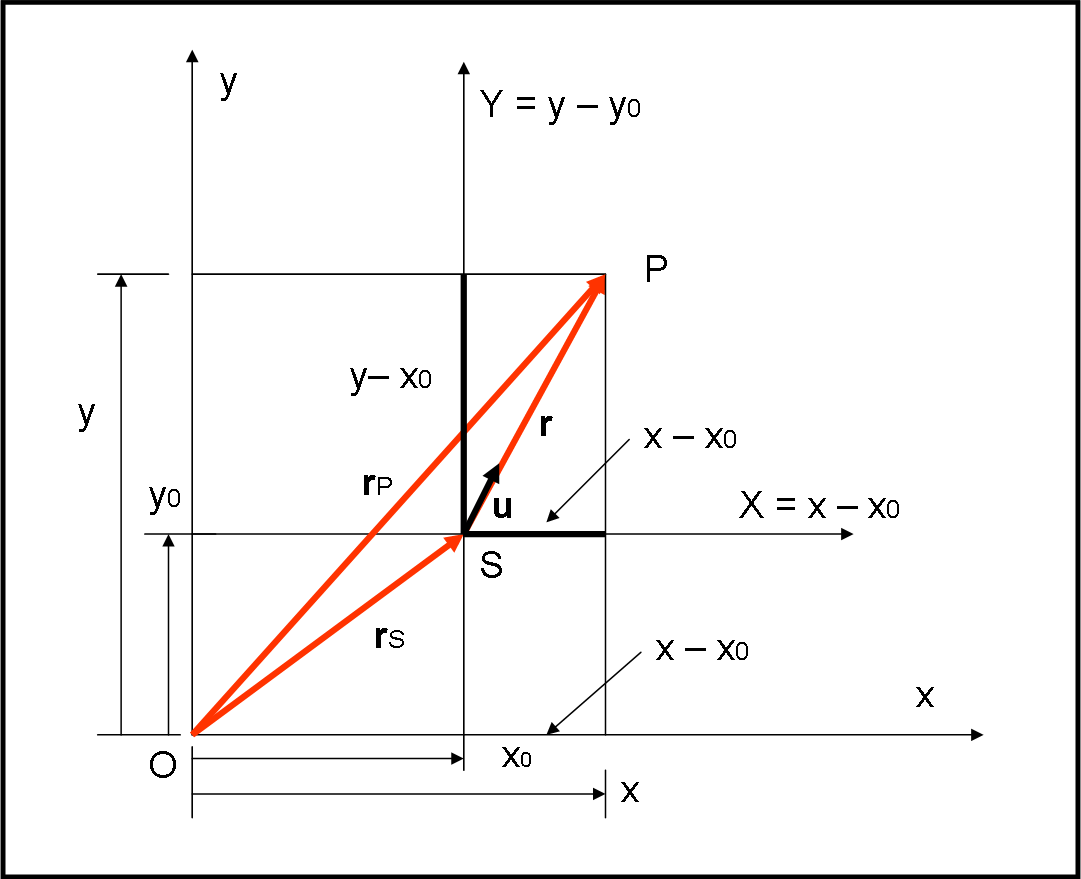
Dedichiamoci al problema più “difficile”, ossia a quello di ricavare il moto ellittico partendo dalla leggi di Newton. Ci accorgeremo che prima di arrivare alla fine, incontreremo già la seconda legge di Keplero, oltre che fare amicizia con un piano. In questa prima parte ci fermeremo proprio su questo piano. Procediamo con molta lentezza e chiarezza. Alla fine il moto orbitale avrà ben pochi segreti...
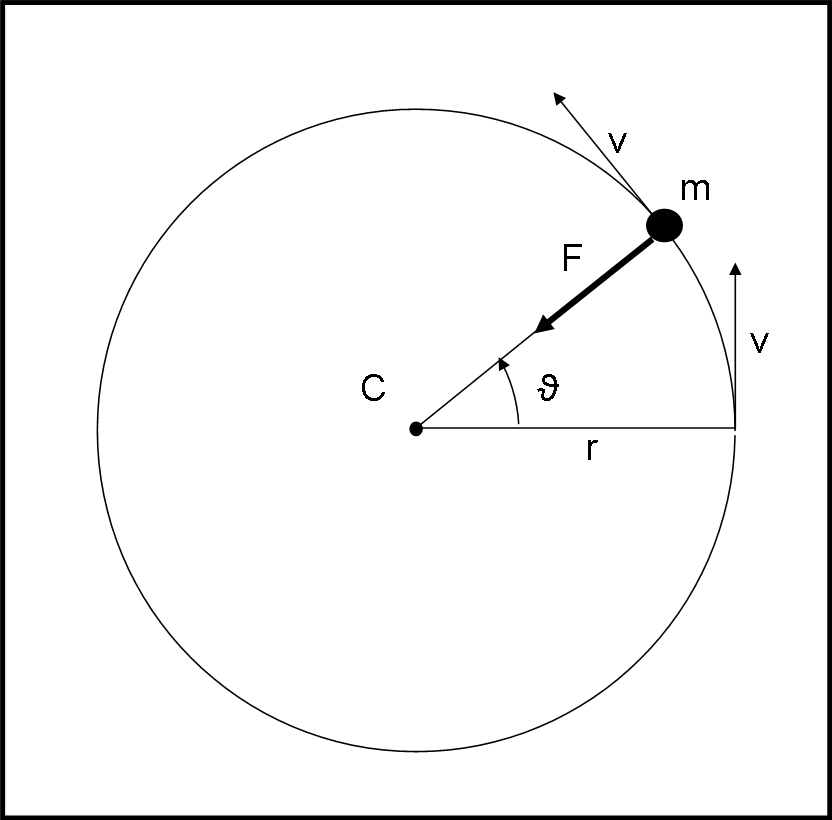
Per definire e descrivere il momento angolare e le sue proprietà è bene partire fin dall'inizio. Ed ecco che prima di arrivare a lui facciamo la conoscenza dei vettori, delle loro operazioni, della quantità di moto e dei principi della dinamica: una specie di riassunto di gran parte della dinamica classica. Senza dimenticare, ovviamente, la conservazione della quantità di moto e del suo figliolo momento angolare. Per far ciò useremo qualche colpo di scherma, un po' di Divina Commedia, qualche vite e/o qualche mano destra. Infine, mediante l'applicazione del momento angolare a un sistema particolare, introdurremo la dinamica dei moti circolari che imitano quasi perfettamente quelli traslatori o lineari.
Questo quiz non merita spiegazioni supplementari, dato che si risolve attraverso le regole descritte nei primi due capitoli dedicati al momento angolare, in cui si introducono i vettori, le loro operazioni e l’uso dei versori.
Finalmente richiamiamo i vettori e le loro caratteristiche. Siamo sempre nel campo della cinematica e, quindi, non c’è bisogno di energia. Rileggetevi i primi capitoli sul momento angolare…
Rimaniamo sempre tra i vettori, ma iniziamo a studiare il loro prodotto. Dato che i vettori sono grandezze veramente speciali non si accontentano di un solo prodotto, ma ne pretendono due. Cominciamo con quello “scalare”. Ci faremo aiutare dal grande Cyrano de Bergerac: “ed al fin della licenza io tocco!”
Cominciamo da lontano, ossia proprio dagli inizi. Per potere parlare di momento angolare bisogna prima conoscere molto bene cosa sono le grandezze fisiche e quali sono le operazioni che possono fare. In particolare, quelle relative ai vettori. Qualcuna la conosciamo già, ma le altre sono ancora abbastanza misteriose... Come faccio spesso, l'articolo si conclude con un piccolo esercizio che vi assicurerà di aver capito i concetti principali.